Browse By Unit
3.3 Differentiating Inverse Functions
Welcome back to AP Calculus with Fiveable! This topic focuses on differentiating inverse functions given equations or values. We’ve worked through chain rule and implicit differentiation, so let's keep building our derivative skills. 🙌
🔁 Differentiating Inverse Functions
If is the inverse of , a differentiable and invertible function, then the derivative of the inverse function can be found using this formula:
This can also be simplified into the following formula if is the inverse of :
We can remember this rule by saying “the derivative of the inverse is the reciprocal of the derivative.” This is because if , . If you need some more practice with inverse functions, review this Fiveable Guide: Inverse Functions.
Check out the visual below! We can see that the slopes of the function and its inverse are reciprocals of one another at the point . 🤩

Graph created with Desmos
🧮 Practice Problems
Let’s work on a few questions and make sure we have the concept down!
1) Calculating the Inverse Function
If , find .
To calculate , which equals , we need to first calculate . We can solve for by switching variables and solving for y.
Switching variables would make become . Let’s simplify this further…
Now that we have the inverse function, we can solve for by plugging into it.
Great! We calculated , now we can differentiate this value using our equation. Let’s plug in.
Next, we need to solve for . We can conclude that so also .
Let's finish solving using the equation.
Excellent work! 👏
2) Inverse Function Values from a Table
The following free-response question (FRQ) is from the 2007 AP Calculus AB examination administered by College Board. All credit to College Board.
The functions and are differentiable for all real numbers, and is strictly increasing. The table below gives values of the functions and their first derivatives at selected values of .
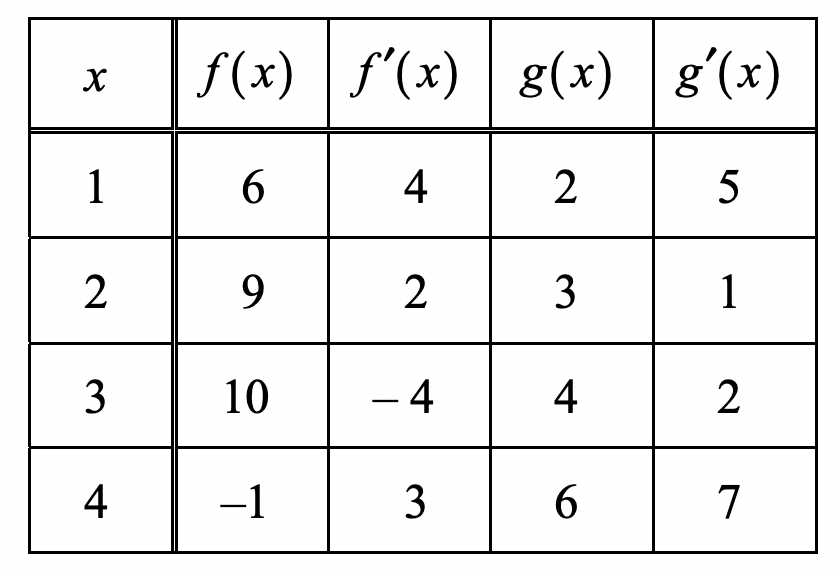
2007 AP Calculus AB examination
If is the inverse function of g, write an equation for the line tangent to the graph of at .
a. Find the slope of the tangent line at
We are looking for a line tangent to for this question.
At , the value of is not directly given. But the corresponding point on the function is must . Since , we can conclude that . We can now use the equation to solve for !
Therefore,
b. Write the equation of the tangent line
To write the equation of the line tangent to the graph of at , we will need to plug into this formula: .
We just calculated the value of , which equals . We know that , and found that
We can just plug it into the equation now! We can now answer that .
Amazing job! Our answers would have earned 3/3 points for this question. This one was tough since we had three different functions to look at: and , and had to take the calculations a step further. 🎉
🌟 Closing
Great work! 🙌 Differentiating inverse functions is a key foundational idea for AP Calculus. You can anticipate encountering questions involving differentiating inverse functions on the exam, both in multiple-choice and as part of a free response.

Image Courtesy of Giphy
<< Hide Menu
3.3 Differentiating Inverse Functions
Welcome back to AP Calculus with Fiveable! This topic focuses on differentiating inverse functions given equations or values. We’ve worked through chain rule and implicit differentiation, so let's keep building our derivative skills. 🙌
🔁 Differentiating Inverse Functions
If is the inverse of , a differentiable and invertible function, then the derivative of the inverse function can be found using this formula:
This can also be simplified into the following formula if is the inverse of :
We can remember this rule by saying “the derivative of the inverse is the reciprocal of the derivative.” This is because if , . If you need some more practice with inverse functions, review this Fiveable Guide: Inverse Functions.
Check out the visual below! We can see that the slopes of the function and its inverse are reciprocals of one another at the point . 🤩

Graph created with Desmos
🧮 Practice Problems
Let’s work on a few questions and make sure we have the concept down!
1) Calculating the Inverse Function
If , find .
To calculate , which equals , we need to first calculate . We can solve for by switching variables and solving for y.
Switching variables would make become . Let’s simplify this further…
Now that we have the inverse function, we can solve for by plugging into it.
Great! We calculated , now we can differentiate this value using our equation. Let’s plug in.
Next, we need to solve for . We can conclude that so also .
Let's finish solving using the equation.
Excellent work! 👏
2) Inverse Function Values from a Table
The following free-response question (FRQ) is from the 2007 AP Calculus AB examination administered by College Board. All credit to College Board.
The functions and are differentiable for all real numbers, and is strictly increasing. The table below gives values of the functions and their first derivatives at selected values of .

2007 AP Calculus AB examination
If is the inverse function of g, write an equation for the line tangent to the graph of at .
a. Find the slope of the tangent line at
We are looking for a line tangent to for this question.
At , the value of is not directly given. But the corresponding point on the function is must . Since , we can conclude that . We can now use the equation to solve for !
Therefore,
b. Write the equation of the tangent line
To write the equation of the line tangent to the graph of at , we will need to plug into this formula: .
We just calculated the value of , which equals . We know that , and found that
We can just plug it into the equation now! We can now answer that .
Amazing job! Our answers would have earned 3/3 points for this question. This one was tough since we had three different functions to look at: and , and had to take the calculations a step further. 🎉
🌟 Closing
Great work! 🙌 Differentiating inverse functions is a key foundational idea for AP Calculus. You can anticipate encountering questions involving differentiating inverse functions on the exam, both in multiple-choice and as part of a free response.

Image Courtesy of Giphy

© 2024 Fiveable Inc. All rights reserved.