Browse By Unit
2.8 Inverse Functions
A function is considered invertible (or “a function has an inverse function”) if it meets certain criteria: 🙃
1️⃣ The function must be a one-to-one function, which means that each output value of the function corresponds to a unique input value. This is often referred to as the "horizontal line test" where if a horizontal line intersects the graph of the function at more than one point, the function is not one-to-one and therefore not invertible.
2️⃣ Its domain must not be restricted in a way that would prevent the function from having an inverse. For example, if a function is defined only for a certain range of values, it may not be invertible because it does not cover the entire range of possible input values.
Additionally, inverse functions must also be defined on the range of the original function and the range of the inverse function is the domain of the original function.
✏️ Notation
If a function is invertible, the inverse function is denoted by f^-1. The inverse function is a reflection of the original function across the line y = x. 🪞
The domain of the inverse function is the range of the original function and the range of the inverse function is the domain of the original function.
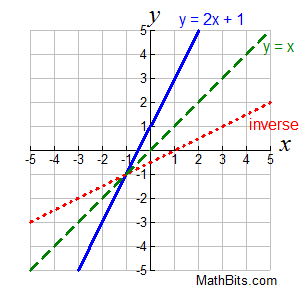
Source: MathBits.com
An inverse function can be thought of as the reverse or opposite of the original function. It takes the output values of the original function and maps them back to their corresponding input values. Essentially, it undoes the operation of the original function. 🔄
For example, if the original function f(x) = 2x, the inverse function f^-1(x) would be x/2. If we apply the original function to the input value of 2, we get an output value of 4. If we then apply the inverse function to the output value of 4, we get the original input value of 2. This is expressed mathematically as f(2) = 4 and f^-1(4) = 2
Another way to think about inverse functions is that they consist of input-output pairs that are flipped from the original function. The original function might have input-output pairs such as (2, 4), (3, 6), (4, 8), etc. The inverse function would have input-output pairs such as (4, 2), (6, 3), (8, 4), etc.
📝 Notes
- Not all functions have inverses, and a function is invertible only if it is one-to-one and its domain is not restricted. Additionally, an inverse function is only defined for the range of the original function. ⚔️
- The inverse function is not always a “function.” It can be multivalued, meaning that there can be multiple outputs for a given input. This happens when the original function is not one-to-one. In these cases, in order to make it a function, we need to restrict the domain of the original function in such a way that it becomes one-to-one.
🧐 Finding Inverse Functions (Given Original Function)
The most straightforward way to find the inverse of a function is to reverse the roles of x and y in the equation of the original function. This means that we switch the positions of x and y in the equation and make x the subject. 🔍
For example, if the original function is f(x) = 2x + 3, the inverse function can be found by reversing the roles of x and y:
y = 2x + 3
Switch: x = 2y + 3
To find the inverse function, we solve for y:
y = (x-3) / 2
So the inverse function is f^-1(x) = (x-3) / 2! ⭐
This method works for any function, as long as it is invertible. However, it's important to (again) note that not all functions have inverses. A function is invertible only if it is one-to-one and its domain is not restricted!
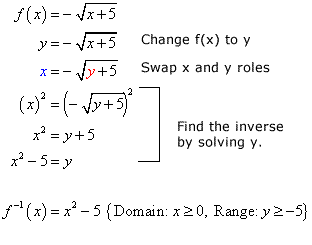
Source: ChiliMath
<< Hide Menu
2.8 Inverse Functions
A function is considered invertible (or “a function has an inverse function”) if it meets certain criteria: 🙃
1️⃣ The function must be a one-to-one function, which means that each output value of the function corresponds to a unique input value. This is often referred to as the "horizontal line test" where if a horizontal line intersects the graph of the function at more than one point, the function is not one-to-one and therefore not invertible.
2️⃣ Its domain must not be restricted in a way that would prevent the function from having an inverse. For example, if a function is defined only for a certain range of values, it may not be invertible because it does not cover the entire range of possible input values.
Additionally, inverse functions must also be defined on the range of the original function and the range of the inverse function is the domain of the original function.
✏️ Notation
If a function is invertible, the inverse function is denoted by f^-1. The inverse function is a reflection of the original function across the line y = x. 🪞
The domain of the inverse function is the range of the original function and the range of the inverse function is the domain of the original function.

Source: MathBits.com
An inverse function can be thought of as the reverse or opposite of the original function. It takes the output values of the original function and maps them back to their corresponding input values. Essentially, it undoes the operation of the original function. 🔄
For example, if the original function f(x) = 2x, the inverse function f^-1(x) would be x/2. If we apply the original function to the input value of 2, we get an output value of 4. If we then apply the inverse function to the output value of 4, we get the original input value of 2. This is expressed mathematically as f(2) = 4 and f^-1(4) = 2
Another way to think about inverse functions is that they consist of input-output pairs that are flipped from the original function. The original function might have input-output pairs such as (2, 4), (3, 6), (4, 8), etc. The inverse function would have input-output pairs such as (4, 2), (6, 3), (8, 4), etc.
📝 Notes
- Not all functions have inverses, and a function is invertible only if it is one-to-one and its domain is not restricted. Additionally, an inverse function is only defined for the range of the original function. ⚔️
- The inverse function is not always a “function.” It can be multivalued, meaning that there can be multiple outputs for a given input. This happens when the original function is not one-to-one. In these cases, in order to make it a function, we need to restrict the domain of the original function in such a way that it becomes one-to-one.
🧐 Finding Inverse Functions (Given Original Function)
The most straightforward way to find the inverse of a function is to reverse the roles of x and y in the equation of the original function. This means that we switch the positions of x and y in the equation and make x the subject. 🔍
For example, if the original function is f(x) = 2x + 3, the inverse function can be found by reversing the roles of x and y:
y = 2x + 3
Switch: x = 2y + 3
To find the inverse function, we solve for y:
y = (x-3) / 2
So the inverse function is f^-1(x) = (x-3) / 2! ⭐
This method works for any function, as long as it is invertible. However, it's important to (again) note that not all functions have inverses. A function is invertible only if it is one-to-one and its domain is not restricted!
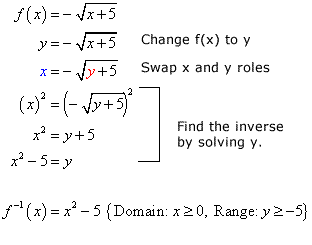
Source: ChiliMath

© 2024 Fiveable Inc. All rights reserved.