Browse By Unit
Dalia Savy
Dalia Savy
3.1 The Chain Rule
Welcome to the first key topic of Unit 3! In this key topic, we’ll learn more about taking derivatives of functions within functions, also known as composite functions. If you need a review on how to take derivatives, review Unit 2!
🔄 Composite Functions
Yep! Composite functions are functions within functions, but what does this mean?
Given two functions and , the composite function is formed by applying function to the output of function .
Mathematically, the composite function is expressed as:. You can basically think of as the “inner function” and as the “outer function.”
Composite Function Example
Let’s consider the following two functions:
If we’re taking a look at the composite function , we have to be able to identify the inner function and the outer function. Let’s do that now! ⬇️
- The function acts as the inner function. It takes , multiplies it by 3, and adds 1 to the result.
- The function acts as the outer function. It takes the output of and squares it.
Therefore, we can think of this example as the following:
Understanding how composite functions work is crucial in the chain rule. Now let’s get into it!
🔗 Definition of The Chain Rule
The Chain Rule is a method of differentiation, just like the Power Rule, Product Rule, and Quotient Rule from the previous unit. There are two notations for the Chain Rule.
Let’s go through each piece of this:
- represents the overall derivative you are trying to find.
- is your inner function.
- represents the derivative of the “outer” function with respect to the inner function.
- represents the derivative of the “inner” function with respect to .
The next notation will make this all clearer! 🙏🏿
As you can see, in order to take the derivative of the composite function, you are taking the derivative from the outside ⬅️ to the inside ➡️. This will repeat if there is another function within .
🪜Steps to Chain Rule
To help break the chain rule down, follow these steps:
- 🤔 Define your inner and outer functions.
- ⬅️ Take the derivative of the outer function only!
- ➡️ Take the derivative of the inner function with respect to .
- ✖️ Multiply the two derivatives to get your final answer!
Here’s a little graphic as well to help you visualize the chain rule.
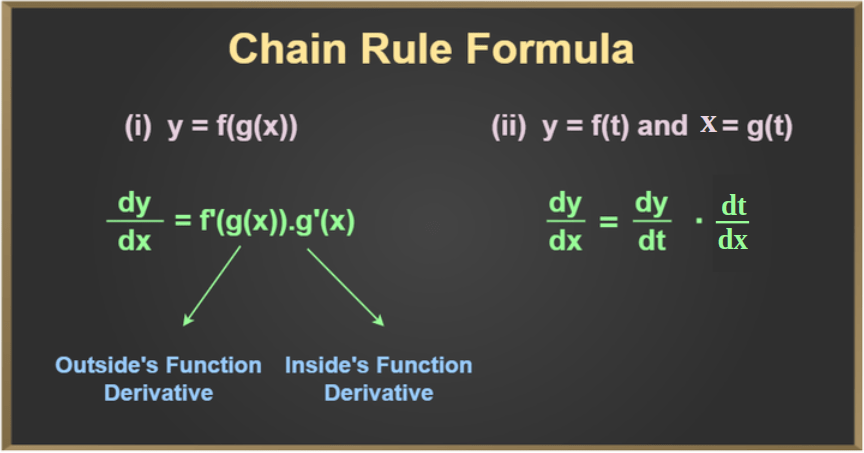
Image Courtesy of Geeks for Geeks
🔢 The Chain Rule: Practice Problems
The Chain Rule: Example 1
Find the derivative of the following function with respect to .
1️⃣ Define your inner and outer functions.
The inner function is . The outer function is .
2️⃣ Take the derivative of the outer function only!
As you can see, we have not taken the derivative of the inner function yet.
3️⃣ Take the derivative of the inner function with respect to .
4️⃣ Now multiply the two derivatives to get your final answer!
The Chain Rule: Example 2
Let and . Find the derivative of with respect to .
1️⃣ Define your inner and outer functions.
In this problem, they are more explicit! is the outer function and is the inner function.
2️⃣ Take the derivative of the outer function.
The derivative of is just !
3️⃣ Take the derivative of the inner function with respect to .
4️⃣ Then multiply the two derivatives to get your final answer!
The Chain Rule: Example 3
Find the derivative of the following function; this one may be a bit tougher!
1️⃣ Define your inner and outer functions.
The inner function is and the outer function is .
2️⃣ Take the derivative of the outer function.
3️⃣ Take the derivative of the inner function with respect to .
4️⃣ Now multiply the two derivatives to get your final answer!
The Chain Rule: Example 4
How about a function with a square root?
1️⃣ Define your inner and outer functions.
The inner function is and the outer function is .
2️⃣ Take the derivative of the outer function.
3️⃣ Take the derivative of the inner function with respect to .
4️⃣ Now multiply the two derivatives to get your final answer!
The Chain Rule: Example 5
Try taking the derivative of the following function yourself!
To help you out a little, the inner function is and the outer function is .
Here’s the answer:
📕 Closing
You made it through the first section of the unit! From now to the rest of your AP Calculus journey, the Chain Rule will accompany you and with practice, you will get to perfection! 🌟
<< Hide Menu
Dalia Savy
Dalia Savy
3.1 The Chain Rule
Welcome to the first key topic of Unit 3! In this key topic, we’ll learn more about taking derivatives of functions within functions, also known as composite functions. If you need a review on how to take derivatives, review Unit 2!
🔄 Composite Functions
Yep! Composite functions are functions within functions, but what does this mean?
Given two functions and , the composite function is formed by applying function to the output of function .
Mathematically, the composite function is expressed as:. You can basically think of as the “inner function” and as the “outer function.”
Composite Function Example
Let’s consider the following two functions:
If we’re taking a look at the composite function , we have to be able to identify the inner function and the outer function. Let’s do that now! ⬇️
- The function acts as the inner function. It takes , multiplies it by 3, and adds 1 to the result.
- The function acts as the outer function. It takes the output of and squares it.
Therefore, we can think of this example as the following:
Understanding how composite functions work is crucial in the chain rule. Now let’s get into it!
🔗 Definition of The Chain Rule
The Chain Rule is a method of differentiation, just like the Power Rule, Product Rule, and Quotient Rule from the previous unit. There are two notations for the Chain Rule.
Let’s go through each piece of this:
- represents the overall derivative you are trying to find.
- is your inner function.
- represents the derivative of the “outer” function with respect to the inner function.
- represents the derivative of the “inner” function with respect to .
The next notation will make this all clearer! 🙏🏿
As you can see, in order to take the derivative of the composite function, you are taking the derivative from the outside ⬅️ to the inside ➡️. This will repeat if there is another function within .
🪜Steps to Chain Rule
To help break the chain rule down, follow these steps:
- 🤔 Define your inner and outer functions.
- ⬅️ Take the derivative of the outer function only!
- ➡️ Take the derivative of the inner function with respect to .
- ✖️ Multiply the two derivatives to get your final answer!
Here’s a little graphic as well to help you visualize the chain rule.

Image Courtesy of Geeks for Geeks
🔢 The Chain Rule: Practice Problems
The Chain Rule: Example 1
Find the derivative of the following function with respect to .
1️⃣ Define your inner and outer functions.
The inner function is . The outer function is .
2️⃣ Take the derivative of the outer function only!
As you can see, we have not taken the derivative of the inner function yet.
3️⃣ Take the derivative of the inner function with respect to .
4️⃣ Now multiply the two derivatives to get your final answer!
The Chain Rule: Example 2
Let and . Find the derivative of with respect to .
1️⃣ Define your inner and outer functions.
In this problem, they are more explicit! is the outer function and is the inner function.
2️⃣ Take the derivative of the outer function.
The derivative of is just !
3️⃣ Take the derivative of the inner function with respect to .
4️⃣ Then multiply the two derivatives to get your final answer!
The Chain Rule: Example 3
Find the derivative of the following function; this one may be a bit tougher!
1️⃣ Define your inner and outer functions.
The inner function is and the outer function is .
2️⃣ Take the derivative of the outer function.
3️⃣ Take the derivative of the inner function with respect to .
4️⃣ Now multiply the two derivatives to get your final answer!
The Chain Rule: Example 4
How about a function with a square root?
1️⃣ Define your inner and outer functions.
The inner function is and the outer function is .
2️⃣ Take the derivative of the outer function.
3️⃣ Take the derivative of the inner function with respect to .
4️⃣ Now multiply the two derivatives to get your final answer!
The Chain Rule: Example 5
Try taking the derivative of the following function yourself!
To help you out a little, the inner function is and the outer function is .
Here’s the answer:
📕 Closing
You made it through the first section of the unit! From now to the rest of your AP Calculus journey, the Chain Rule will accompany you and with practice, you will get to perfection! 🌟

© 2024 Fiveable Inc. All rights reserved.