Browse By Unit
5.4 Using the First Derivative Test to Determine Relative (Local) Extrema
4 min read•june 18, 2024
5.4 Using the First Derivative Test to Determine Relative (Local) Extrema
Welcome back to Calculus with Fiveable! Let’s get into it.
Can the derivative of a function give us more information than just where the function increases or decreases? Yes, it can! In this study guide, we’ll learn how you can use the derivative of a function to determine its relative or local extrema.
🥇 First Derivative Test
We can use the First Derivative Test to determine the relative (local) extrema of a function. It states that if the derivative of a function changes from positive to negative at a point (which means that the function changes from increasing to decreasing at the point), then the function has a local or relative maximum at that point. If the derivative changes from negative to positive at a point (which means that the function changes from decreasing to increasing at the point), then the function has a local or relative minimum at that point.
The process of applying the First Derivative Test is similar to the process of finding the intervals where the function increases or decreases.
First, we need to find the critical points of the function. A critical point is a point where the derivative of the function is equal to 0 or is not defined. Once these points have been identified, we need to find the sign of the derivative of the function on either side of the critical point.
- If the derivative is positive on the left side of the critical point and negative on the right side, then the point is a local maximum. ⬆️
- If the derivative is negative on the left side of the critical point and positive on the right side, then the point is a local minimum. ⬇️
- If the derivative is positive on both sides or negative on both sides, then the function is either always increasing or always decreasing at that point, and there is no relative extremum. 📈
✏️ First Derivative Test Walkthrough
Let’s walk through an example together.
Consider the function . The derivative of this function is using the power rule. At , the derivative is equal to , which means that it is a critical point, and thus we should evaluate the function’s derivative on either side of the point.
Derivative on the Left Side (for )
To check the behavior of the function on the left, substitute a value less than 0 into . Let’s use
Now we know that the derivative is negative for
Derivative on the Right Side (for )
The process is similar here! Substitute a value greater than 0 into . Let’s plug in
The derivative is positive for .
First Derivative Test Walkthrough Conclusion
The derivative of the function is negative on the left side of the point and the derivative of the function is positive on the right side, so the point is a local minimum. ⬇️
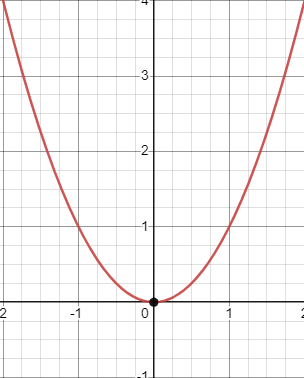
Image Created with Desmos
Take a look at the function and its local minimum!
📝 First Derivative Test Practice Problems
Now it’s time for you to do some practice on your own!
❓ First Derivative Test Problems
First Derivative Test Question 1:
Let be a polynomial function and let its derivative, , be defined as . Where are ’s relative minima?
First Derivative Test Question 2:
Let . Where are ’s relative maxima?
✅ First Derivative Test Solutions
First Derivative Test Question 1:
Since the problem asks us to find ’s relative minima, we should apply the First Derivative Test. To do so, we first find the function’s critical points by setting equal to
By solving each of these, we know that the critical points of are and . This means that the function can have minima at only these points.
Then we need to evaluate the left and right sides of the function’s derivative at each of these points to determine which are the relative minima. Here’s a table summarizing the results of plugging in the appropriate values!
| Left | Right | Verdict | |
| Relative maximum | |||
| Not an extremum | |||
| Relative minimum |
In conclusion, has one relative minimum at
First Derivative Test Question 2:
Since the problem asks us to find ’s relative maxima, we should apply the First Derivative Test. To do so, we first need to find the function’s critical points. Since , the critical points are and in this problem as are at these points. This means that the function can have maxima at only these points.
We then need to evaluate the left and right sides of the function’s derivative at each of these points to determine which are the relative maxima.
| Left | Right | Verdict | |
| Relative maximum | |||
| Relative minimum |
In conclusion, has one relative maximum at
🌟 Closing
Great work! The Derivative Test is a great tool that allows us to determine relative extrema of a function by identifying critical points and analyzing the sign of the derivative on either side of those points. It's important to keep in mind the limitations of the test and use other techniques to determine global extrema.
<< Hide Menu
5.4 Using the First Derivative Test to Determine Relative (Local) Extrema
4 min read•june 18, 2024
5.4 Using the First Derivative Test to Determine Relative (Local) Extrema
Welcome back to Calculus with Fiveable! Let’s get into it.
Can the derivative of a function give us more information than just where the function increases or decreases? Yes, it can! In this study guide, we’ll learn how you can use the derivative of a function to determine its relative or local extrema.
🥇 First Derivative Test
We can use the First Derivative Test to determine the relative (local) extrema of a function. It states that if the derivative of a function changes from positive to negative at a point (which means that the function changes from increasing to decreasing at the point), then the function has a local or relative maximum at that point. If the derivative changes from negative to positive at a point (which means that the function changes from decreasing to increasing at the point), then the function has a local or relative minimum at that point.
The process of applying the First Derivative Test is similar to the process of finding the intervals where the function increases or decreases.
First, we need to find the critical points of the function. A critical point is a point where the derivative of the function is equal to 0 or is not defined. Once these points have been identified, we need to find the sign of the derivative of the function on either side of the critical point.
- If the derivative is positive on the left side of the critical point and negative on the right side, then the point is a local maximum. ⬆️
- If the derivative is negative on the left side of the critical point and positive on the right side, then the point is a local minimum. ⬇️
- If the derivative is positive on both sides or negative on both sides, then the function is either always increasing or always decreasing at that point, and there is no relative extremum. 📈
✏️ First Derivative Test Walkthrough
Let’s walk through an example together.
Consider the function . The derivative of this function is using the power rule. At , the derivative is equal to , which means that it is a critical point, and thus we should evaluate the function’s derivative on either side of the point.
Derivative on the Left Side (for )
To check the behavior of the function on the left, substitute a value less than 0 into . Let’s use
Now we know that the derivative is negative for
Derivative on the Right Side (for )
The process is similar here! Substitute a value greater than 0 into . Let’s plug in
The derivative is positive for .
First Derivative Test Walkthrough Conclusion
The derivative of the function is negative on the left side of the point and the derivative of the function is positive on the right side, so the point is a local minimum. ⬇️

Image Created with Desmos
Take a look at the function and its local minimum!
📝 First Derivative Test Practice Problems
Now it’s time for you to do some practice on your own!
❓ First Derivative Test Problems
First Derivative Test Question 1:
Let be a polynomial function and let its derivative, , be defined as . Where are ’s relative minima?
First Derivative Test Question 2:
Let . Where are ’s relative maxima?
✅ First Derivative Test Solutions
First Derivative Test Question 1:
Since the problem asks us to find ’s relative minima, we should apply the First Derivative Test. To do so, we first find the function’s critical points by setting equal to
By solving each of these, we know that the critical points of are and . This means that the function can have minima at only these points.
Then we need to evaluate the left and right sides of the function’s derivative at each of these points to determine which are the relative minima. Here’s a table summarizing the results of plugging in the appropriate values!
| Left | Right | Verdict | |
| Relative maximum | |||
| Not an extremum | |||
| Relative minimum |
In conclusion, has one relative minimum at
First Derivative Test Question 2:
Since the problem asks us to find ’s relative maxima, we should apply the First Derivative Test. To do so, we first need to find the function’s critical points. Since , the critical points are and in this problem as are at these points. This means that the function can have maxima at only these points.
We then need to evaluate the left and right sides of the function’s derivative at each of these points to determine which are the relative maxima.
| Left | Right | Verdict | |
| Relative maximum | |||
| Relative minimum |
In conclusion, has one relative maximum at
🌟 Closing
Great work! The Derivative Test is a great tool that allows us to determine relative extrema of a function by identifying critical points and analyzing the sign of the derivative on either side of those points. It's important to keep in mind the limitations of the test and use other techniques to determine global extrema.

© 2024 Fiveable Inc. All rights reserved.