Browse By Unit
5.2 Extreme Value Theorem, Global vs Local Extrema, and Critical Points
6 min read•june 18, 2024
5.2 Extreme Value Theorem, Global vs Local Extrema, and Critical Points
Welcome back to AP Calculus with Fiveable! This topic focuses on extrema in an interval. Let’s dive right into the world of extreme values, both global and local, and the crucial concept of critical points. 🙌
🎢 Extreme Value Theorem
Let's start with the Extreme Value Theorem. The College Board AP Calculus Exam description states that a function defined on a closed interval must have both a maximum and minimum value within that interval. This is known as the Extreme Value Theorem, and it holds true if the function is continuous over the given interval . Check out this Fiveable guide to review continuity: Confirming Continuity over an Interval.
Check out the graph below. On the interval , there is one minimum value at , another at , and a maximum value at some point between and . It is okay for the minimum or maximum value to be at an end point, in fact, is is expected and something we need to check for!
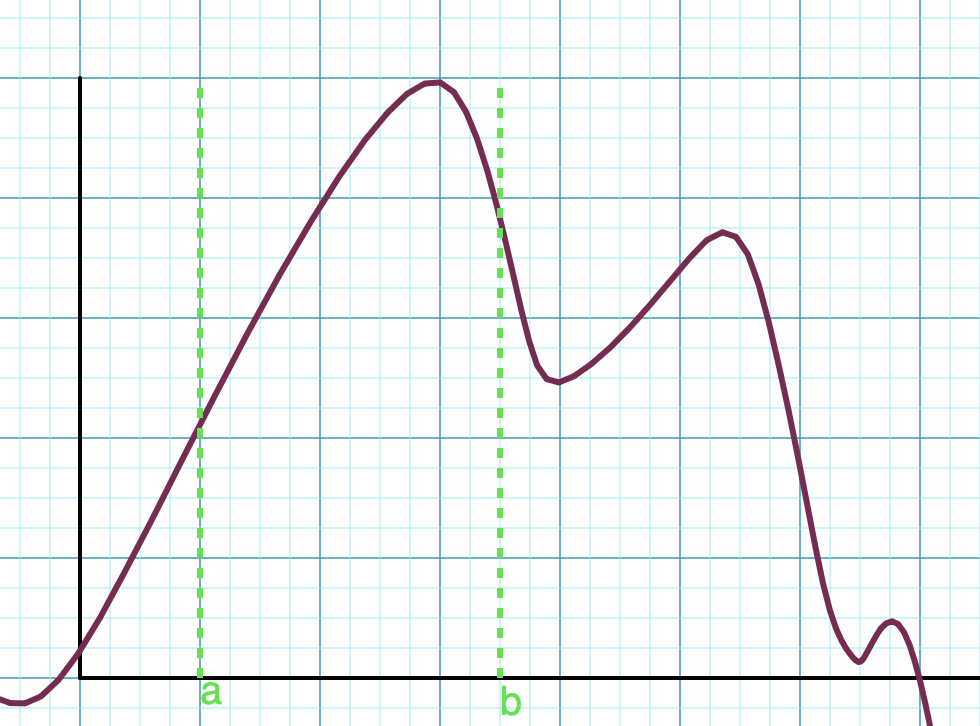
Graph created with Virtual Graph Paper
To apply this theorem effectively, think of the function as a roller coaster. As long as the roller coaster is continuous without any breaks or disruptions (discontinuities), you can expect it to have both a highest peak (maximum) and a lowest dip (minimum) somewhere along the ride. 🎢
🌐 Global Versus Local Extrema
Now, let's explore the difference between global and local extrema. Global extrema are the absolute maximum and minimum values of a function over its entire domain. We can identify these points because they are the absolute highest or lowest points when considering the function as a whole.
📍 Local extrema, on the other hand, focus on specific regions or intervals within the function. These points might not be the absolute highest or lowest in the entire domain but are the peaks and valleys within localized sections. We can identify these points if they are a maximum or minimum relative to the values directly surrounding them.
Take a look at this image below and try to identify all extrema as local or absolute and maximums or minimums on the interval .
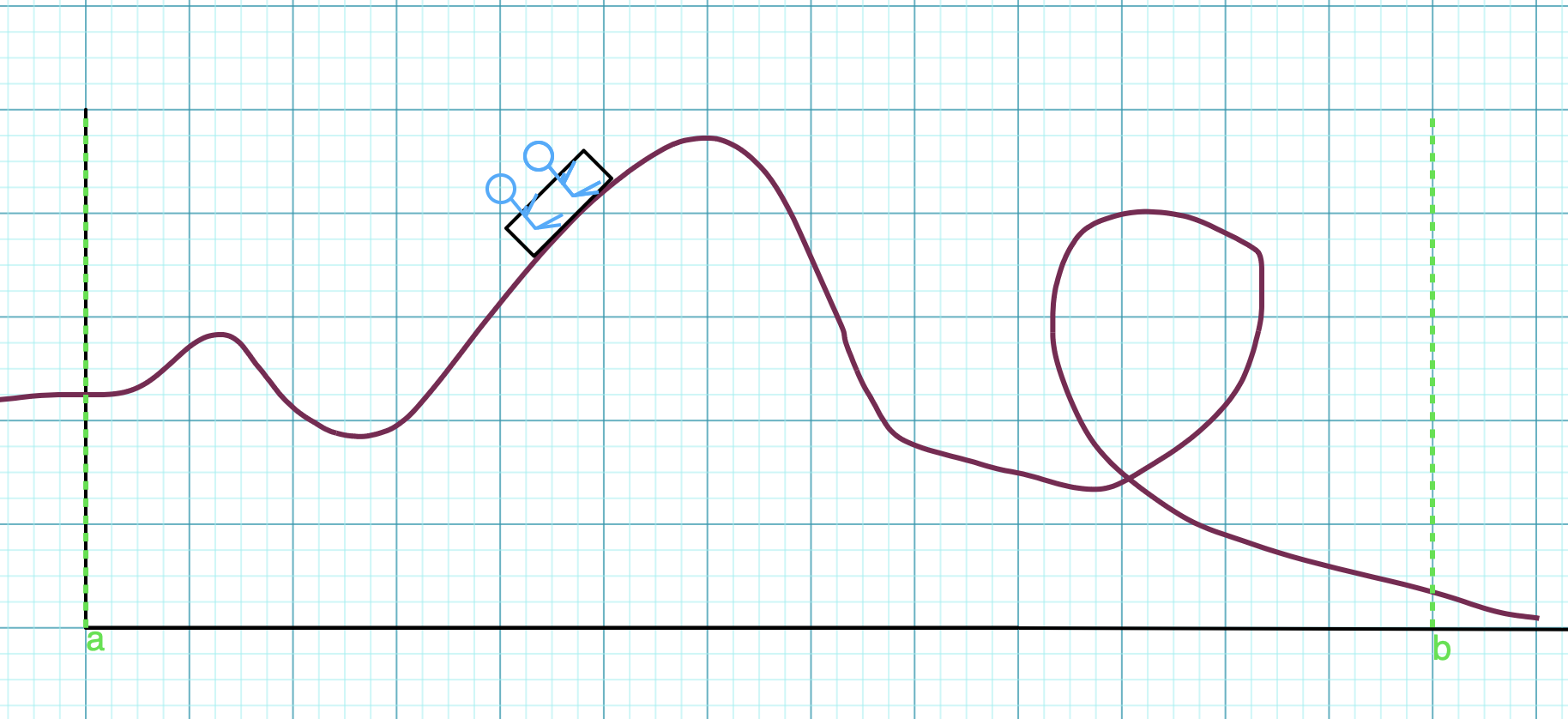
Graph created with Virtual Graph Paper
Using the Extreme Value Theorem, we can conclude that there must be one absolute maximum and one absolute minimum value on the interval since the function is continuous at all points.
Additionally, there are a few other points that qualify as local extrema because they are higher or lower than the points surrounding them. Consider if those points would also qualify as global extrema.
Let’s check that our points match with the ones marked below:
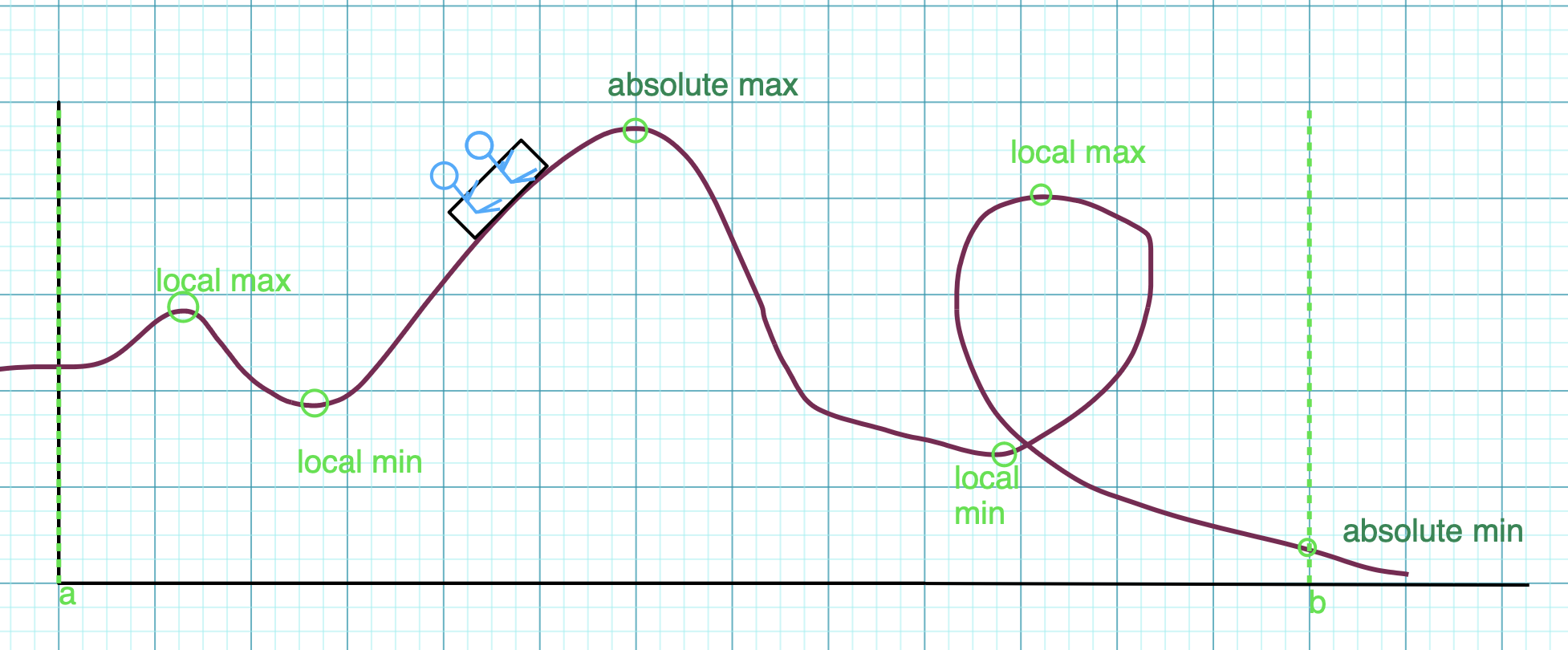
Graph created with Virtual Graph Paper
Great work!👍
🎯 Critical Points
Critical points play a pivotal role in identifying where extrema can occur. A critical point is a value in the domain of a function where the function is either not differentiable or its derivative is equal to zero: .
Think of critical points as potential tipping points on our roller coaster. At these points, the roller coaster may momentarily pause, change direction, or even come to a standstill. These critical points become the candidates for both local maxima and minima.
Look at the graph below. All of its extrema are critical points, but not all critical points are extrema! Point is a critical point since the derivative of the function at is 0, but it is not a local maximum or minimum.
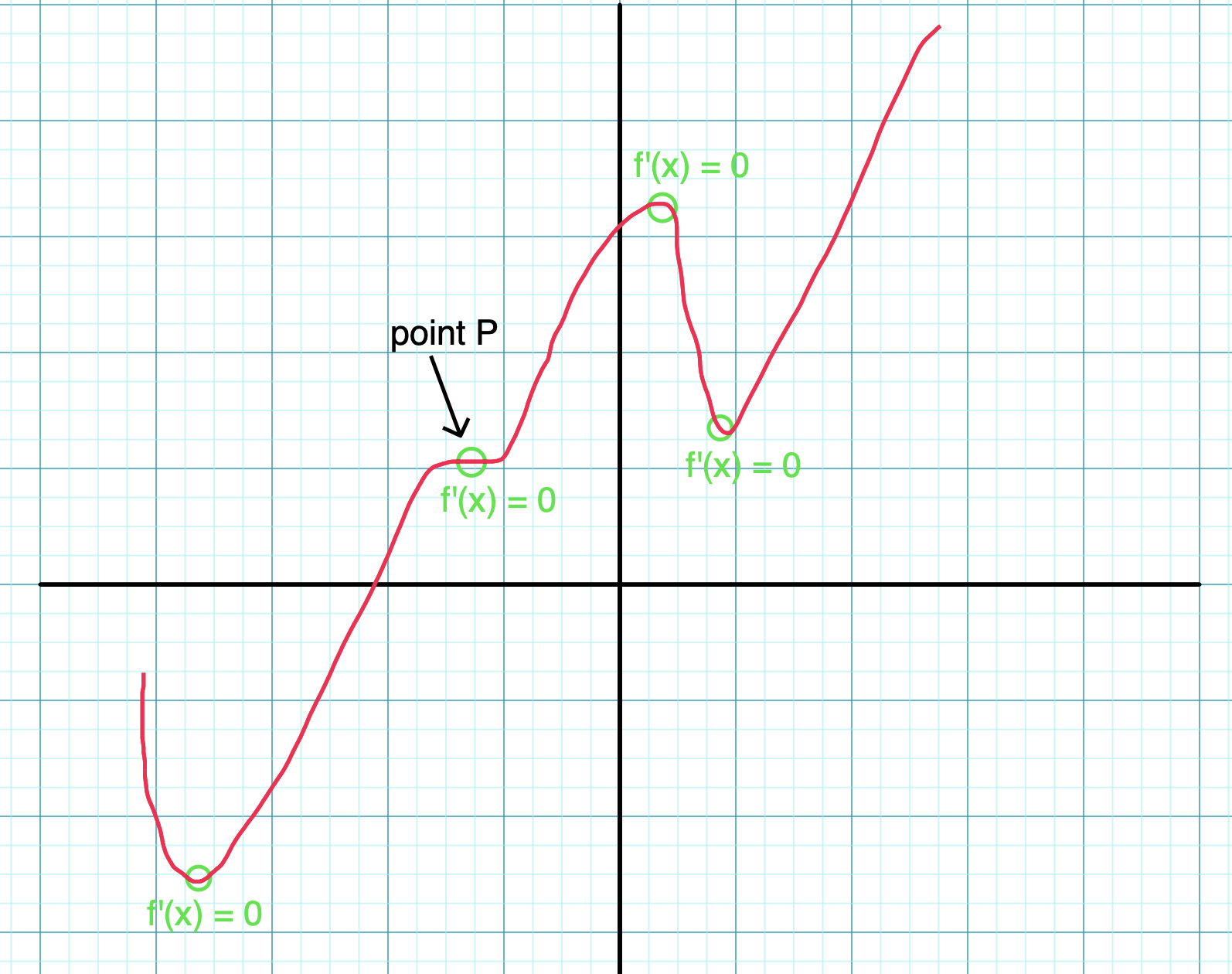
Graph created with Virtual Graph Paper
🔍 To identify critical points:
- is equal to
- is undefined
From there, you can check the critical points to determine if the value qualifies as extrema. We will cover that in a later topic, so stay tuned!
🧮 Practice Problems
1) Identifying Critical Points from a graph
Given the graph of , what points of the function would be critical points on the interval ?
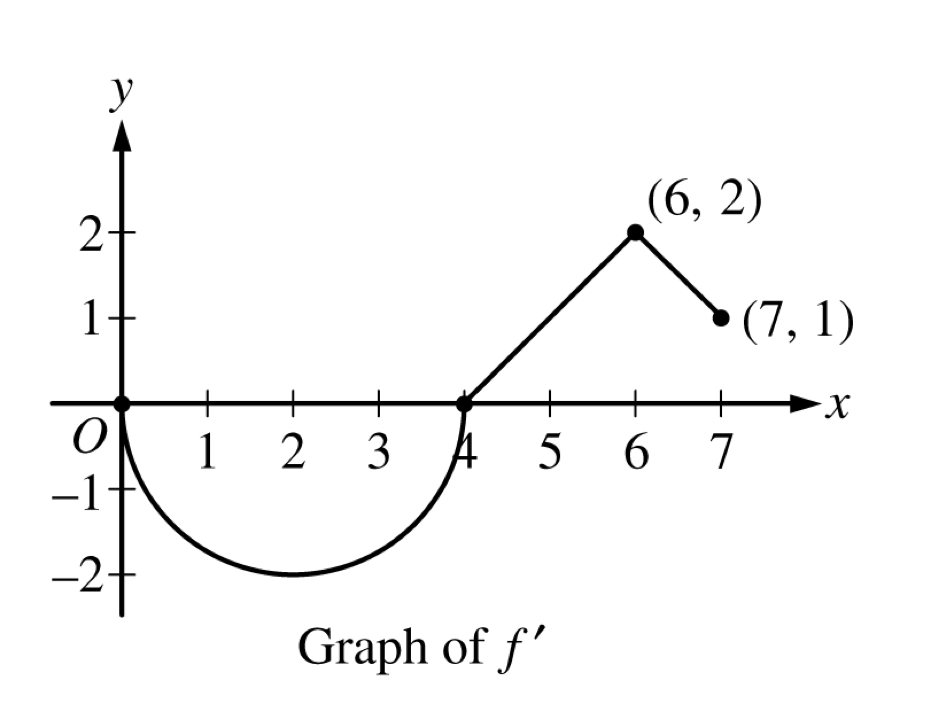
Graph from AP Calculus AB FRQ 2022. All credit to College Board
Let’s recall that at a critical point, the derivative either equals or does not exist. Therefore, we just have to check the graph of to see when it equals ! Since at and , we can conclude there are two critical points at and on the interval . You're on fire! 🔥
2) Identifying Extrema from a Graph
Given the graph of , identify if all critical points qualify as extrema, and identify an absolute maximum and minimum on the interval .
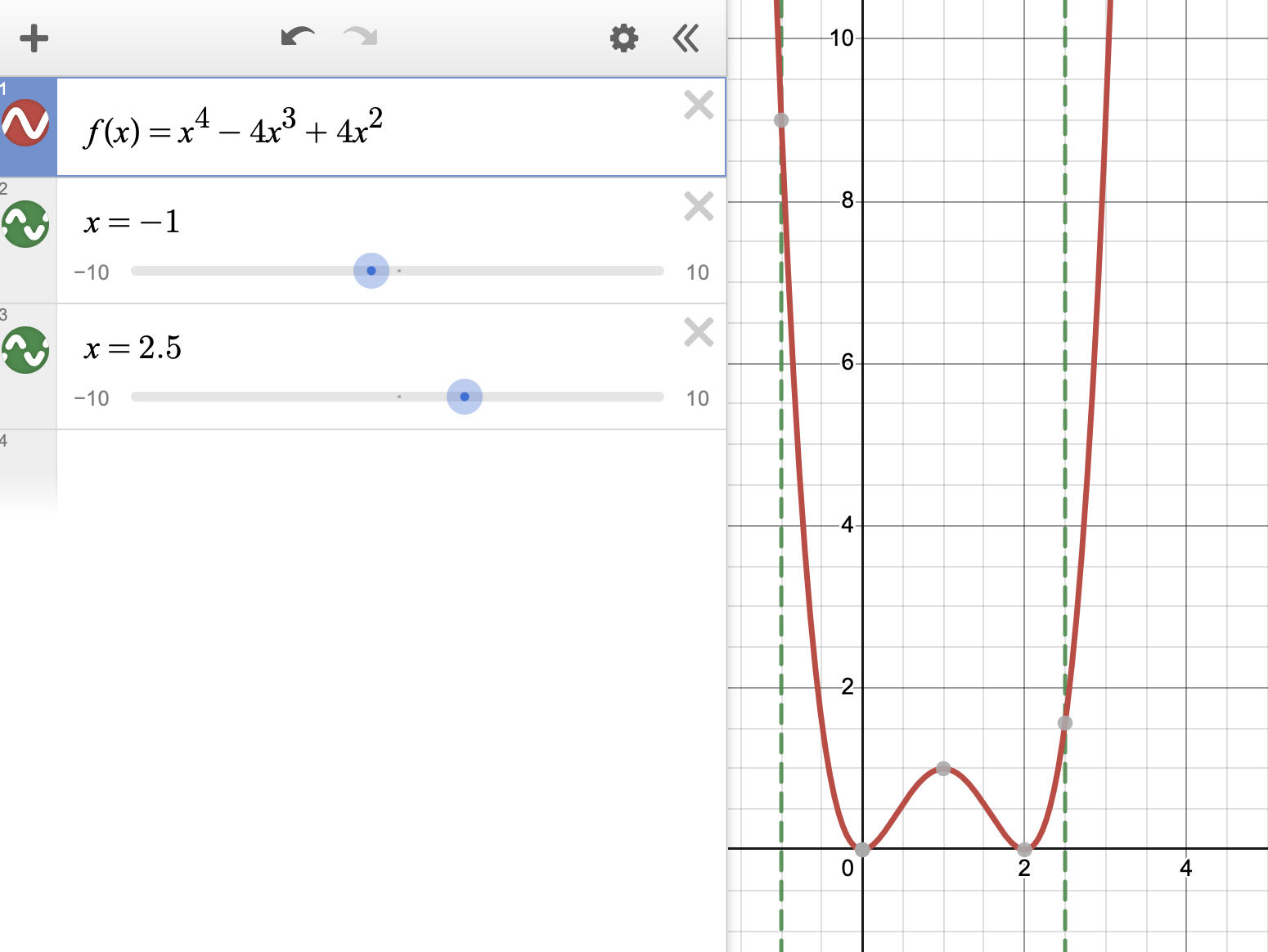
Graph created with Desmos
First, let's look at all of the critical points. At we have a local minimum since all surrounding points have a greater value. This is also the same for . Because these two points are also the lowest in the interval, and are absolute minimums.
Then, the other critical point is a local maximum since all of its surrounding values are lower.
Finally, we can take a look at the endpoints. The point must be the absolute maximum value of this function on the interval because it is higher than all of the other points in the interval. The point is only a local maximum, because it is higher than the points we can see in the interval. Nice job! 👍
3) Extreme Value Theorem
A function is defined as on the interval . Is the function guaranteed to have a maximum and minimum value in this interval?
Consider the requirements to apply the Extreme Value Theorem: the function must be continuous. However, the question does not supply the information that is continuous in the interval, or give us an equation to manually determine continuity. Therefore, we must conclude that the function is not guaranteed a maximum and minimum value on the interval .
🌟 Closing
Amazing work! 🙌 Understanding extreme values, global versus local extrema, and critical points is fundamental for tackling AP Calculus questions. You can anticipate encountering questions involving extrema and the Extreme Value Theorem on the exam, both in multiple-choice and as part of a free response.

Image Courtesy of Giphy
<< Hide Menu
5.2 Extreme Value Theorem, Global vs Local Extrema, and Critical Points
6 min read•june 18, 2024
5.2 Extreme Value Theorem, Global vs Local Extrema, and Critical Points
Welcome back to AP Calculus with Fiveable! This topic focuses on extrema in an interval. Let’s dive right into the world of extreme values, both global and local, and the crucial concept of critical points. 🙌
🎢 Extreme Value Theorem
Let's start with the Extreme Value Theorem. The College Board AP Calculus Exam description states that a function defined on a closed interval must have both a maximum and minimum value within that interval. This is known as the Extreme Value Theorem, and it holds true if the function is continuous over the given interval . Check out this Fiveable guide to review continuity: Confirming Continuity over an Interval.
Check out the graph below. On the interval , there is one minimum value at , another at , and a maximum value at some point between and . It is okay for the minimum or maximum value to be at an end point, in fact, is is expected and something we need to check for!

Graph created with Virtual Graph Paper
To apply this theorem effectively, think of the function as a roller coaster. As long as the roller coaster is continuous without any breaks or disruptions (discontinuities), you can expect it to have both a highest peak (maximum) and a lowest dip (minimum) somewhere along the ride. 🎢
🌐 Global Versus Local Extrema
Now, let's explore the difference between global and local extrema. Global extrema are the absolute maximum and minimum values of a function over its entire domain. We can identify these points because they are the absolute highest or lowest points when considering the function as a whole.
📍 Local extrema, on the other hand, focus on specific regions or intervals within the function. These points might not be the absolute highest or lowest in the entire domain but are the peaks and valleys within localized sections. We can identify these points if they are a maximum or minimum relative to the values directly surrounding them.
Take a look at this image below and try to identify all extrema as local or absolute and maximums or minimums on the interval .

Graph created with Virtual Graph Paper
Using the Extreme Value Theorem, we can conclude that there must be one absolute maximum and one absolute minimum value on the interval since the function is continuous at all points.
Additionally, there are a few other points that qualify as local extrema because they are higher or lower than the points surrounding them. Consider if those points would also qualify as global extrema.
Let’s check that our points match with the ones marked below:

Graph created with Virtual Graph Paper
Great work!👍
🎯 Critical Points
Critical points play a pivotal role in identifying where extrema can occur. A critical point is a value in the domain of a function where the function is either not differentiable or its derivative is equal to zero: .
Think of critical points as potential tipping points on our roller coaster. At these points, the roller coaster may momentarily pause, change direction, or even come to a standstill. These critical points become the candidates for both local maxima and minima.
Look at the graph below. All of its extrema are critical points, but not all critical points are extrema! Point is a critical point since the derivative of the function at is 0, but it is not a local maximum or minimum.

Graph created with Virtual Graph Paper
🔍 To identify critical points:
- is equal to
- is undefined
From there, you can check the critical points to determine if the value qualifies as extrema. We will cover that in a later topic, so stay tuned!
🧮 Practice Problems
1) Identifying Critical Points from a graph
Given the graph of , what points of the function would be critical points on the interval ?

Graph from AP Calculus AB FRQ 2022. All credit to College Board
Let’s recall that at a critical point, the derivative either equals or does not exist. Therefore, we just have to check the graph of to see when it equals ! Since at and , we can conclude there are two critical points at and on the interval . You're on fire! 🔥
2) Identifying Extrema from a Graph
Given the graph of , identify if all critical points qualify as extrema, and identify an absolute maximum and minimum on the interval .

Graph created with Desmos
First, let's look at all of the critical points. At we have a local minimum since all surrounding points have a greater value. This is also the same for . Because these two points are also the lowest in the interval, and are absolute minimums.
Then, the other critical point is a local maximum since all of its surrounding values are lower.
Finally, we can take a look at the endpoints. The point must be the absolute maximum value of this function on the interval because it is higher than all of the other points in the interval. The point is only a local maximum, because it is higher than the points we can see in the interval. Nice job! 👍
3) Extreme Value Theorem
A function is defined as on the interval . Is the function guaranteed to have a maximum and minimum value in this interval?
Consider the requirements to apply the Extreme Value Theorem: the function must be continuous. However, the question does not supply the information that is continuous in the interval, or give us an equation to manually determine continuity. Therefore, we must conclude that the function is not guaranteed a maximum and minimum value on the interval .
🌟 Closing
Amazing work! 🙌 Understanding extreme values, global versus local extrema, and critical points is fundamental for tackling AP Calculus questions. You can anticipate encountering questions involving extrema and the Extreme Value Theorem on the exam, both in multiple-choice and as part of a free response.

Image Courtesy of Giphy

© 2024 Fiveable Inc. All rights reserved.