Browse By Unit
4.7 Parametrization of Implicitly Defined Functions
1 min read•june 18, 2024
Jesse
Jesse
4.7 Parametrization of Implicitly Defined Functions
In 4.5, we introduced the idea of equations involving two variables being capable of implicitly defining one or more functions. Tying this concept to the rest of the first half of the unit, we’d like to know how to parametrize these types of functions! 🤔

Source: Nauman Umer
🏹 Representing Curves in Planes
A parametrization is a way to express a curve in the form of a set of equations x(t) and y(t) that depend on a parameter t. When these equations are substituted into the corresponding equation that defines the curve implicitly, they should satisfy the equation for every value of t in the domain. 🎢
For example, the equation x^2 + y^2 = 1 describes the unit circle centered at the origin. A parametrization of this circle is (x(t), y(t)) = (cos(t), sin(t)) with domain 0 < t < 2π. When we substitute these equations into the implicit equation we get cos(t)^2 + sin(t)^2 = 1 which is always true.
Moving on, if f is a function of x and y = f(x) is the graph of f, then the curve can be parametrized as (x(t), y(t)) = (t, f(t)) where x(t) = t and y(t) = f(t). This can be visualized as moving along the x-axis, starting at t = a and ending at t = b and at each point (t, f(t)) on the x-axis, the corresponding point (x, y) on the graph of f is plotted. 📈
When f is invertible, it means that the function has an inverse function, f^(-1), which is also a function of x. In this case, the inverse function can be parametrized as (x(t), y(t)) = (f(t), t) for an appropriate interval of t. This can be visualized as moving along the y-axis, starting at t = a and ending at t = b and at each point (f(t), t) on the y-axis, the corresponding point (x, y) on the graph of f^(-1) is plotted. ⏮
It's important to note that the domain of t for the inverse function will be the range of the original function! 🛼
🔔 Representing Conic Sections in Planes
In 4.6, we discussed conic sections, geometric shapes created by intersecting a plane and a cone, such as circles, ellipses, parabolas, and hyperbolas. Recall that each type of conic section can be defined by a specific equation and has its own unique properties. 👑
↪️ Parabolas
A parabola, like any other equation involving two variables, can be represented in a parametric form. One way to do this is to solve for one of the variables and express the other in terms of a parameter.
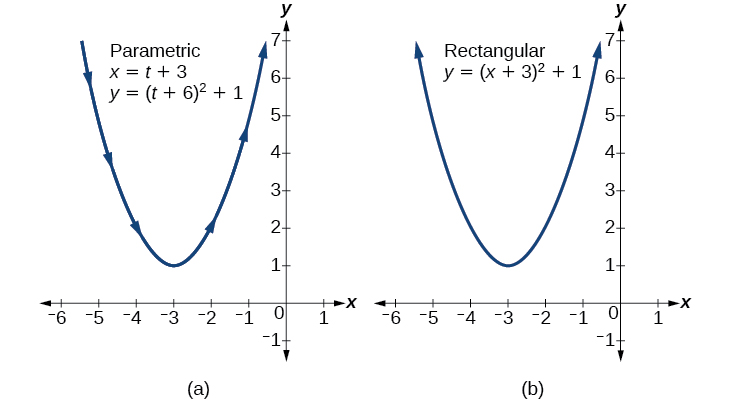
Source: Lumen Learning
For example, if the equation of the parabola can be solved for x, it can be parametrized as (x(t), y(t)) = (f(t), t), where x is expressed in terms of the parameter t and y is simply t. 🧐
Similarly, if the equation can be solved for y, it can be parametrized as (x(t), y(t)) = (t, f(t)), where y is now expressed in terms of t and x is t.
🥚 Ellipses
An ellipse can be represented in parametric form by the equations x(t) = h + acos(t) and y(t) = k + bsin(t) where h, k are the center coordinates of the ellipse, a and b are the semi-major and semi-minor axis respectively.
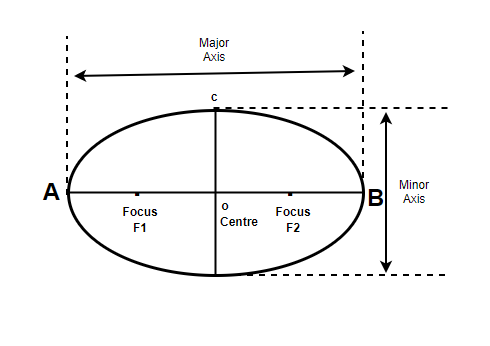
Source: Geeks for Geeks
The domain of the parametric equations is 0 ≤ t ≤ 2π, which represents a complete counterclockwise revolution of the ellipse. These equations use the trigonometric functions cosine and sine, which allow us to express the position of a point on the ellipse at any angle t, in terms of the distance from the center and the angle formed by the line segment joining the point on the ellipse to the center and the x-axis. 🕥
🔁 Hyperbolas
Recall that a hyperbola is a type of conic section that can be defined by its standard equation, (x^2/a^2) - (y^2/b^2) = 1, where a and b are the lengths of the semi-major and semi-minor axes of the hyperbola, respectively.
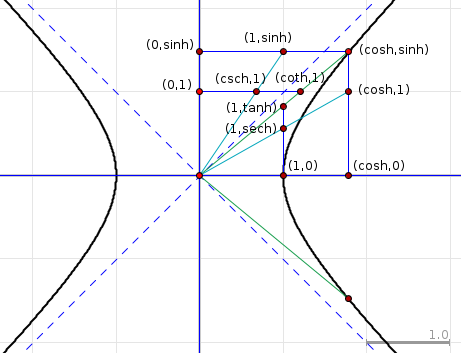
Source: Math Stack Exchange
For a hyperbola that opens horizontally, with the center located at the point (h, k), the parametric equations are given by: x(t) = h + a * sec(t) y(t) = k + b * tan(t), where t is the parameter, and a and b are the lengths of the semi-major and semi-minor axes, respectively. This representation is valid for 0 < t < 2π. ↔️
For a hyperbola that opens vertically, with the center located at the point (h, k), the parametric equations are given by: x(t) = h + a * tan(t) y(t) = k + b * sec(t), where t is the parameter, and a and b are the lengths of the semi-major and semi-minor axes, respectively. This representation is valid for 0 < t < 2π. ↕️
It's important to note that the functions sec(t) and tan(t) are the reciprocal functions of cos(t) and sin(t) respectively. ♣️
<< Hide Menu
4.7 Parametrization of Implicitly Defined Functions
1 min read•june 18, 2024
Jesse
Jesse
4.7 Parametrization of Implicitly Defined Functions
In 4.5, we introduced the idea of equations involving two variables being capable of implicitly defining one or more functions. Tying this concept to the rest of the first half of the unit, we’d like to know how to parametrize these types of functions! 🤔

Source: Nauman Umer
🏹 Representing Curves in Planes
A parametrization is a way to express a curve in the form of a set of equations x(t) and y(t) that depend on a parameter t. When these equations are substituted into the corresponding equation that defines the curve implicitly, they should satisfy the equation for every value of t in the domain. 🎢
For example, the equation x^2 + y^2 = 1 describes the unit circle centered at the origin. A parametrization of this circle is (x(t), y(t)) = (cos(t), sin(t)) with domain 0 < t < 2π. When we substitute these equations into the implicit equation we get cos(t)^2 + sin(t)^2 = 1 which is always true.
Moving on, if f is a function of x and y = f(x) is the graph of f, then the curve can be parametrized as (x(t), y(t)) = (t, f(t)) where x(t) = t and y(t) = f(t). This can be visualized as moving along the x-axis, starting at t = a and ending at t = b and at each point (t, f(t)) on the x-axis, the corresponding point (x, y) on the graph of f is plotted. 📈
When f is invertible, it means that the function has an inverse function, f^(-1), which is also a function of x. In this case, the inverse function can be parametrized as (x(t), y(t)) = (f(t), t) for an appropriate interval of t. This can be visualized as moving along the y-axis, starting at t = a and ending at t = b and at each point (f(t), t) on the y-axis, the corresponding point (x, y) on the graph of f^(-1) is plotted. ⏮
It's important to note that the domain of t for the inverse function will be the range of the original function! 🛼
🔔 Representing Conic Sections in Planes
In 4.6, we discussed conic sections, geometric shapes created by intersecting a plane and a cone, such as circles, ellipses, parabolas, and hyperbolas. Recall that each type of conic section can be defined by a specific equation and has its own unique properties. 👑
↪️ Parabolas
A parabola, like any other equation involving two variables, can be represented in a parametric form. One way to do this is to solve for one of the variables and express the other in terms of a parameter.

Source: Lumen Learning
For example, if the equation of the parabola can be solved for x, it can be parametrized as (x(t), y(t)) = (f(t), t), where x is expressed in terms of the parameter t and y is simply t. 🧐
Similarly, if the equation can be solved for y, it can be parametrized as (x(t), y(t)) = (t, f(t)), where y is now expressed in terms of t and x is t.
🥚 Ellipses
An ellipse can be represented in parametric form by the equations x(t) = h + acos(t) and y(t) = k + bsin(t) where h, k are the center coordinates of the ellipse, a and b are the semi-major and semi-minor axis respectively.

Source: Geeks for Geeks
The domain of the parametric equations is 0 ≤ t ≤ 2π, which represents a complete counterclockwise revolution of the ellipse. These equations use the trigonometric functions cosine and sine, which allow us to express the position of a point on the ellipse at any angle t, in terms of the distance from the center and the angle formed by the line segment joining the point on the ellipse to the center and the x-axis. 🕥
🔁 Hyperbolas
Recall that a hyperbola is a type of conic section that can be defined by its standard equation, (x^2/a^2) - (y^2/b^2) = 1, where a and b are the lengths of the semi-major and semi-minor axes of the hyperbola, respectively.

Source: Math Stack Exchange
For a hyperbola that opens horizontally, with the center located at the point (h, k), the parametric equations are given by: x(t) = h + a * sec(t) y(t) = k + b * tan(t), where t is the parameter, and a and b are the lengths of the semi-major and semi-minor axes, respectively. This representation is valid for 0 < t < 2π. ↔️
For a hyperbola that opens vertically, with the center located at the point (h, k), the parametric equations are given by: x(t) = h + a * tan(t) y(t) = k + b * sec(t), where t is the parameter, and a and b are the lengths of the semi-major and semi-minor axes, respectively. This representation is valid for 0 < t < 2π. ↕️
It's important to note that the functions sec(t) and tan(t) are the reciprocal functions of cos(t) and sin(t) respectively. ♣️

© 2024 Fiveable Inc. All rights reserved.