Browse By Unit
Jesse
Jesse
4.10 Matrices
A matrix is a rectangular array of numbers, symbols, or expressions that are arranged in rows ↔️ and columns. ↕️ Imagine a spreadsheet or a table with numbers arranged in rows and columns. This is similar to a matrix, but instead of being used for organizing data, matrices are used in mathematics to perform operations such as solving systems of equations, calculating determinants, and representing transformations. ⚙️
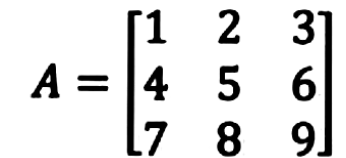
Source: StudyPug
You can also think of a matrix like a collection of different tools in a toolbox. Each tool has its own unique purpose, and you can use them to accomplish different tasks. 🔨
✍️ Notation
Matrices have a specific size and shape, just like how a toolbox has a specific size and shape. The size of a matrix is described by the number of rows and columns it has, and the shape is determined by the arrangement of the elements. Just like how a toolbox can be a different shape and size depending on the size of the tools it contains. 🤙
Officially, an n x m matrix is a matrix that consists of n rows and m columns. Each element has a unique position within the matrix, given by its row and column number. 🧱
*️⃣ Matrix Multiplication
In matrix multiplication, two matrices can be multiplied together if the number of columns in the first matrix is equal to the number of rows in the second matrix. This is known as the "matrix compatibility rule" and it is a fundamental rule that must be followed for matrix multiplication to be possible. 📏
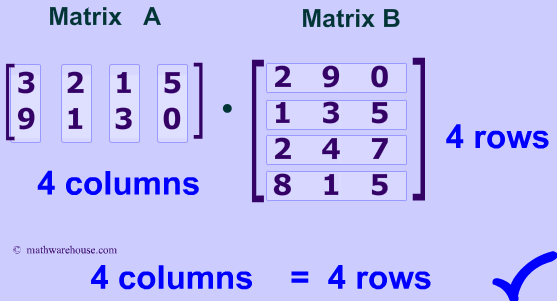
Source: Math Warehouse
For example, let A be an n x m matrix, and B be an m x p matrix. The product of these two matrices, C = A x B, is a new matrix with dimensions n x p, where the component in the ith row and jth column is calculated by taking the dot product of the ith row of the first matrix A and the jth column of the second matrix B. ✅

Source: Stack Overflow
An example of matrix multiplication operation is shown below: 👇
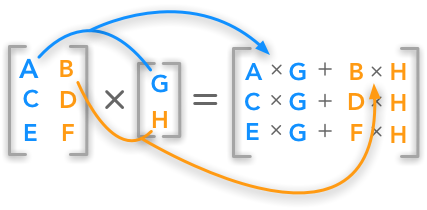
Source: Medium
🧐 What’s a Dot Product Again?
The dot product (or scalar product) is a mathematical operation used to calculate the product of two vectors. Recall from earlier sections that a vector is a mathematical object that has both a magnitude (size) and a direction. The dot product of two vectors produces a scalar value, which is a single number. 💠
To calculate the dot product of two vectors, you take the first vector, and multiply each of its components (magnitude in different directions) by the corresponding component of the second vector. Then, you add up all these products. This is similar to taking the x-coordinate of one vector, multiplying it by the x-coordinate of the other vector, taking the y-coordinate of one vector, multiplying it by the y-coordinate of the other vector and summing up the results. 👁
For example, if we have two vectors A = [3, 4] and B = [2, 1], we can calculate the dot product as: A • B = (3 * 2) + (4 * 1) = 6 + 4 = 10
<< Hide Menu
Jesse
Jesse
4.10 Matrices
A matrix is a rectangular array of numbers, symbols, or expressions that are arranged in rows ↔️ and columns. ↕️ Imagine a spreadsheet or a table with numbers arranged in rows and columns. This is similar to a matrix, but instead of being used for organizing data, matrices are used in mathematics to perform operations such as solving systems of equations, calculating determinants, and representing transformations. ⚙️
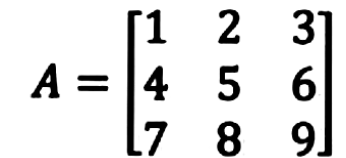
Source: StudyPug
You can also think of a matrix like a collection of different tools in a toolbox. Each tool has its own unique purpose, and you can use them to accomplish different tasks. 🔨
✍️ Notation
Matrices have a specific size and shape, just like how a toolbox has a specific size and shape. The size of a matrix is described by the number of rows and columns it has, and the shape is determined by the arrangement of the elements. Just like how a toolbox can be a different shape and size depending on the size of the tools it contains. 🤙
Officially, an n x m matrix is a matrix that consists of n rows and m columns. Each element has a unique position within the matrix, given by its row and column number. 🧱
*️⃣ Matrix Multiplication
In matrix multiplication, two matrices can be multiplied together if the number of columns in the first matrix is equal to the number of rows in the second matrix. This is known as the "matrix compatibility rule" and it is a fundamental rule that must be followed for matrix multiplication to be possible. 📏

Source: Math Warehouse
For example, let A be an n x m matrix, and B be an m x p matrix. The product of these two matrices, C = A x B, is a new matrix with dimensions n x p, where the component in the ith row and jth column is calculated by taking the dot product of the ith row of the first matrix A and the jth column of the second matrix B. ✅

Source: Stack Overflow
An example of matrix multiplication operation is shown below: 👇
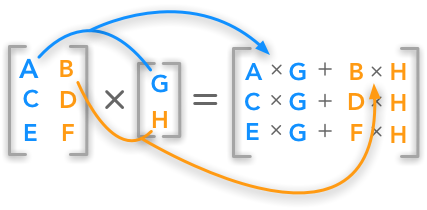
Source: Medium
🧐 What’s a Dot Product Again?
The dot product (or scalar product) is a mathematical operation used to calculate the product of two vectors. Recall from earlier sections that a vector is a mathematical object that has both a magnitude (size) and a direction. The dot product of two vectors produces a scalar value, which is a single number. 💠
To calculate the dot product of two vectors, you take the first vector, and multiply each of its components (magnitude in different directions) by the corresponding component of the second vector. Then, you add up all these products. This is similar to taking the x-coordinate of one vector, multiplying it by the x-coordinate of the other vector, taking the y-coordinate of one vector, multiplying it by the y-coordinate of the other vector and summing up the results. 👁
For example, if we have two vectors A = [3, 4] and B = [2, 1], we can calculate the dot product as: A • B = (3 * 2) + (4 * 1) = 6 + 4 = 10

© 2024 Fiveable Inc. All rights reserved.