Browse By Unit
3.12 Equivalent Representations of Trigonometric Functions
5 min read•june 18, 2024
Kashvi Panjolia
Kashvi Panjolia
Trigonometric identities are equations that are true for all values of the variables in trigonometric equations, and they can be used to simplify trigonometric expressions. In this study guide, we will be exploring these identities and learning how to use them to solve problems. By the end of this guide, you will have a solid understanding of trigonometric identities and be able to apply them to solve a wide variety of problems.
The Pythagorean Identity
The Pythagorean identity is a fundamental trigonometric identity that states that the sum of the squares of the sine and cosine of an angle is equal to one. The identity is usually written as:
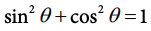
Image courtesy of CollegeBoard.
This identity can be derived from the fact that in a right triangle, the square of the length of the hypotenuse (the side opposite the right angle) is equal to the sum of the squares of the lengths of the other two sides. The trigonometric functions sine and cosine are defined based on the ratios of the sides of the right triangle, so the Pythagorean identity can be used to relate these functions to each other.
This identity can be used to prove other trigonometric identities, such as
cos^2(x) = 1 - sin^2(x)
and
sin^2(x) = 1 - cos^2(x)
It can also be used to simplify trigonometric expressions and solve trigonometric equations. Below is an example of how to simplify a trig expression using the Pythagorean identity.
Simplify the expression: 2sin^2(x) + 2cos^2(x) - 1
-
Use the Pythagorean identity (sin^2(x) + cos^2(x) = 1) to rewrite the expression as: 2(sin^2(x) + cos^2(x)) - 1
-
Substitute the Pythagorean identity into the expression to get: 2(1) - 1
-
Simplify the expression by performing the arithmetic: 2 - 1 = 1
Our final answer is 1. It's important to practice these kinds of problems so that you become comfortable using trigonometric identities to simplify expressions and solve problems. With enough practice, you'll be able to simplify even the most complex expressions quickly and easily.
More Pythagorean Identities
The Pythagorean identity can be algebraically manipulated in different ways to establish other trigonometric relationships. One example is the relationship between the tangent and secant functions, which is given by the identity:
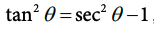
Image courtesy of CollegeBoard.
This identity can be derived by using the definitions of the tangent and secant functions, which are:
tan(x) = sin(x)/cos(x) sec(x) = 1/cos(x)
By squaring the tangent function and substituting the definition of the secant function, we get:
tan^2(x) = (sin(x)/cos(x))^2 = (sin(x))^2 / (cos(x))^2
Using the Pythagorean identity (sin^2(x) + cos^2(x) = 1), we have:
tan^2(x) = (1 - cos^2(x)) / cos^2(x) = 1/cos^2(x) - 1 = sec^2(x) - 1
Therefore, tan^2(x) = sec^2(x) - 1.
Our last Pythagorean identity is:
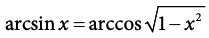
Image courtesy of CollegeBoard.
This identity can be derived by using the definitions of the sine and cosine functions, which are:
sin(x) = y and cos(x) = sqrt(1 - x^2)
If we know one of them (x) we can find the value of the expression by using arcsin or arccos, but we can also find x by using arccos(sqrt(1 - x^2)) = arcsin(x). This is the identity explained above.
It's important to note that these identities have appropriate domain restrictions. For example, the tangent and secant functions are not defined for x = 𝛑/2 + n𝛑, where n is an integer, because the denominator of the tangent function is zero in these cases. Similarly, the arcsine and arccosine functions are defined only for x in the range [-1,1].
The Sum Identities
The two sum identities for trigonometric functions, also known as the angle addition formulas, are used to find the trigonometric values of the sum of two angles in terms of the trigonometric values of the individual angles. The two sum identities are:
1. Sine Sum Identity:
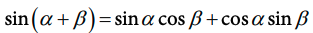
Image courtesy of CollegeBoard.
2. Cosine Sum Identity:
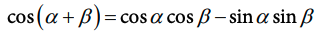
Image courtesy of CollegeBoard.
In these identities, the Greek letters alpha (α) and beta (β) represent the two angles being added together. In the following explanation, we will be using the letters a and b to represent alpha and beta, respectively.
Here's an example of using the sine sum identity to solve a problem:
Example: Find the value of sin(15 + 30)
We can use the sine sum identity to find the value of sin(15 + 30) in terms of the values of sin(15) and sin(30). The sine sum identity is:
sin(a + b) = sin(a)cos(b) + cos(a)sin(b)
We know that sin(15) = 0.2588 and sin(30) = 0.5, so we can substitute these values into the sine sum identity:
sin(15 + 30) = sin(15)cos(30) + cos(15)sin(30)
And now we can simplify the expression using the values of sin(15) and sin(30) that we know:
sin(15 + 30) = 0.2588 * 0.8660 + 0.9659 * 0.5
We can use a calculator to get the final value of the expression:
sin(15 + 30) = 0.766
So the value of sin(15 + 30) is approximately 0.766.
You can use the same approach to solve other problems using the sum identities, but make sure to use the appropriate identity for the function you are working with (sine or cosine) and to use the correct values for the angles. It's also worth mentioning that for many trigonometry problems, you have to make sure to consider the domain of the trigonometric functions, as the sum identities are only true for a specific range of angles.
The Difference and Double-Angle Identities
The difference and double-angle identities are trigonometric identities that allow you to find the values of trigonometric functions for the difference and double of an angle, respectively, in terms of the value of the function for the original angle.
- **Difference Identities:**sin(a - b) = sin(a)cos(b) - cos(a)sin(b)cos(a - b) = cos(a)cos(b) + sin(a)sin(b)
These identities can be used to simplify trigonometric expressions, solve trigonometric equations, and find the values of trigonometric functions for the difference of two angles. For example, if we know the value of sin(a) and cos(a), we can use the difference identity to find the value of sin(a - b) in terms of sin(b) and cos(b).
- **Double Angle Identities:**sin(2a) = 2sin(a)cos(a)cos(2a) = cos^2(a) - sin^2(a) = 1 - 2sin^2(a) = 2cos^2(a) - 1
These identities can be used to solve trigonometric equations involving double of an angle. For example, if we know the value of sin(a) and cos(a), we can use the double angle identity to find the value of sin(2a) or cos(2a).
Practice Problems
1. What is the value of sin(2x - 30) if sin(x) = 0.4 and cos(x) = 0.9?
a) 0.76
b) 0.24
c) -0.24
d) -0.76
Answer: c) -0.24
2. Simplify tan(2x) if sin(x) = 0.6 and cos(x) = 0.8 a) 0.75 b) 1.5 c) 2.0 d) 3.0
Answer: b) 1.5
3. Simplify cos(a + b) - cos(a - b) a) 2sin(a)sin(b) b) 2cos(a)cos(b) c) sin(a+b) - sin(a-b) d) cos(a+b) + cos(a-b)
Answer: a) 2sin(a)sin(b)
<< Hide Menu
3.12 Equivalent Representations of Trigonometric Functions
5 min read•june 18, 2024
Kashvi Panjolia
Kashvi Panjolia
Trigonometric identities are equations that are true for all values of the variables in trigonometric equations, and they can be used to simplify trigonometric expressions. In this study guide, we will be exploring these identities and learning how to use them to solve problems. By the end of this guide, you will have a solid understanding of trigonometric identities and be able to apply them to solve a wide variety of problems.
The Pythagorean Identity
The Pythagorean identity is a fundamental trigonometric identity that states that the sum of the squares of the sine and cosine of an angle is equal to one. The identity is usually written as:
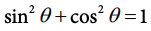
Image courtesy of CollegeBoard.
This identity can be derived from the fact that in a right triangle, the square of the length of the hypotenuse (the side opposite the right angle) is equal to the sum of the squares of the lengths of the other two sides. The trigonometric functions sine and cosine are defined based on the ratios of the sides of the right triangle, so the Pythagorean identity can be used to relate these functions to each other.
This identity can be used to prove other trigonometric identities, such as
cos^2(x) = 1 - sin^2(x)
and
sin^2(x) = 1 - cos^2(x)
It can also be used to simplify trigonometric expressions and solve trigonometric equations. Below is an example of how to simplify a trig expression using the Pythagorean identity.
Simplify the expression: 2sin^2(x) + 2cos^2(x) - 1
-
Use the Pythagorean identity (sin^2(x) + cos^2(x) = 1) to rewrite the expression as: 2(sin^2(x) + cos^2(x)) - 1
-
Substitute the Pythagorean identity into the expression to get: 2(1) - 1
-
Simplify the expression by performing the arithmetic: 2 - 1 = 1
Our final answer is 1. It's important to practice these kinds of problems so that you become comfortable using trigonometric identities to simplify expressions and solve problems. With enough practice, you'll be able to simplify even the most complex expressions quickly and easily.
More Pythagorean Identities
The Pythagorean identity can be algebraically manipulated in different ways to establish other trigonometric relationships. One example is the relationship between the tangent and secant functions, which is given by the identity:
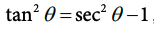
Image courtesy of CollegeBoard.
This identity can be derived by using the definitions of the tangent and secant functions, which are:
tan(x) = sin(x)/cos(x) sec(x) = 1/cos(x)
By squaring the tangent function and substituting the definition of the secant function, we get:
tan^2(x) = (sin(x)/cos(x))^2 = (sin(x))^2 / (cos(x))^2
Using the Pythagorean identity (sin^2(x) + cos^2(x) = 1), we have:
tan^2(x) = (1 - cos^2(x)) / cos^2(x) = 1/cos^2(x) - 1 = sec^2(x) - 1
Therefore, tan^2(x) = sec^2(x) - 1.
Our last Pythagorean identity is:
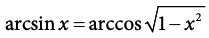
Image courtesy of CollegeBoard.
This identity can be derived by using the definitions of the sine and cosine functions, which are:
sin(x) = y and cos(x) = sqrt(1 - x^2)
If we know one of them (x) we can find the value of the expression by using arcsin or arccos, but we can also find x by using arccos(sqrt(1 - x^2)) = arcsin(x). This is the identity explained above.
It's important to note that these identities have appropriate domain restrictions. For example, the tangent and secant functions are not defined for x = 𝛑/2 + n𝛑, where n is an integer, because the denominator of the tangent function is zero in these cases. Similarly, the arcsine and arccosine functions are defined only for x in the range [-1,1].
The Sum Identities
The two sum identities for trigonometric functions, also known as the angle addition formulas, are used to find the trigonometric values of the sum of two angles in terms of the trigonometric values of the individual angles. The two sum identities are:
1. Sine Sum Identity:
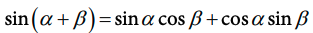
Image courtesy of CollegeBoard.
2. Cosine Sum Identity:
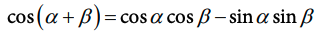
Image courtesy of CollegeBoard.
In these identities, the Greek letters alpha (α) and beta (β) represent the two angles being added together. In the following explanation, we will be using the letters a and b to represent alpha and beta, respectively.
Here's an example of using the sine sum identity to solve a problem:
Example: Find the value of sin(15 + 30)
We can use the sine sum identity to find the value of sin(15 + 30) in terms of the values of sin(15) and sin(30). The sine sum identity is:
sin(a + b) = sin(a)cos(b) + cos(a)sin(b)
We know that sin(15) = 0.2588 and sin(30) = 0.5, so we can substitute these values into the sine sum identity:
sin(15 + 30) = sin(15)cos(30) + cos(15)sin(30)
And now we can simplify the expression using the values of sin(15) and sin(30) that we know:
sin(15 + 30) = 0.2588 * 0.8660 + 0.9659 * 0.5
We can use a calculator to get the final value of the expression:
sin(15 + 30) = 0.766
So the value of sin(15 + 30) is approximately 0.766.
You can use the same approach to solve other problems using the sum identities, but make sure to use the appropriate identity for the function you are working with (sine or cosine) and to use the correct values for the angles. It's also worth mentioning that for many trigonometry problems, you have to make sure to consider the domain of the trigonometric functions, as the sum identities are only true for a specific range of angles.
The Difference and Double-Angle Identities
The difference and double-angle identities are trigonometric identities that allow you to find the values of trigonometric functions for the difference and double of an angle, respectively, in terms of the value of the function for the original angle.
- **Difference Identities:**sin(a - b) = sin(a)cos(b) - cos(a)sin(b)cos(a - b) = cos(a)cos(b) + sin(a)sin(b)
These identities can be used to simplify trigonometric expressions, solve trigonometric equations, and find the values of trigonometric functions for the difference of two angles. For example, if we know the value of sin(a) and cos(a), we can use the difference identity to find the value of sin(a - b) in terms of sin(b) and cos(b).
- **Double Angle Identities:**sin(2a) = 2sin(a)cos(a)cos(2a) = cos^2(a) - sin^2(a) = 1 - 2sin^2(a) = 2cos^2(a) - 1
These identities can be used to solve trigonometric equations involving double of an angle. For example, if we know the value of sin(a) and cos(a), we can use the double angle identity to find the value of sin(2a) or cos(2a).
Practice Problems
1. What is the value of sin(2x - 30) if sin(x) = 0.4 and cos(x) = 0.9?
a) 0.76
b) 0.24
c) -0.24
d) -0.76
Answer: c) -0.24
2. Simplify tan(2x) if sin(x) = 0.6 and cos(x) = 0.8 a) 0.75 b) 1.5 c) 2.0 d) 3.0
Answer: b) 1.5
3. Simplify cos(a + b) - cos(a - b) a) 2sin(a)sin(b) b) 2cos(a)cos(b) c) sin(a+b) - sin(a-b) d) cos(a+b) + cos(a-b)
Answer: a) 2sin(a)sin(b)

© 2024 Fiveable Inc. All rights reserved.