Browse By Unit
2.6 Competing Function Model Validation
1 min read•june 18, 2024
2.6 Competing Function Model Validation
This section’s title sounds suuuuuuuuper intimidating, but what it essentially means comes in two parts:
- We’ll learn how to construct linear, quadratic, and exponential models based on a data set provided to us; and
- We’ll learn how to validate a model constructed from a data set. In other words, is the model appropriate or not in representing the data set handed to us?
😵💫 Linear, Quadratic, or Exponential Models?
When working with data sets, it's important to be able to identify patterns and choose the appropriate function model to represent them. Two variables in a data set that demonstrate a slightly changing rate of change can be modeled by linear, exponential, and quadratic function models. Each of these models has its own characteristics and can be used to represent different types of patterns. 🪁
- Linear functions of the form f(x) = b + mx are the simplest type of function models. They are characterized by a constant rate of change, which means that the slope of the function is the same at any point. Linear functions are best suited for data sets that demonstrate a straight-line pattern, where the rate of change is constant. 🚗
- Exponential functions of the form f(x) = ab^x are characterized by a changing rate of change. The rate of change of an exponential function depends on the value of the base, which is a positive number other than 1. Exponential functions are best suited for data sets that demonstrate a growth or decay pattern, where the rate of change is not constant. ⤴️
- Quadratic functions of the form f(x) = ax^2 + bx + c, are characterized by a changing rate of change. The rate of change of a quadratic function depends on the value of the coefficient a, which can be positive or negative. Quadratic functions are best suited for data sets that demonstrate a parabolic pattern, where the rate of change is not constant. ☂️
Models can be compared based on contextual clues and applicability to determine which model is most appropriate. For example, by inspecting the data, we can check if the rate of change is constant, increasing or decreasing, or changing direction. By comparing the models to the data, we can see which one best fits the data and which one is most appropriate for making predictions.
In addition, other factors such as the simplicity of the model and the ease of interpreting the results should also be considered when choosing the most appropriate model. For example, a linear model may be simpler and easier to interpret than a quadratic model, but a quadratic model may provide a better fit to the data. 🚀
🧐 Appropriateness of Model
When fitting a model to a data set, it's important to check if the model is appropriate for the data. One way to do this is by analyzing the residuals of a regression, which are the differences between the observed values and the predicted values of the dependent variable. 💯
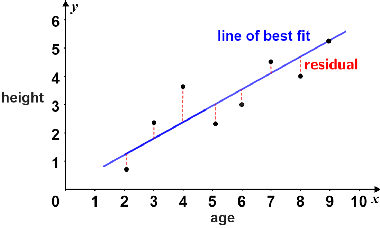
Source: Math.net
A model is considered appropriate for a data set if the graph of the residuals appears without pattern. This means that the residuals should be randomly scattered around zero and should not show any systematic pattern or trend.
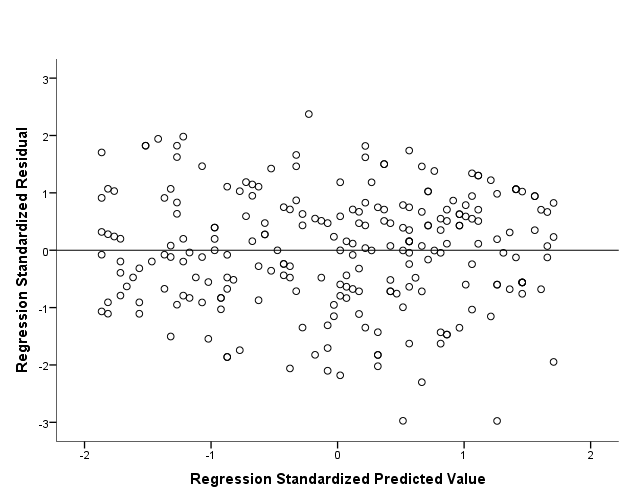
Source: ResearchGate
A scatterplot of the residuals can be used to check for patterns. If the residuals are randomly scattered around zero, it indicates that the model is fitting the data well and is appropriate for the data set. On the other hand, if the residuals show a pattern, such as a straight line, a parabola, or a sinusoidal pattern, it indicates that the model is not fitting the data well and is not appropriate for the data set.
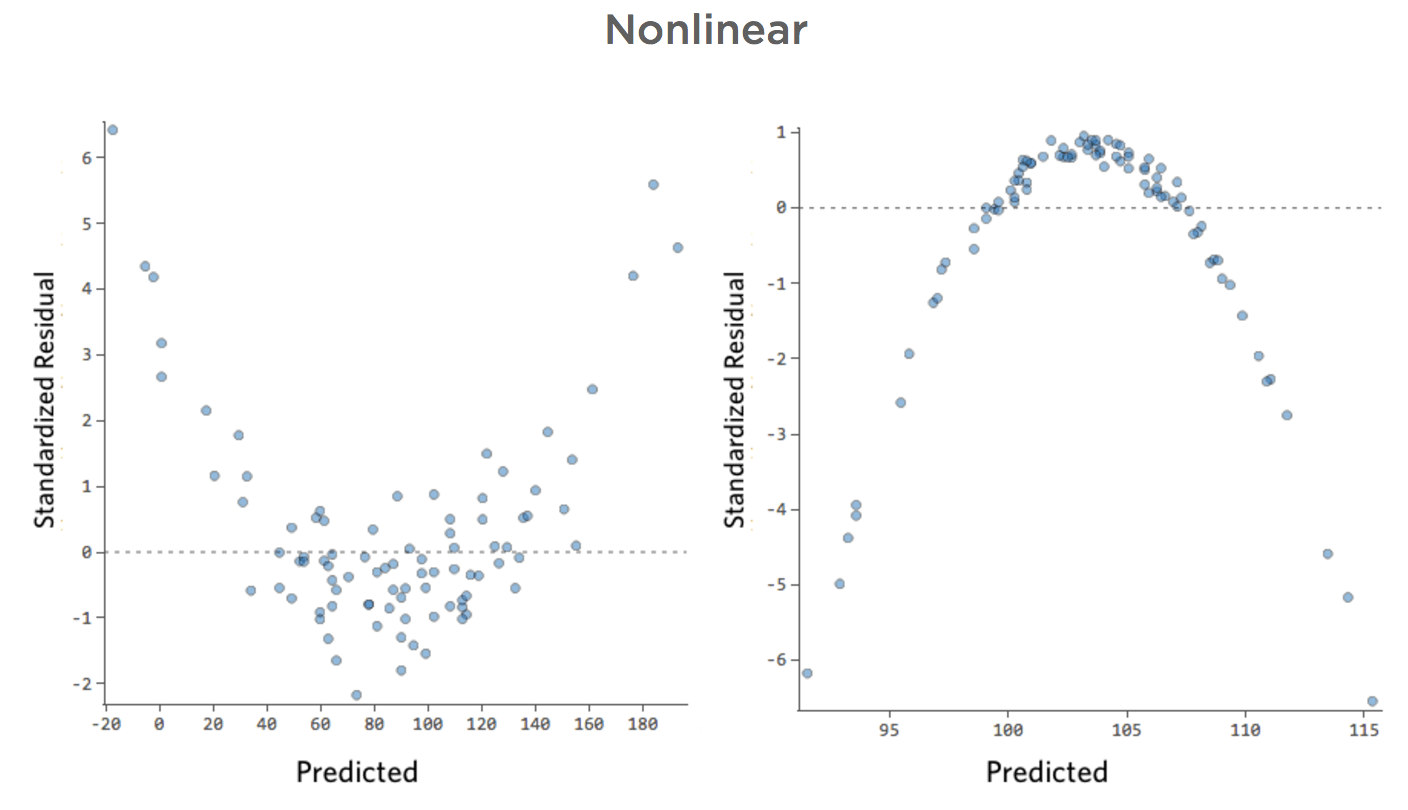
Source: Qualtrics
It's important to note that no model will fit the data perfectly, so some random scatter in the residuals is to be expected. However, if the residuals appear to show a pattern, then the model is not a good representation of the data and should be revised. 😔
😣 Errors
In addition, when fitting a model to a data set, the difference between the predicted and actual values is the error in the model. This error can be measured using various statistical measures such as mean squared error, mean absolute error, or root mean squared error. These measures give an idea of how well the model is fitting the data. 🚨

Source: Medium
Depending on the data set and context, it may be more appropriate to have an underestimate or overestimate for any given interval. 👈🏼
For example,
- In some cases, such as predicting the number of patients in a hospital, it may be more appropriate to have an overestimate, as it's better to have more resources available than not enough.
- In other cases, such as predicting the amount of money in a bank account, it may be more appropriate to have an underestimate, as it's better to have less resources available and be able to plan accordingly.
It's important to note that in some situations, it's important to minimize the error, such as in medical diagnosis, it's noteworthy to minimize the false positives and false negatives.
In other situations, it's important to maximize the accuracy, such as in self-driving cars, it's important to minimize the risk of accidents. 🎯
<< Hide Menu
2.6 Competing Function Model Validation
1 min read•june 18, 2024
2.6 Competing Function Model Validation
This section’s title sounds suuuuuuuuper intimidating, but what it essentially means comes in two parts:
- We’ll learn how to construct linear, quadratic, and exponential models based on a data set provided to us; and
- We’ll learn how to validate a model constructed from a data set. In other words, is the model appropriate or not in representing the data set handed to us?
😵💫 Linear, Quadratic, or Exponential Models?
When working with data sets, it's important to be able to identify patterns and choose the appropriate function model to represent them. Two variables in a data set that demonstrate a slightly changing rate of change can be modeled by linear, exponential, and quadratic function models. Each of these models has its own characteristics and can be used to represent different types of patterns. 🪁
- Linear functions of the form f(x) = b + mx are the simplest type of function models. They are characterized by a constant rate of change, which means that the slope of the function is the same at any point. Linear functions are best suited for data sets that demonstrate a straight-line pattern, where the rate of change is constant. 🚗
- Exponential functions of the form f(x) = ab^x are characterized by a changing rate of change. The rate of change of an exponential function depends on the value of the base, which is a positive number other than 1. Exponential functions are best suited for data sets that demonstrate a growth or decay pattern, where the rate of change is not constant. ⤴️
- Quadratic functions of the form f(x) = ax^2 + bx + c, are characterized by a changing rate of change. The rate of change of a quadratic function depends on the value of the coefficient a, which can be positive or negative. Quadratic functions are best suited for data sets that demonstrate a parabolic pattern, where the rate of change is not constant. ☂️
Models can be compared based on contextual clues and applicability to determine which model is most appropriate. For example, by inspecting the data, we can check if the rate of change is constant, increasing or decreasing, or changing direction. By comparing the models to the data, we can see which one best fits the data and which one is most appropriate for making predictions.
In addition, other factors such as the simplicity of the model and the ease of interpreting the results should also be considered when choosing the most appropriate model. For example, a linear model may be simpler and easier to interpret than a quadratic model, but a quadratic model may provide a better fit to the data. 🚀
🧐 Appropriateness of Model
When fitting a model to a data set, it's important to check if the model is appropriate for the data. One way to do this is by analyzing the residuals of a regression, which are the differences between the observed values and the predicted values of the dependent variable. 💯

Source: Math.net
A model is considered appropriate for a data set if the graph of the residuals appears without pattern. This means that the residuals should be randomly scattered around zero and should not show any systematic pattern or trend.

Source: ResearchGate
A scatterplot of the residuals can be used to check for patterns. If the residuals are randomly scattered around zero, it indicates that the model is fitting the data well and is appropriate for the data set. On the other hand, if the residuals show a pattern, such as a straight line, a parabola, or a sinusoidal pattern, it indicates that the model is not fitting the data well and is not appropriate for the data set.

Source: Qualtrics
It's important to note that no model will fit the data perfectly, so some random scatter in the residuals is to be expected. However, if the residuals appear to show a pattern, then the model is not a good representation of the data and should be revised. 😔
😣 Errors
In addition, when fitting a model to a data set, the difference between the predicted and actual values is the error in the model. This error can be measured using various statistical measures such as mean squared error, mean absolute error, or root mean squared error. These measures give an idea of how well the model is fitting the data. 🚨

Source: Medium
Depending on the data set and context, it may be more appropriate to have an underestimate or overestimate for any given interval. 👈🏼
For example,
- In some cases, such as predicting the number of patients in a hospital, it may be more appropriate to have an overestimate, as it's better to have more resources available than not enough.
- In other cases, such as predicting the amount of money in a bank account, it may be more appropriate to have an underestimate, as it's better to have less resources available and be able to plan accordingly.
It's important to note that in some situations, it's important to minimize the error, such as in medical diagnosis, it's noteworthy to minimize the false positives and false negatives.
In other situations, it's important to maximize the accuracy, such as in self-driving cars, it's important to minimize the risk of accidents. 🎯

© 2024 Fiveable Inc. All rights reserved.