Browse By Unit
1.14 Function Model Construction and Application
1 min read•june 18, 2024
1.14 Function Model Construction and Application
Continuing off our discussion about models, AP Pre-Calc expects you to not only identify which functions are most appropriate to use in modeling a specific mathematical example (or real-world application) but also construct one—whether it be linear, polynomial, piecewise, or even rational. In this section, we’ll look at various contexts and data sets to either create models or interpret conclusions! 👷
📊 Linear, Polynomial, and Piecewise-Defined Function Models
A model can be constructed based on restrictions identified in a mathematical or contextual scenario. These restrictions can include domain and range restrictions, as well as any underlying assumptions about the system being modeled. These restrictions can help to ensure that the model is a valid representation of the real-world system, and that the predictions and conclusions that are made from the model are valid and relevant. 🙅
In the example below, the function model is defined such that x is either less than or equal to -3 or greater than 3.
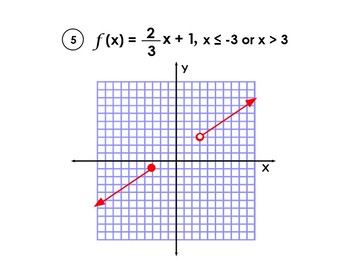
Source: TPT
A model of a data set or a contextual scenario can also be constructed using transformations of the parent function. A parent function is a basic function that can be transformed in various ways (such as shifting, reflecting, stretching) to create other functions that have similar properties but different characteristics. This method can be used to construct a model that is a good fit for the data set or contextual scenario being modeled. 🙌
In the example below, a complicated model may look like the one in green, so a mathematician might start with a simple (black) function before adding elements like constant multiples and shifts (as seen in the blue and orange transformations) before eventually arrive to a function model relatively similar to the green one.
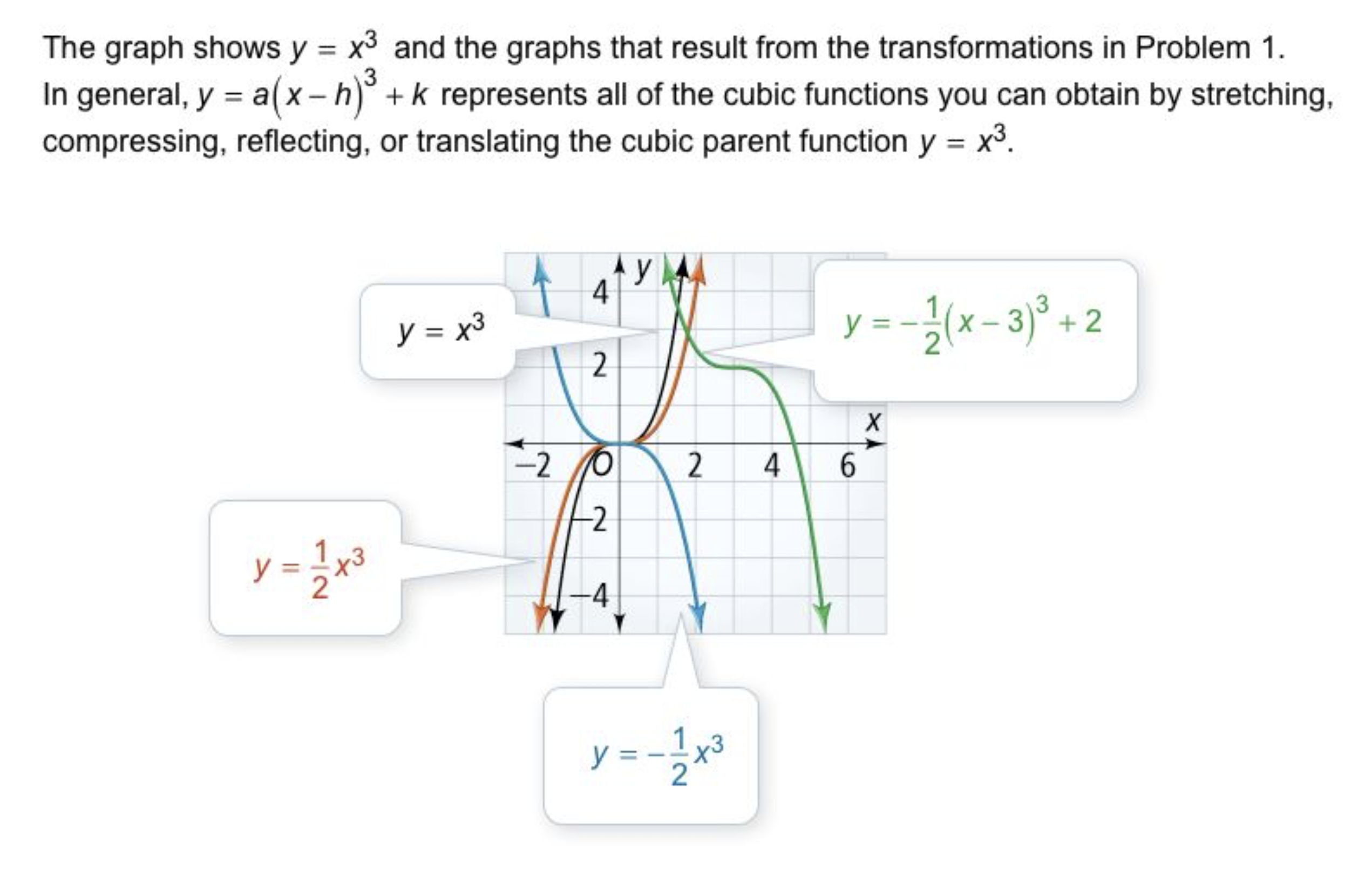
Source: Formative
A model of a data set can also be constructed using technology and regressions. Regression is a statistical method used to analyze the relationship between variables, and can be used to construct a model of a data set. This method can be useful when the data set is too large or complex to be modeled by hand, or when the underlying relationship between the variables is not immediately clear. 📱

Source: Harvard Business Review (described in image as HBR.org)
A piecewise-defined function model can be constructed through a combination of modeling techniques. For example, a piecewise-defined function can be constructed by combining multiple polynomial functions or other functions defined over non-overlapping domain intervals. This can be useful for modeling systems that have different behaviors over different intervals, and can help to create a more accurate and detailed model of the system being modeled. 🤓
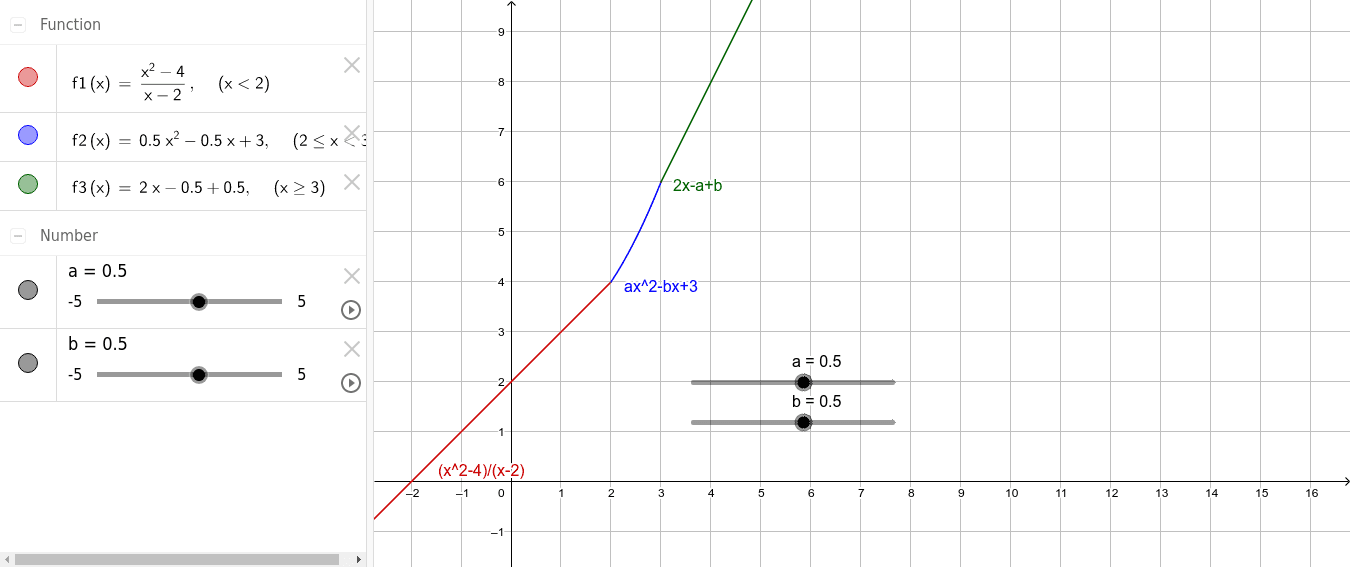
Source: GeoGebra
Remember that the choice of model construction technique will depend on the specific characteristics of the data set or contextual scenario being modeled and the goals of the analysis. Therefore, it’s important to consider multiple modeling techniques and to evaluate the suitability of each one for the problem at hand rather than blindly jumping into an easier modeling technique out of convenience! 💡 Rational Functions****
Data sets and aspects of contextual scenarios involving quantities that are inversely proportional can often be modeled by rational functions. Recall that a rational function is a function that can be written in the form , where p(x) and q(x) are polynomial functions. 🧑💻
As introduced above, rational functions are useful for modeling systems where the quantities being considered are inversely proportional. For example, the magnitudes of both gravitational force and electromagnetic force between objects are inversely proportional to the objects’ squared distance. 🛣️
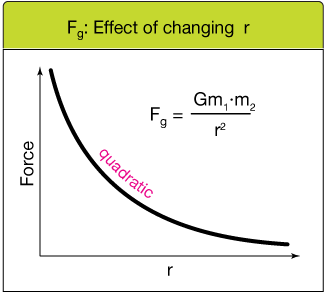
For example, the gravitational force between two objects is given by the formula , where F is the gravitational force, G is the gravitational constant, m1 and m2 are the masses of the objects, and r is the distance between the objects. This equation can be rewritten as , which is a rational function. 🚀

Source: Hyperphysics
Another example is the electromagnetic force between two charges is given by Coulomb's law, which states that the force is inversely proportional to the square of the distance between the charges. This can be represented by , where F is the force, k is a constant, q1 and q2 are the charges, and r is the distance between the charges. 🧲

Source: Hyperphysics
In both examples, the force is inversely proportional to the square of the distance between the objects, and can be modeled by rational functions. Beyond these, there are many other physical laws and phenomena that can be modeled using rational functions! 🤯
Source: Xatly
🖌️ Drawing Conclusions and Adding Units
A model can be used to draw conclusions about the modeled data set or contextual scenario. Once a model is constructed, it can be used to answer key questions about the data set or contextual scenario, such as how the variables are related, what patterns exist in the data, and what predictions can be made about future values or behavior.
One of the key uses of a model is to predict values of the modeled variable based on the values of the independent variable. For example, if a model is constructed to predict the price of a product based on the number of units sold, the model can be used to predict… the price of a product if a certain number of units are sold! Surprisingly straightforward, huh? 😉
Additionally, a model can be used to predict rates of change, average rates of change, and changing rates of change in the modeled data set or contextual scenario. For example, a model can be used to predict how the price of a product changes as the number of units sold increases, or to predict the average rate of change of the price as the number of units sold changes. 💰
It's important to note that when interpreting the results of a model, it's necessary to pay attention to the units of measure of the modeled variables, and to extract or infer the appropriate units of measure from the given context. For example, in the previous example, if the model is predicting price in dollars, it's important to interpret the results in dollars, and not in any other currency.
<< Hide Menu
1.14 Function Model Construction and Application
1 min read•june 18, 2024
1.14 Function Model Construction and Application
Continuing off our discussion about models, AP Pre-Calc expects you to not only identify which functions are most appropriate to use in modeling a specific mathematical example (or real-world application) but also construct one—whether it be linear, polynomial, piecewise, or even rational. In this section, we’ll look at various contexts and data sets to either create models or interpret conclusions! 👷
📊 Linear, Polynomial, and Piecewise-Defined Function Models
A model can be constructed based on restrictions identified in a mathematical or contextual scenario. These restrictions can include domain and range restrictions, as well as any underlying assumptions about the system being modeled. These restrictions can help to ensure that the model is a valid representation of the real-world system, and that the predictions and conclusions that are made from the model are valid and relevant. 🙅
In the example below, the function model is defined such that x is either less than or equal to -3 or greater than 3.

Source: TPT
A model of a data set or a contextual scenario can also be constructed using transformations of the parent function. A parent function is a basic function that can be transformed in various ways (such as shifting, reflecting, stretching) to create other functions that have similar properties but different characteristics. This method can be used to construct a model that is a good fit for the data set or contextual scenario being modeled. 🙌
In the example below, a complicated model may look like the one in green, so a mathematician might start with a simple (black) function before adding elements like constant multiples and shifts (as seen in the blue and orange transformations) before eventually arrive to a function model relatively similar to the green one.

Source: Formative
A model of a data set can also be constructed using technology and regressions. Regression is a statistical method used to analyze the relationship between variables, and can be used to construct a model of a data set. This method can be useful when the data set is too large or complex to be modeled by hand, or when the underlying relationship between the variables is not immediately clear. 📱

Source: Harvard Business Review (described in image as HBR.org)
A piecewise-defined function model can be constructed through a combination of modeling techniques. For example, a piecewise-defined function can be constructed by combining multiple polynomial functions or other functions defined over non-overlapping domain intervals. This can be useful for modeling systems that have different behaviors over different intervals, and can help to create a more accurate and detailed model of the system being modeled. 🤓

Source: GeoGebra
Remember that the choice of model construction technique will depend on the specific characteristics of the data set or contextual scenario being modeled and the goals of the analysis. Therefore, it’s important to consider multiple modeling techniques and to evaluate the suitability of each one for the problem at hand rather than blindly jumping into an easier modeling technique out of convenience! 💡 Rational Functions****
Data sets and aspects of contextual scenarios involving quantities that are inversely proportional can often be modeled by rational functions. Recall that a rational function is a function that can be written in the form , where p(x) and q(x) are polynomial functions. 🧑💻
As introduced above, rational functions are useful for modeling systems where the quantities being considered are inversely proportional. For example, the magnitudes of both gravitational force and electromagnetic force between objects are inversely proportional to the objects’ squared distance. 🛣️
For example, the gravitational force between two objects is given by the formula , where F is the gravitational force, G is the gravitational constant, m1 and m2 are the masses of the objects, and r is the distance between the objects. This equation can be rewritten as , which is a rational function. 🚀

Source: Hyperphysics
Another example is the electromagnetic force between two charges is given by Coulomb's law, which states that the force is inversely proportional to the square of the distance between the charges. This can be represented by , where F is the force, k is a constant, q1 and q2 are the charges, and r is the distance between the charges. 🧲

Source: Hyperphysics
In both examples, the force is inversely proportional to the square of the distance between the objects, and can be modeled by rational functions. Beyond these, there are many other physical laws and phenomena that can be modeled using rational functions! 🤯

Source: Xatly
🖌️ Drawing Conclusions and Adding Units
A model can be used to draw conclusions about the modeled data set or contextual scenario. Once a model is constructed, it can be used to answer key questions about the data set or contextual scenario, such as how the variables are related, what patterns exist in the data, and what predictions can be made about future values or behavior.
One of the key uses of a model is to predict values of the modeled variable based on the values of the independent variable. For example, if a model is constructed to predict the price of a product based on the number of units sold, the model can be used to predict… the price of a product if a certain number of units are sold! Surprisingly straightforward, huh? 😉
Additionally, a model can be used to predict rates of change, average rates of change, and changing rates of change in the modeled data set or contextual scenario. For example, a model can be used to predict how the price of a product changes as the number of units sold increases, or to predict the average rate of change of the price as the number of units sold changes. 💰
It's important to note that when interpreting the results of a model, it's necessary to pay attention to the units of measure of the modeled variables, and to extract or infer the appropriate units of measure from the given context. For example, in the previous example, if the model is predicting price in dollars, it's important to interpret the results in dollars, and not in any other currency.

© 2024 Fiveable Inc. All rights reserved.