Browse By Unit
Josh Argo
Jed Quiaoit
Josh Argo
Jed Quiaoit
Tests from Two-Way Tables
Another form of data that we can use χ2 tests for involves data from a two-way table (like the one pictured below). 🎨
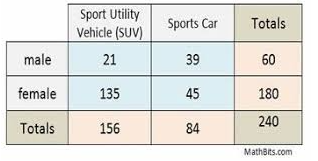
Image Taken from MathBitsNotebook
When performing a χ2 test from a two way table, there are two different tests we may have to perform and choosing which one can be tricky.
Test for Homogeneity
A chi-squared test for homogeneity is used to compare the distribution of a categorical variable between two or more independent groups or populations. It is used to test the null hypothesis that the proportions of the categories are the same in all the groups. In other words, we'll have to use the chi-squared test for homogeneity when we're comparing two different populations and if two different populations have different amounts for a given categorical variable. 🍞
Test for Independence
A chi-squared test for independence is used to examine the relationship between two categorical variables in a single population. It is used to test the null hypothesis that the two variables are independent, meaning that the presence or absence of one variable does not affect the probability of the other variable. In other words, we'll use this test when we're comparing within one population to see if two categorical variables are associated within the one population, we would use a χ2 test for independence. 💥
Expected Counts
Regardless of which test we are doing, we will be comparing two multi-row/column matrices rather than just two rows or columns. This means we have to calculate the expected counts matrix based off of our observed counts table. This will be done by doing the following for each cell: 😀

where n = table total.
Example
In the first cell on the two way table above on SUV and sports car ownership in regard to male or female, we would take the total male (60) and the total SUV (156), multiply those to get 9360. Then we would divide that total by our table total (240) and get 39. We would complete this process for all steps to create our expected count table. 🚗
Our final expected counts answer would be:
| | SUV | Sports Car | | --- | --- | --- | | Male | 39 | 21 | | Female | 117 | 63 |
Applications
In the next sections, we will talk about setting up the two types of χ2 tests regarding a two way table and how we will use these observed and expected counts to determine if we have association or homogeneity between our two variables/populations. Stay tuned 'til then! 😉
🎥 Watch: AP Stats Unit 8 - Chi Squared Tests
<< Hide Menu
Josh Argo
Jed Quiaoit
Josh Argo
Jed Quiaoit
Tests from Two-Way Tables
Another form of data that we can use χ2 tests for involves data from a two-way table (like the one pictured below). 🎨

Image Taken from MathBitsNotebook
When performing a χ2 test from a two way table, there are two different tests we may have to perform and choosing which one can be tricky.
Test for Homogeneity
A chi-squared test for homogeneity is used to compare the distribution of a categorical variable between two or more independent groups or populations. It is used to test the null hypothesis that the proportions of the categories are the same in all the groups. In other words, we'll have to use the chi-squared test for homogeneity when we're comparing two different populations and if two different populations have different amounts for a given categorical variable. 🍞
Test for Independence
A chi-squared test for independence is used to examine the relationship between two categorical variables in a single population. It is used to test the null hypothesis that the two variables are independent, meaning that the presence or absence of one variable does not affect the probability of the other variable. In other words, we'll use this test when we're comparing within one population to see if two categorical variables are associated within the one population, we would use a χ2 test for independence. 💥
Expected Counts
Regardless of which test we are doing, we will be comparing two multi-row/column matrices rather than just two rows or columns. This means we have to calculate the expected counts matrix based off of our observed counts table. This will be done by doing the following for each cell: 😀

where n = table total.
Example
In the first cell on the two way table above on SUV and sports car ownership in regard to male or female, we would take the total male (60) and the total SUV (156), multiply those to get 9360. Then we would divide that total by our table total (240) and get 39. We would complete this process for all steps to create our expected count table. 🚗
Our final expected counts answer would be:
| | SUV | Sports Car | | --- | --- | --- | | Male | 39 | 21 | | Female | 117 | 63 |
Applications
In the next sections, we will talk about setting up the two types of χ2 tests regarding a two way table and how we will use these observed and expected counts to determine if we have association or homogeneity between our two variables/populations. Stay tuned 'til then! 😉
🎥 Watch: AP Stats Unit 8 - Chi Squared Tests

© 2024 Fiveable Inc. All rights reserved.