Browse By Unit
4.11 Parameters for a Binomial Distribution
3 min read•june 18, 2024
Kanya Shah
Jed Quiaoit
Kanya Shah
Jed Quiaoit
In order to use the binomial distribution to model a random event, the event must meet the following four conditions: 4️⃣
- Binary: The possible outcomes of each trial can be classified as a success or a failure.
- Independent: Trials must be independent. That is, knowing the outcome of one trial must not tell us anything about the outcome of any other trial.
- Fixed number of trials: The number of trials n of the chance process must be fixed in advance.
- Same probability of success: There must be the same probability of success p on each trial. (A mnemonic device that might help is BINS: binary, independent, number, same probability!)
If any of these conditions is not met, then the event cannot be modeled using the binomial distribution. For example, suppose you want to use the binomial distribution to model the number of heads in 10 flips of a biased coin that has a probability of heads of 0.8 on the first flip, 0.6 on the second flip, and so on. In this case, the probability of success is not the same on each trial, so the event cannot be modeled using the binomial distribution.
Describing Mean and Standard Deviation of Binomial Variables
Before proceeding, it's important to note that these formulae only apply in binomial settings, where the conditions for the binomial distribution are met. If the conditions for the binomial distribution are not met, then these formulae will not be appropriate for calculating the mean and standard deviation of the random variable. ✔️
- Mean -- The mean (expected value) of a binomial random variable X, which represents the number of successes in n independent trials with probability of success p, is given by: mean = E(X) = n * p
- Standard deviation -- The standard deviation of a binomial random variable X, which represents the number of successes in n independent trials with probability of success p, is given by: standard deviation = σx = sqrt(n * p * (1-p))
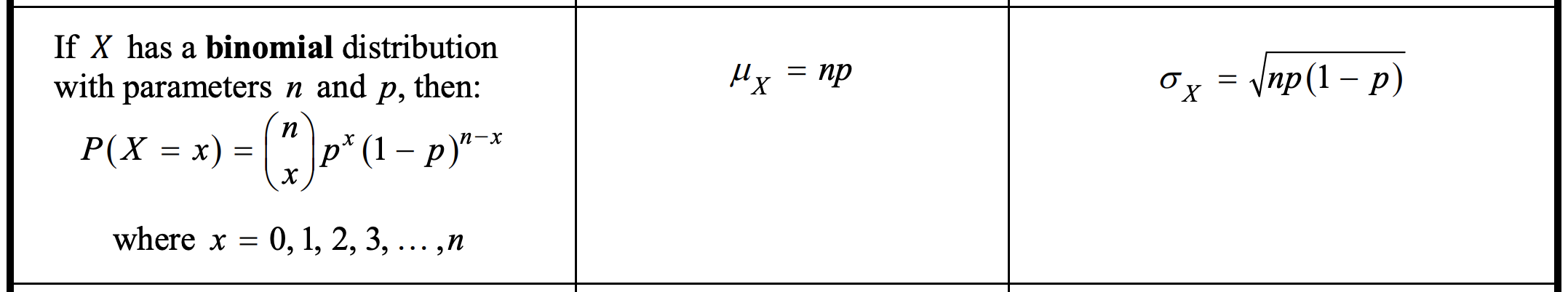
Source: College Board (AP Statistics Formula Sheet and Tables)
Binomial Distributions in Statistical Sampling
Another common rule of thumb used to determine whether a binomial model is appropriate for a random event is the 10% condition, which states that if you are taking a random sample of size n from a population of size N, and n is less than 10% of N (that is, n < 0.10N), then you can use a binomial model to describe the number of successes in the sample. 🛞
This rule is based on the assumption that the sample is representative of the population, and that the probability of success is the same in the sample as it is in the population. If these assumptions are not met, then the binomial model may not be appropriate, even if the sample size is less than 10% of the population size.
🎥 Watch: AP Stats - Probability: Random Variables, Binomial/Geometric Distributions
<< Hide Menu
4.11 Parameters for a Binomial Distribution
3 min read•june 18, 2024
Kanya Shah
Jed Quiaoit
Kanya Shah
Jed Quiaoit
In order to use the binomial distribution to model a random event, the event must meet the following four conditions: 4️⃣
- Binary: The possible outcomes of each trial can be classified as a success or a failure.
- Independent: Trials must be independent. That is, knowing the outcome of one trial must not tell us anything about the outcome of any other trial.
- Fixed number of trials: The number of trials n of the chance process must be fixed in advance.
- Same probability of success: There must be the same probability of success p on each trial. (A mnemonic device that might help is BINS: binary, independent, number, same probability!)
If any of these conditions is not met, then the event cannot be modeled using the binomial distribution. For example, suppose you want to use the binomial distribution to model the number of heads in 10 flips of a biased coin that has a probability of heads of 0.8 on the first flip, 0.6 on the second flip, and so on. In this case, the probability of success is not the same on each trial, so the event cannot be modeled using the binomial distribution.
Describing Mean and Standard Deviation of Binomial Variables
Before proceeding, it's important to note that these formulae only apply in binomial settings, where the conditions for the binomial distribution are met. If the conditions for the binomial distribution are not met, then these formulae will not be appropriate for calculating the mean and standard deviation of the random variable. ✔️
- Mean -- The mean (expected value) of a binomial random variable X, which represents the number of successes in n independent trials with probability of success p, is given by: mean = E(X) = n * p
- Standard deviation -- The standard deviation of a binomial random variable X, which represents the number of successes in n independent trials with probability of success p, is given by: standard deviation = σx = sqrt(n * p * (1-p))
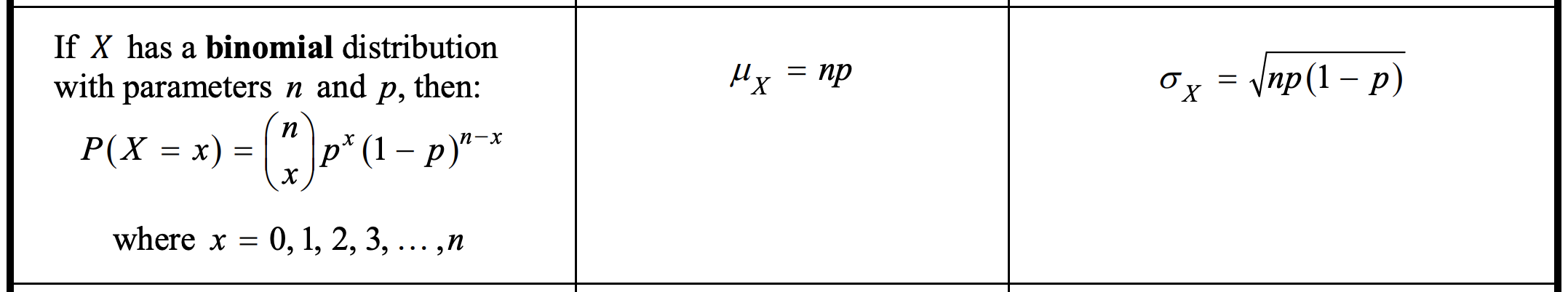
Source: College Board (AP Statistics Formula Sheet and Tables)
Binomial Distributions in Statistical Sampling
Another common rule of thumb used to determine whether a binomial model is appropriate for a random event is the 10% condition, which states that if you are taking a random sample of size n from a population of size N, and n is less than 10% of N (that is, n < 0.10N), then you can use a binomial model to describe the number of successes in the sample. 🛞
This rule is based on the assumption that the sample is representative of the population, and that the probability of success is the same in the sample as it is in the population. If these assumptions are not met, then the binomial model may not be appropriate, even if the sample size is less than 10% of the population size.
🎥 Watch: AP Stats - Probability: Random Variables, Binomial/Geometric Distributions

© 2024 Fiveable Inc. All rights reserved.