Browse By Unit
Peter Apps
Peter Apps
What's a Capacitor?
A capacitor is a device that can be used to store charge, and therefore, electrical potential energy. They are used in a wide range of electrical devices including the flash on your cell phone camera. There are several different ways to construct a capacitor, but we're going to focus on the parallel-plate version.

Image from Wikipedia
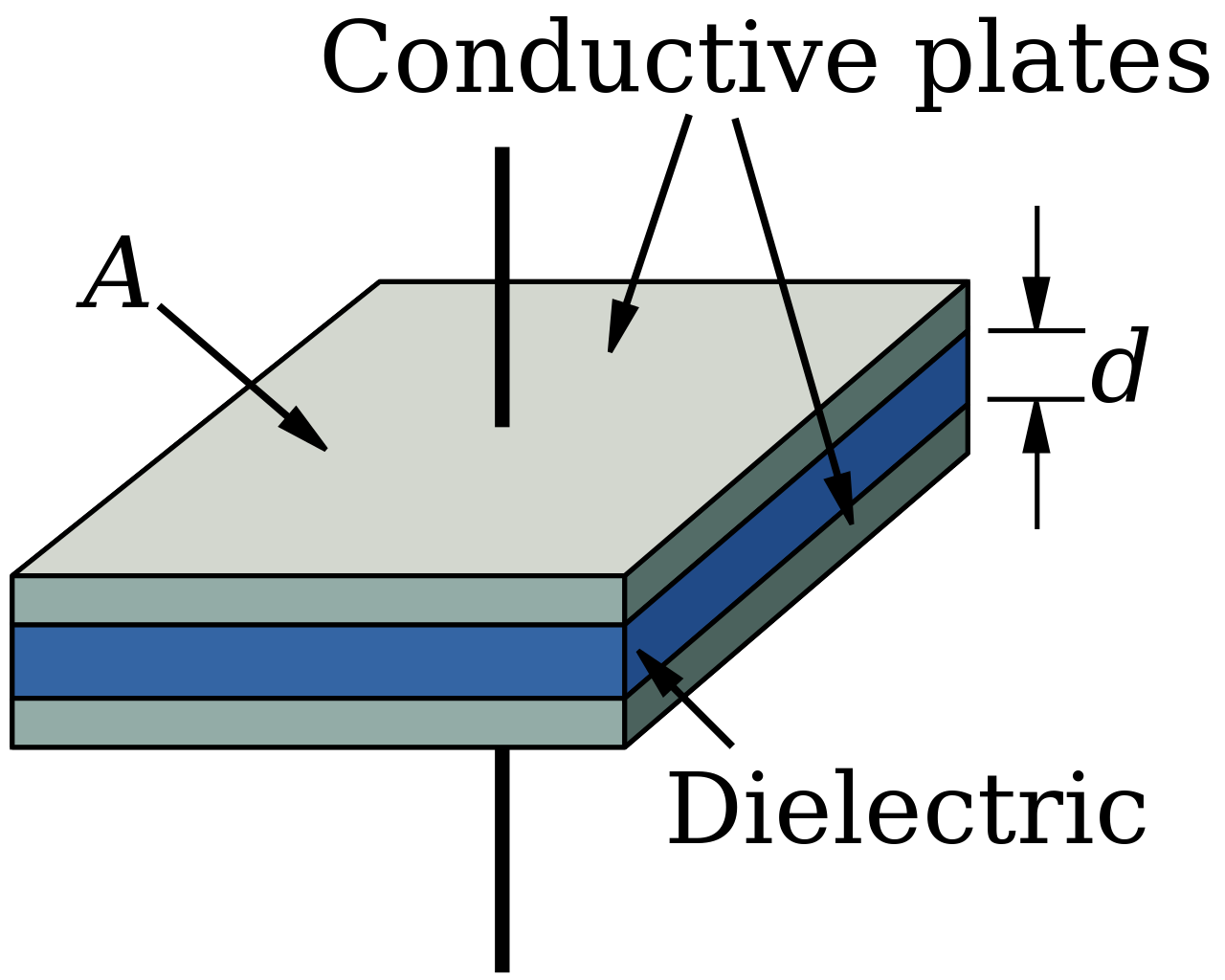
Image from Wikipedia
The parallel plate capacitor is created by taking two conductive plates and separating them by a small distance. A dielectric is often added to increase the amount of charge a capacitor can store. We'll discuss more about dielectrics in the next section.
Theory Time - Parallel Plate Capacitor 🎓
Let's create a simple capacitor using two metal plates and connect them to a battery to charge them up. Recall from Unit 1, that the strength of the electric field is proportional to the amount charge.
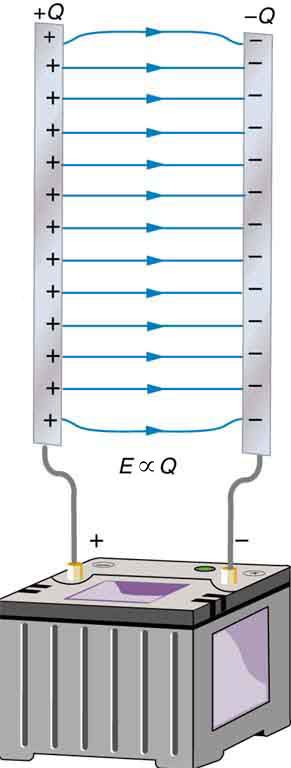
Image from opentextbc.ca
We also know that the potential difference (V) between the plates is related to the electric field through ∆V = -∫E*dr. Following this thought process, we can see that V is proportional to Q as well. The more charge that gets stored on each plate, the stronger the field, and the higher the voltage between the plates will be. We'll define a new quantity, capacitance (C), as the constant of proportionality between V and Q such that:
The unit for capacitance is the Farad (F), where 1F = 1C / 1V.
We can also define capacitance in terms of the physical dimensions of the capacitor. Recall that σ = Q/A (area charge density for a sheet of charge, and E = σ / e0 for a conductive plate.
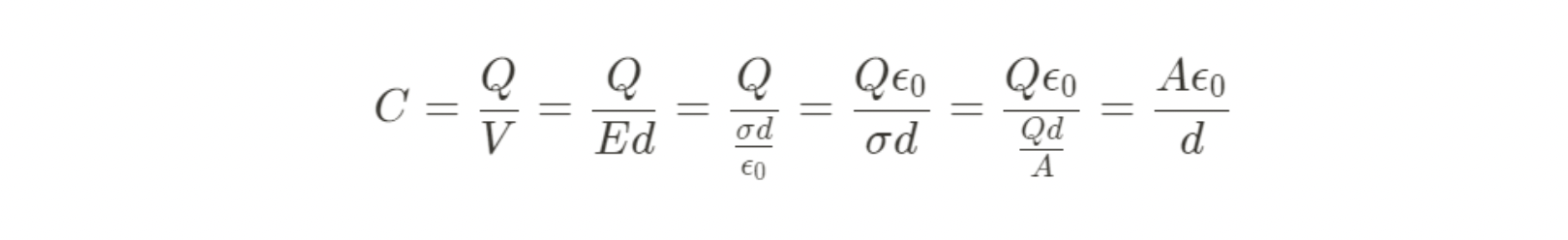
** This equation is for a capacitor where the plates are separated by air. We're going to tweak this equation a bit in the dielectric section when we discuss different materials to place between the plates.**
From here, we can see that capacitance is directly proportional to the area of the plates (A) and inversely proportional to the distance between them. This should make sense since a larger plate has more room for the charge to occupy and, therefore, moe should be able to fit on it.
Other Types of Capacitors
You might also be asked to derive capacitance equations for other geometrically shaped capacitors on the AP exam (even though the most common are parallel plate and spherical). The basic process is the same for each of these. We'll need to use the appropriate electric field equation (from Unit 1) and use it to find the change in voltage (∆V = ∫E*dr) from which we can find the capacitance equation C = Q/V. You may also need to use ρ, σ, λ for volume, area, and linear charge densities respectively.
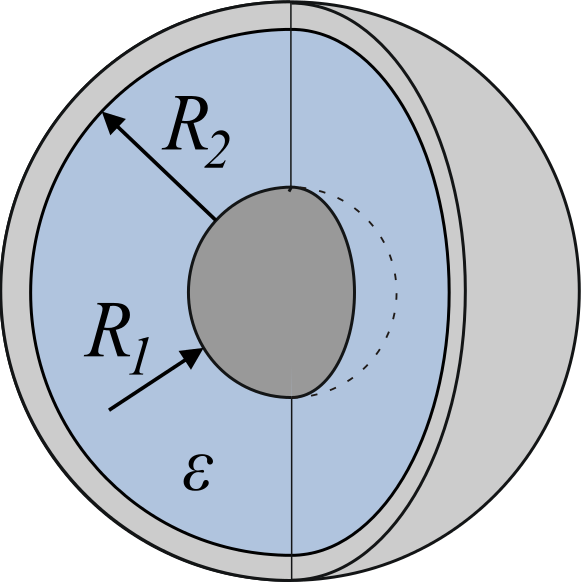
Image from Wikipedia.org
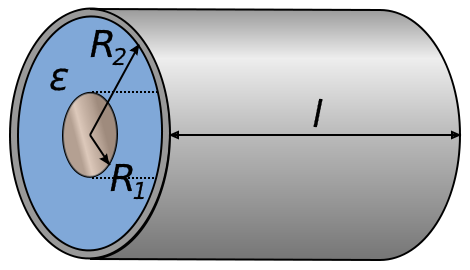
Image from toppr.com
Energy in a Capacitor 💡
Because the capacitor stores charge, it also stores electric potential energy (Uc). The amount of energy stored can be determined through the following derivation. We're going to imagine moving a tiny bit of charge (dq) from one side of the capacitor to the other. The charge will gain energy that's proportional to the potential difference passed through.
Take a few minutes and check out this Phet Simulation where you can alter the physical properties of a parallel plate capacitor and see the effect on voltage, field strength and energy stored
Practice Questions 👍
- A 20 µF parallel-plate capacitor is fully charged to 20 V. The energy stored in the capacitor is most nearly __________.- Answer:
- A capacitor with circular parallel plates of radius R that are separated by a distance d has a capacitance of C. What would the capacitance (in terms of C ) be if the plates had radius 2R and were separated by a distance d/2?- Answer:
Practice FRQ
An isolated conducting sphere of radius a = 0.20 m is at a potential of -2,000 V.
(a) Determine the charge Q_0 on the sphere.
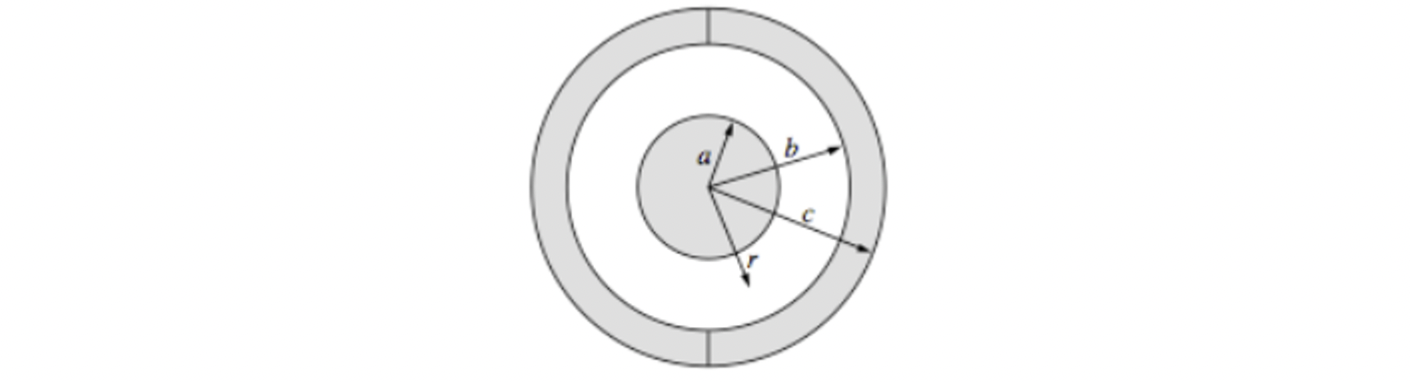
The charge sphere is then concentrically surrounded by two uncharged conducting hemispheres of inner radius b = 0.40 m and outer radius c = 0.50 m, which are joined together as shown above, forming a spherical capacitor. A wire is connected from the outer sphere to ground, and then removed.
(b) Determine the magnitude of the electric field in the following regions as a function of the distance r from the center of the inner sphere.
i. r < a
ii. a < r < b
iii. b < r < c
iv. r > c
(c) Determine the magnitude of the potential difference between the sphere and the conducting shell.
(d) Determine the capacitance of the spherical capacitor.
Answer:
<< Hide Menu
Peter Apps
Peter Apps
What's a Capacitor?
A capacitor is a device that can be used to store charge, and therefore, electrical potential energy. They are used in a wide range of electrical devices including the flash on your cell phone camera. There are several different ways to construct a capacitor, but we're going to focus on the parallel-plate version.

Image from Wikipedia

Image from Wikipedia
The parallel plate capacitor is created by taking two conductive plates and separating them by a small distance. A dielectric is often added to increase the amount of charge a capacitor can store. We'll discuss more about dielectrics in the next section.
Theory Time - Parallel Plate Capacitor 🎓
Let's create a simple capacitor using two metal plates and connect them to a battery to charge them up. Recall from Unit 1, that the strength of the electric field is proportional to the amount charge.

Image from opentextbc.ca
We also know that the potential difference (V) between the plates is related to the electric field through ∆V = -∫E*dr. Following this thought process, we can see that V is proportional to Q as well. The more charge that gets stored on each plate, the stronger the field, and the higher the voltage between the plates will be. We'll define a new quantity, capacitance (C), as the constant of proportionality between V and Q such that:
The unit for capacitance is the Farad (F), where 1F = 1C / 1V.
We can also define capacitance in terms of the physical dimensions of the capacitor. Recall that σ = Q/A (area charge density for a sheet of charge, and E = σ / e0 for a conductive plate.
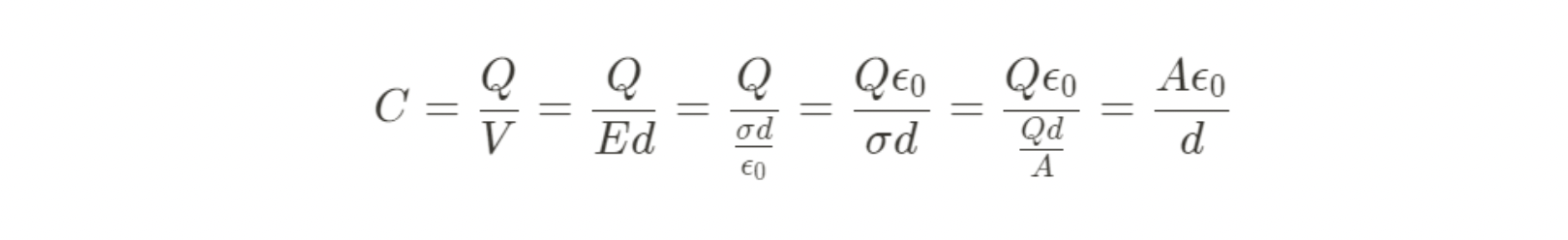
** This equation is for a capacitor where the plates are separated by air. We're going to tweak this equation a bit in the dielectric section when we discuss different materials to place between the plates.**
From here, we can see that capacitance is directly proportional to the area of the plates (A) and inversely proportional to the distance between them. This should make sense since a larger plate has more room for the charge to occupy and, therefore, moe should be able to fit on it.
Other Types of Capacitors
You might also be asked to derive capacitance equations for other geometrically shaped capacitors on the AP exam (even though the most common are parallel plate and spherical). The basic process is the same for each of these. We'll need to use the appropriate electric field equation (from Unit 1) and use it to find the change in voltage (∆V = ∫E*dr) from which we can find the capacitance equation C = Q/V. You may also need to use ρ, σ, λ for volume, area, and linear charge densities respectively.

Image from Wikipedia.org

Image from toppr.com
Energy in a Capacitor 💡
Because the capacitor stores charge, it also stores electric potential energy (Uc). The amount of energy stored can be determined through the following derivation. We're going to imagine moving a tiny bit of charge (dq) from one side of the capacitor to the other. The charge will gain energy that's proportional to the potential difference passed through.
Take a few minutes and check out this Phet Simulation where you can alter the physical properties of a parallel plate capacitor and see the effect on voltage, field strength and energy stored
Practice Questions 👍
- A 20 µF parallel-plate capacitor is fully charged to 20 V. The energy stored in the capacitor is most nearly __________.- Answer:
- A capacitor with circular parallel plates of radius R that are separated by a distance d has a capacitance of C. What would the capacitance (in terms of C ) be if the plates had radius 2R and were separated by a distance d/2?- Answer:
Practice FRQ
An isolated conducting sphere of radius a = 0.20 m is at a potential of -2,000 V.
(a) Determine the charge Q_0 on the sphere.

The charge sphere is then concentrically surrounded by two uncharged conducting hemispheres of inner radius b = 0.40 m and outer radius c = 0.50 m, which are joined together as shown above, forming a spherical capacitor. A wire is connected from the outer sphere to ground, and then removed.
(b) Determine the magnitude of the electric field in the following regions as a function of the distance r from the center of the inner sphere.
i. r < a
ii. a < r < b
iii. b < r < c
iv. r > c
(c) Determine the magnitude of the potential difference between the sphere and the conducting shell.
(d) Determine the capacitance of the spherical capacitor.
Answer:

© 2024 Fiveable Inc. All rights reserved.