Browse By Unit
1.5 Other Charge Distributions - Fields & Potentials
4 min read•june 18, 2024
Peter Apps
Peter Apps
This topic is a catch-all for more advanced applications of Charge Distributions, Gauss' Law, and calculating Electric Potentials. All of the concepts are covered in the previous sections, so if you need to, re-read those first.
Extended Charge Distributions
Up until now, we've dealt with charged objects as points, but sometimes we can't approximate the charge to be in a single location. These extended charge distributions are cases where the charge is in a ring, or line, or sheet.
The proccess for tackling all of these are very similar. We're going to chunk the total charge Q into into pieces, dq, which each contributes a partial field, dE. The entire equation is dE = k dq/r^2 * r, where r is the radius vector. By integrating that equation, we can sum up all of the dq which sums all of the dE to find the total field E.
Ring of Charge Example:
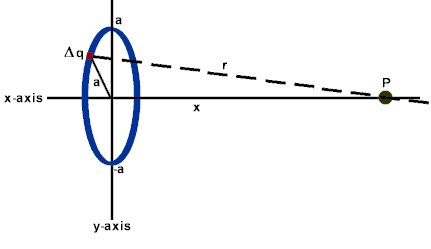
Image from dev.physicslab.org
If we assume that x >>> a, then we get the same result as for a point charge we found in Section 1. 2! This is a more general case, but we can see that it simplifies to the basic case!
Line of Charge Example:
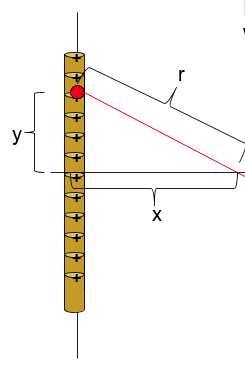
Image created by author
Start by finding dq in terms of y using linear charge density ƛ.

Then, plug into our integral just like in the previous example. In this case, we can find r by using the pythagoreon theorem between y and x.
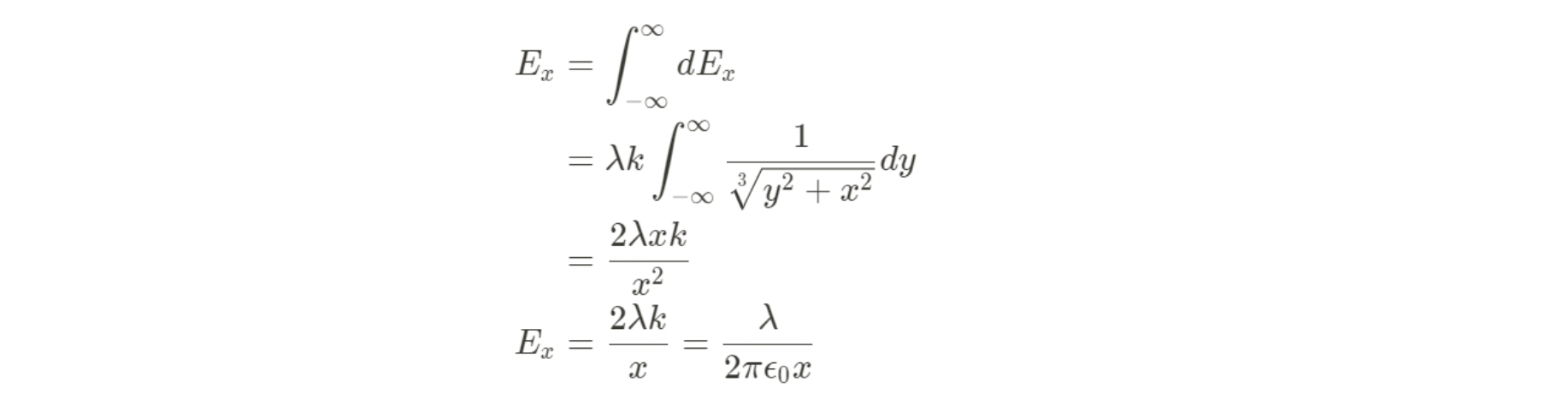
Gauss' Law for Various Shapes
You should be able to use Gauss' Law to derive these if you need to. Check out hyperphysics for more info.
Line of Charge:
Imagine enclosing the line of charge in a cylinder, use linear charge density λ = Q/L to find the enclosed charge, and then use A=2πrL.
Point, Hoop, or Sphere (fully enclosed):
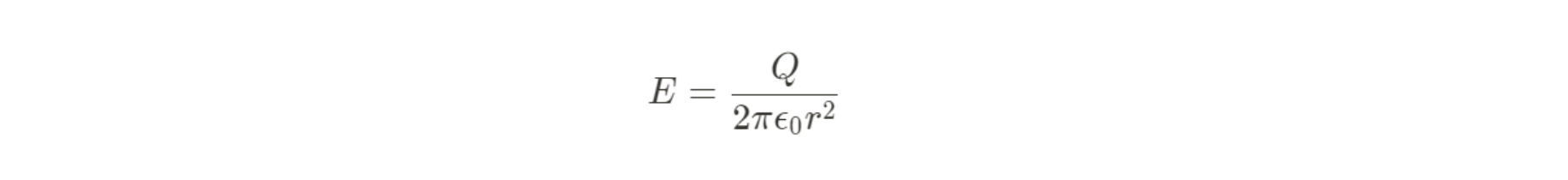
Imagine wrapping the point or hoop in a sphere. Then use A = 4πr^2.
Sphere (not fully enclosed):
** Note for Spheres: The electric field inside a uniformly charged sphere is proportional to r until r = R, then it behaves as an inverse square.**
Image Courtesy of phys.libretexts.org (CC BY 4.0)
Insulating Sheet of Charge:
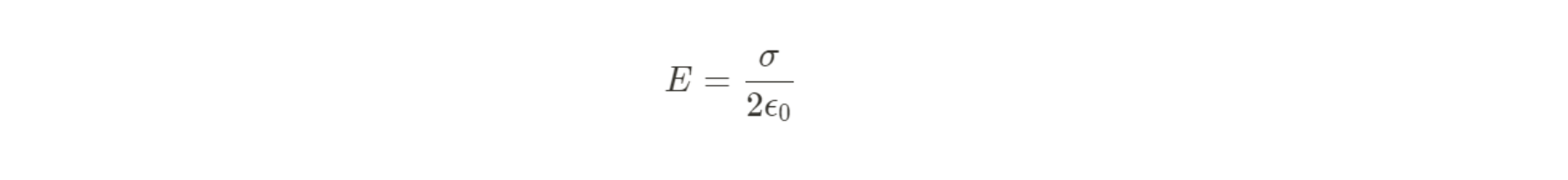
Enclose the sheet in a rectangle, being careful because there are fields on both side of the sheet. Use area charge density σ = Q/A --> q_enc = σA and E∲dA=2EA.
Potential Difference for a Variety of Shapes
This is more straightforward. For all the shapes, simply apply Gauss' Law to find an expression for E, then plug that into
Line of Charge Example:
Conducting Sheets Example (moving from the sheet to a distance d away):
Practice Questions
1.
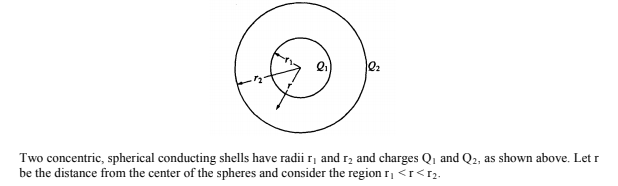
a)
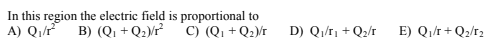
b)
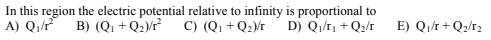
Image from collegeboard.org
Answer:
(a) The shells are conducting so the charge is only on their surfaces. Since we're in the region between r1 and r2, we fully enclose Q1. Using Gauss' Law, A is the correct answer.
(b) Relative to infinity, the total potential at r2 is V = k(Q1 + Q2)/r2, when we're between the sphere, we no longer have a change due to V_Q2 because the potential is CONSTANT inside of a conductor (while the Electric Field is zero -- this is an important thing to remember for the AP exam!). However, V_Q1 still varies according to 1/r. This means that E will be the correct answer.
2.

Image from collegeboard.org
Answer:
Choice B Is correct. Every point is equidistant from a given x value so V = kQ/r where r =√x^2 + a^2
3.
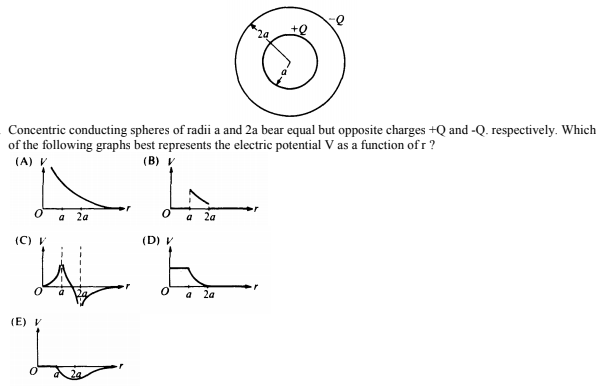
Image from collegeboard.org
Answer:
D is correct. Outside the spheres E = 0 since the total charge enclosed is 0. Inside the negative shell, the potential looks like a positively charged sphere (constant when r < a, and proportional to 1/r when r > a).
Practice FRQ
(courtesy of the College Board website, AP Physics C: Electricity + Magnetism 2007 Free Response Section, Question #2)

In the figure above, a nonconducting solid sphere of radius a with charge +Q uniformly distributed throughout its volume is concentric with a nonconducting spherical shell of inner radius 2a and outer radius 3a that has a charge -Q uniformly distributed throughout its volume. Express all answers in terms of the given quantities and fundamental constants.
(a) Using Gauss’s law, derive expressions for the magnitude of the electric field as a function of radius r in the following regions.
i. Within the solid sphere (r < a)
ii. Between the solid sphere and the spherical shell (a < r < 2a)
iii. Within the spherical shell (2a < r < 3a)
iv. Outside the spherical shell (r > 3a)
(b) What is the electric potential at the outer surface of the spherical shell (r = 3a)? Explain your reasoning.
(c) Derive an expression for the electric potential difference V_X - V_Y between points X and Y shown in the figure.
Scoring Guidelines
The scoring guidelines are located at this PDF from the College Board website for Question #2.
<< Hide Menu
1.5 Other Charge Distributions - Fields & Potentials
4 min read•june 18, 2024
Peter Apps
Peter Apps
This topic is a catch-all for more advanced applications of Charge Distributions, Gauss' Law, and calculating Electric Potentials. All of the concepts are covered in the previous sections, so if you need to, re-read those first.
Extended Charge Distributions
Up until now, we've dealt with charged objects as points, but sometimes we can't approximate the charge to be in a single location. These extended charge distributions are cases where the charge is in a ring, or line, or sheet.
The proccess for tackling all of these are very similar. We're going to chunk the total charge Q into into pieces, dq, which each contributes a partial field, dE. The entire equation is dE = k dq/r^2 * r, where r is the radius vector. By integrating that equation, we can sum up all of the dq which sums all of the dE to find the total field E.
Ring of Charge Example:

Image from dev.physicslab.org
If we assume that x >>> a, then we get the same result as for a point charge we found in Section 1. 2! This is a more general case, but we can see that it simplifies to the basic case!
Line of Charge Example:

Image created by author
Start by finding dq in terms of y using linear charge density ƛ.

Then, plug into our integral just like in the previous example. In this case, we can find r by using the pythagoreon theorem between y and x.
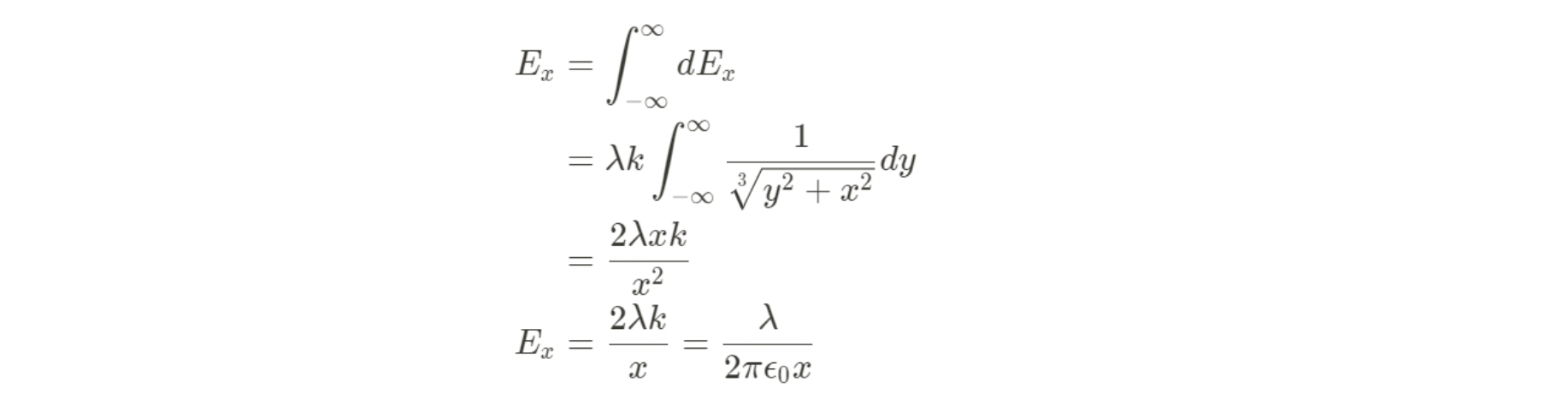
Gauss' Law for Various Shapes
You should be able to use Gauss' Law to derive these if you need to. Check out hyperphysics for more info.
Line of Charge:
Imagine enclosing the line of charge in a cylinder, use linear charge density λ = Q/L to find the enclosed charge, and then use A=2πrL.
Point, Hoop, or Sphere (fully enclosed):
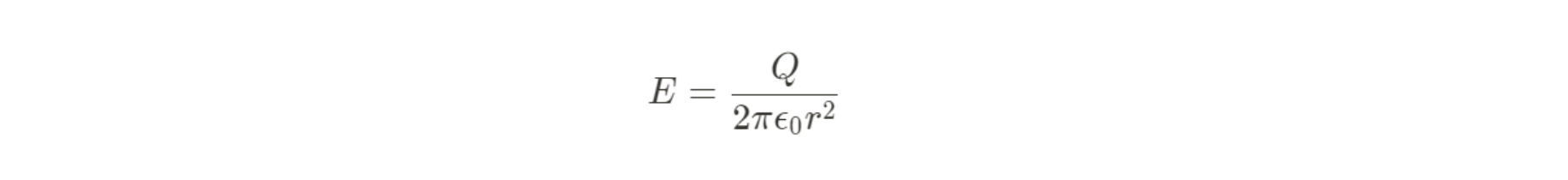
Imagine wrapping the point or hoop in a sphere. Then use A = 4πr^2.
Sphere (not fully enclosed):
** Note for Spheres: The electric field inside a uniformly charged sphere is proportional to r until r = R, then it behaves as an inverse square.**
Image Courtesy of phys.libretexts.org (CC BY 4.0)
Insulating Sheet of Charge:
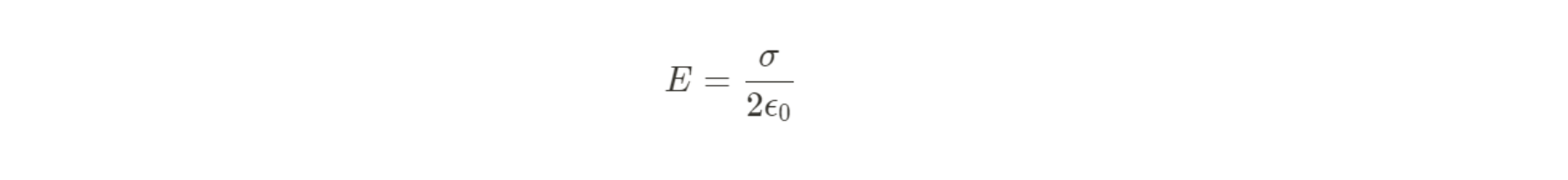
Enclose the sheet in a rectangle, being careful because there are fields on both side of the sheet. Use area charge density σ = Q/A --> q_enc = σA and E∲dA=2EA.
Potential Difference for a Variety of Shapes
This is more straightforward. For all the shapes, simply apply Gauss' Law to find an expression for E, then plug that into
Line of Charge Example:
Conducting Sheets Example (moving from the sheet to a distance d away):
Practice Questions
1.

a)
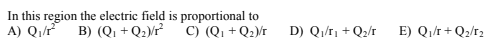
b)
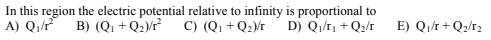
Image from collegeboard.org
Answer:
(a) The shells are conducting so the charge is only on their surfaces. Since we're in the region between r1 and r2, we fully enclose Q1. Using Gauss' Law, A is the correct answer.
(b) Relative to infinity, the total potential at r2 is V = k(Q1 + Q2)/r2, when we're between the sphere, we no longer have a change due to V_Q2 because the potential is CONSTANT inside of a conductor (while the Electric Field is zero -- this is an important thing to remember for the AP exam!). However, V_Q1 still varies according to 1/r. This means that E will be the correct answer.
2.

Image from collegeboard.org
Answer:
Choice B Is correct. Every point is equidistant from a given x value so V = kQ/r where r =√x^2 + a^2
3.

Image from collegeboard.org
Answer:
D is correct. Outside the spheres E = 0 since the total charge enclosed is 0. Inside the negative shell, the potential looks like a positively charged sphere (constant when r < a, and proportional to 1/r when r > a).
Practice FRQ
(courtesy of the College Board website, AP Physics C: Electricity + Magnetism 2007 Free Response Section, Question #2)

In the figure above, a nonconducting solid sphere of radius a with charge +Q uniformly distributed throughout its volume is concentric with a nonconducting spherical shell of inner radius 2a and outer radius 3a that has a charge -Q uniformly distributed throughout its volume. Express all answers in terms of the given quantities and fundamental constants.
(a) Using Gauss’s law, derive expressions for the magnitude of the electric field as a function of radius r in the following regions.
i. Within the solid sphere (r < a)
ii. Between the solid sphere and the spherical shell (a < r < 2a)
iii. Within the spherical shell (2a < r < 3a)
iv. Outside the spherical shell (r > 3a)
(b) What is the electric potential at the outer surface of the spherical shell (r = 3a)? Explain your reasoning.
(c) Derive an expression for the electric potential difference V_X - V_Y between points X and Y shown in the figure.
Scoring Guidelines
The scoring guidelines are located at this PDF from the College Board website for Question #2.

© 2024 Fiveable Inc. All rights reserved.