Browse By Unit
Daniella Garcia-Loos
Daniella Garcia-Loos
Translational VS Rotational Kinematics
Rotational kinematics is the branch of mechanics that deals with the motion of an object as it rotates around an axis. It is concerned with the description of an object's rotation and the variables that describe it, such as angular position, angular velocity, and angular acceleration.
In rotational kinematics, the position of an object is described in terms of its angular displacement, which is the angle through which the object has rotated from a reference position. The angular velocity of an object is the rate of change of its angular displacement over time, and is measured in units of radians per second. The angular acceleration of an object is the rate of change of its angular velocity over time, and is measured in units of radians per second squared.
Rotational kinematics also deals with the moment of inertia and torque, which are important concepts in understanding rotational motion. The moment of inertia of an object is a measure of its resistance to rotational motion, and depends on the distribution of mass around the axis of rotation. Torque is the rotational equivalent of force and it is the rotational force that causes rotational motion.
Objects can move rotationally and translationally! So we need to find ways to describe both. Δ𝛳 is the change in the angular position, in radians, and is the rotational analog for displacement Δx ѡ is angular velocity in the units radians per second, and is the rotational analog for velocity(v). ɑ is angular acceleration in the units of radians per second squared and is the rotational analog for acceleration(a).
You may notice that there's no such thing as angular time here, which is great for us as it's one of the ways we can tie these two worlds together with something other than radius!
Translational vs. Rotational:
- Translational kinematics is the branch of mechanics that deals with the motion of an object in a straight line, and can be described using position, velocity, and acceleration.
- Rotational kinematics is the branch of mechanics that deals with the motion of an object as it rotates around an axis, and can be described using angular position, angular velocity, and angular acceleration.
- In translational kinematics, distance and displacement are used to describe position, while in rotational kinematics, angle and angular displacement are used.
- In translational kinematics, linear velocity and acceleration are used, while in rotational kinematics, angular velocity and acceleration are used.
- To calculate the translational motion, you use the equations of motion such as v = u + at and s = ut + 1/2at^2. To calculate the rotational motion, you use the equations of motion such as w = w0 + αt and θ = θ0 + w0t + 1/2αt^2
- Translational kinematics deals with the object movement in a straight line. Rotational kinematics deals with the object rotation around a fixed axis, it also deals with the moment of inertia and torque.
- Translational kinematics is the study of linear motion, and it is concerned with the displacement, velocity and acceleration of the object. Rotational kinematics is the study of rotational motion, and it is concerned with angular displacement, angular velocity and angular acceleration of the object.
Below we can see the comparisons between translational and rotational motion, and you may notice things are eerily similar.
Translational Formulas:
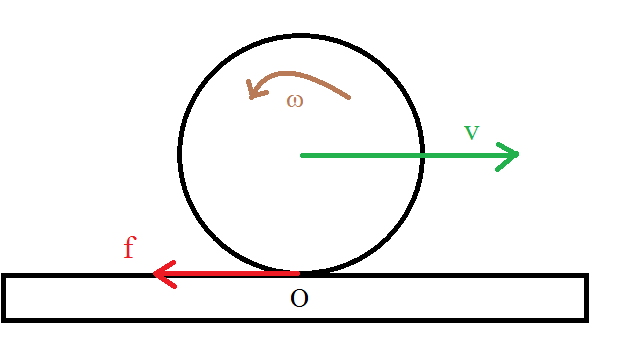
The formulas that work for both, other than the last one, require the object to be rolling without slipping, which essentially means that there is a torque on the object. For example, look at the picture below:
Practice Questions
- Large freight trains accelerate very slowly. Suppose one such train accelerates from rest, giving its 0.350-m-radius wheels an angular acceleration of 0.250 rad/s2. After the wheels have made 200 revolutions (assume no slippage): (a) How far has the train moved down the track? (b) What are the final angular velocity of the wheels and the linear velocity of the train? ([Taken from Lumen Learning)])
Part a:
Remember the equation between theta and radius: Δx=r𝛳
Suppose a yo-yo has a center shaft that has a 0.250 cm radius and that its string is being pulled.
(a) If the string is stationary and the yo-yo accelerates away from it at a rate of 1.50 m/s^2, what is the angular acceleration of the yo-yo?(b) What is the angular velocity after 0.750 s if it starts from rest?
<< Hide Menu
Daniella Garcia-Loos
Daniella Garcia-Loos
Translational VS Rotational Kinematics
Rotational kinematics is the branch of mechanics that deals with the motion of an object as it rotates around an axis. It is concerned with the description of an object's rotation and the variables that describe it, such as angular position, angular velocity, and angular acceleration.
In rotational kinematics, the position of an object is described in terms of its angular displacement, which is the angle through which the object has rotated from a reference position. The angular velocity of an object is the rate of change of its angular displacement over time, and is measured in units of radians per second. The angular acceleration of an object is the rate of change of its angular velocity over time, and is measured in units of radians per second squared.
Rotational kinematics also deals with the moment of inertia and torque, which are important concepts in understanding rotational motion. The moment of inertia of an object is a measure of its resistance to rotational motion, and depends on the distribution of mass around the axis of rotation. Torque is the rotational equivalent of force and it is the rotational force that causes rotational motion.
Objects can move rotationally and translationally! So we need to find ways to describe both. Δ𝛳 is the change in the angular position, in radians, and is the rotational analog for displacement Δx ѡ is angular velocity in the units radians per second, and is the rotational analog for velocity(v). ɑ is angular acceleration in the units of radians per second squared and is the rotational analog for acceleration(a).
You may notice that there's no such thing as angular time here, which is great for us as it's one of the ways we can tie these two worlds together with something other than radius!
Translational vs. Rotational:
- Translational kinematics is the branch of mechanics that deals with the motion of an object in a straight line, and can be described using position, velocity, and acceleration.
- Rotational kinematics is the branch of mechanics that deals with the motion of an object as it rotates around an axis, and can be described using angular position, angular velocity, and angular acceleration.
- In translational kinematics, distance and displacement are used to describe position, while in rotational kinematics, angle and angular displacement are used.
- In translational kinematics, linear velocity and acceleration are used, while in rotational kinematics, angular velocity and acceleration are used.
- To calculate the translational motion, you use the equations of motion such as v = u + at and s = ut + 1/2at^2. To calculate the rotational motion, you use the equations of motion such as w = w0 + αt and θ = θ0 + w0t + 1/2αt^2
- Translational kinematics deals with the object movement in a straight line. Rotational kinematics deals with the object rotation around a fixed axis, it also deals with the moment of inertia and torque.
- Translational kinematics is the study of linear motion, and it is concerned with the displacement, velocity and acceleration of the object. Rotational kinematics is the study of rotational motion, and it is concerned with angular displacement, angular velocity and angular acceleration of the object.
Below we can see the comparisons between translational and rotational motion, and you may notice things are eerily similar.
Translational Formulas:
The formulas that work for both, other than the last one, require the object to be rolling without slipping, which essentially means that there is a torque on the object. For example, look at the picture below:

Practice Questions
- Large freight trains accelerate very slowly. Suppose one such train accelerates from rest, giving its 0.350-m-radius wheels an angular acceleration of 0.250 rad/s2. After the wheels have made 200 revolutions (assume no slippage): (a) How far has the train moved down the track? (b) What are the final angular velocity of the wheels and the linear velocity of the train? ([Taken from Lumen Learning)])
Part a:
Remember the equation between theta and radius: Δx=r𝛳
Suppose a yo-yo has a center shaft that has a 0.250 cm radius and that its string is being pulled.
(a) If the string is stationary and the yo-yo accelerates away from it at a rate of 1.50 m/s^2, what is the angular acceleration of the yo-yo?(b) What is the angular velocity after 0.750 s if it starts from rest?

© 2024 Fiveable Inc. All rights reserved.