Browse By Unit
9.4 Kirchhoff’s Junction Rule, Ohm’s Law (Resistors in Series and Parallel)
2 min read•june 18, 2024
Peter Apps
Peter Apps
As of 2021, College Board only tests Units 1-7 on the AP Physics 1 exam. This page's content will not be tested on the exam, but we kept it online for you all as a resource.
Enduring Understanding 5.C
The electric charge of a system is conserved.
Essential Knowledge 5.C.3
Kirchhoff’s junction rule describes the conservation of electric charge in electrical circuits. Since the charge is conserved, the current must be conserved at each junction in the circuit. Examples include circuits that combine resistors in series and parallel.
** For AP 1, you could have a series circuit with 1 parallel branch.
Kirchhoff's Junction Rule follows a similar logic process as the Loop Rule, except with using conservation of charge instead of energy. In the circuit, the charge must be conserved since it’s a closed system. The current (rate of charge transfer) must be the same going into and out of a junction since there’s nowhere for the charge to disappear or appear from.
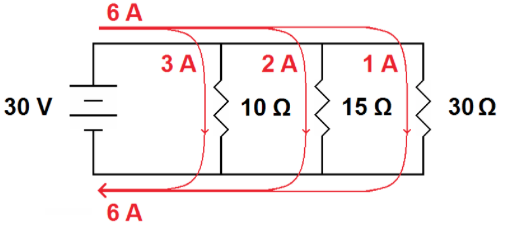
In the example below, the total current (6A) is split at each branch, then joined back as the branches merge again. The amount of current traveling through each branch is dependent on the resistance of the branch (more resistance = less current).
Both of Kirchhoff’s Laws together allow us to develop new equations for the equivalent resistance of series and parallel circuits. Here’s a quick overview of how these equations arise. For a more detailed explanation, check out this site.
Series Circuit: (1 Path)
For a series circuit, there’s only one path. Using the Junction Rule, this means that the current must be the same throughout the circuit. The Loop Rule says that the voltages must equal the battery’s voltage. Since V = IR (Ohm’s Law) that means that each voltage drop only depends on the resistance of the component. Therefore the total resistance of a series circuit must equal the sum of each of the individual resistances.
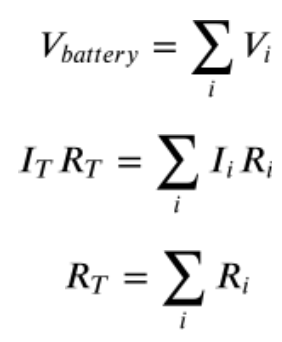
***** Big Idea ***** Adding another resistor in series will always INCREASE the equivalent resistance of the circuit.
Parallel Circuit: (2+ Paths)
For a parallel circuit, the voltage drop across each branch must be equal to the battery’s voltage (Loop Rule). The Junction Rule tells us that each loop has some fraction of the current related to the resistance, but the total current must be equal to the sum of each of the branches. Using Ohm’s Law (V = IR) we can expand then simplify our equation.
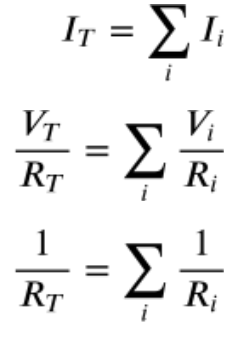
***** Big Idea ***** Adding another resistor in parallel will always DECREASE the equivalent resistance of the circuit.
🎥Watch: AP Physics 1 - Unit 9 Streams
<< Hide Menu
9.4 Kirchhoff’s Junction Rule, Ohm’s Law (Resistors in Series and Parallel)
2 min read•june 18, 2024
Peter Apps
Peter Apps
As of 2021, College Board only tests Units 1-7 on the AP Physics 1 exam. This page's content will not be tested on the exam, but we kept it online for you all as a resource.
Enduring Understanding 5.C
The electric charge of a system is conserved.
Essential Knowledge 5.C.3
Kirchhoff’s junction rule describes the conservation of electric charge in electrical circuits. Since the charge is conserved, the current must be conserved at each junction in the circuit. Examples include circuits that combine resistors in series and parallel.
** For AP 1, you could have a series circuit with 1 parallel branch.
Kirchhoff's Junction Rule follows a similar logic process as the Loop Rule, except with using conservation of charge instead of energy. In the circuit, the charge must be conserved since it’s a closed system. The current (rate of charge transfer) must be the same going into and out of a junction since there’s nowhere for the charge to disappear or appear from.
In the example below, the total current (6A) is split at each branch, then joined back as the branches merge again. The amount of current traveling through each branch is dependent on the resistance of the branch (more resistance = less current).

Both of Kirchhoff’s Laws together allow us to develop new equations for the equivalent resistance of series and parallel circuits. Here’s a quick overview of how these equations arise. For a more detailed explanation, check out this site.
Series Circuit: (1 Path)
For a series circuit, there’s only one path. Using the Junction Rule, this means that the current must be the same throughout the circuit. The Loop Rule says that the voltages must equal the battery’s voltage. Since V = IR (Ohm’s Law) that means that each voltage drop only depends on the resistance of the component. Therefore the total resistance of a series circuit must equal the sum of each of the individual resistances.
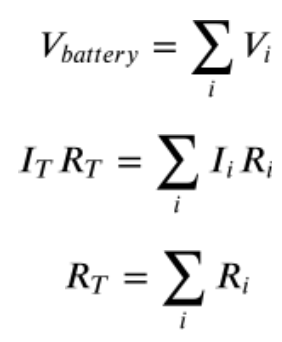
***** Big Idea ***** Adding another resistor in series will always INCREASE the equivalent resistance of the circuit.
Parallel Circuit: (2+ Paths)
For a parallel circuit, the voltage drop across each branch must be equal to the battery’s voltage (Loop Rule). The Junction Rule tells us that each loop has some fraction of the current related to the resistance, but the total current must be equal to the sum of each of the branches. Using Ohm’s Law (V = IR) we can expand then simplify our equation.
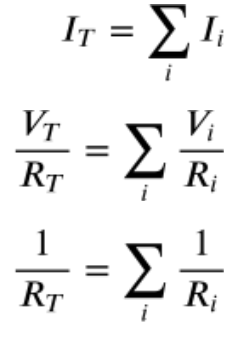
***** Big Idea ***** Adding another resistor in parallel will always DECREASE the equivalent resistance of the circuit.
🎥Watch: AP Physics 1 - Unit 9 Streams

© 2024 Fiveable Inc. All rights reserved.