Browse By Unit
7.2 Torque and Angular Acceleration
6 min read•june 18, 2024
Peter Apps
Kashvi Panjolia
Peter Apps
Kashvi Panjolia
Enduring Understanding 3.F
A force exerted on an object can cause a torque on that object.
Essential Knowledge 3.F.1
Only the force component perpendicular to the line connecting the axis of rotation and the point of application of the force results in a torque about that axis.
Essential Knowledge 3.F.2
The presence of a net torque along any axis will cause a rigid system to change its rotational motion or an object to change its rotational motion about that axis.
Torque
Torque is the rotational equivalent to a force. A net torque applied on an object will cause the object to change its rotational motion. The torque depends on 3 factors:
- The amount of force applied to the object
- The distance from the pivot point (axis of rotation) that the force is applied
- The angle between the radius vector and the force vector. Only the perpendicular part of the force can exert a torque on the object.
The torque on an object can be calculated by using the equation:

Where 𝜏 (the Greek letter tau) represents the torque, F is the applied force, r is the distance from the pivot the force is applied at, and θ is the angle between the r and F vectors when they are placed tail-to-tail. Torque is measured in Newton-meters (Nm).

Image courtesy of MIT Scripts.
A great way to understand the concept of torque is by using the example of opening a door. F3 in the image above pushes on a door at the end farthest from its hinge, which is the door's axis of rotation, and the normal way to open a door. If you pushed on a door close to its hinges, on a spot between F2 and F3, it would take a lot more force from you to open the door. As the image shows, F1 and F2 do not produce torques because they act towards the axis of rotation, and if you tried opening a door these ways, you would be stuck inside for a long time.🚪
** Important: Any force that acts towards the axis of rotation will not produce a torque, no matter how far away it is from the axis of rotation. **
This statement can be proved by using the equation for torque shown above. The angle θ between the force vector and the radius vector will be 180 degrees for both F1 and F2, since the r vector starts at the axis of rotation and ends at the point the force is applied at. A quick trip to the calculator will tell you that the sine of 180 degrees, which is used in the formula rFsinθ for torque, is 0. Using the mathematical principle that anything multiplied by 0 is 0, the torque F1 and F2 will produce is, you guessed it, 0 Nm. 0️⃣
The same methodology can be applied to make a claim that a torque produced at a 90-degree angle to the axis of rotation (and applied at the farthest distance from the axis as possible) will be the largest torque that can be produced with a certain amount of force for that object. Using rFsinθ for torque, if the angle θ between the force vector and the radius vector is 90 degrees, the sine of θ will be the sine of 90 degrees, which is 1. If you know your trigonometry, you'll recognize that 1 is the highest value possible for the sine of any angle, so a certain force that acts at a 90-degree angle to the axis of rotation and at the farthest distance possible will have the highest torque possible for that force, compared to other positions the force could be applied at on the object.
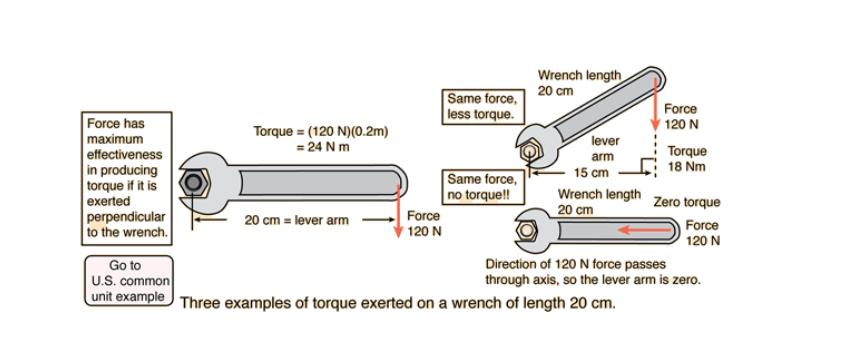
Another way to visualize torque. Image courtesy of Hyperphysics.
If all the torques on an object are balanced (∑𝜏=0), then the object is in rotational equilibrium.
Example:
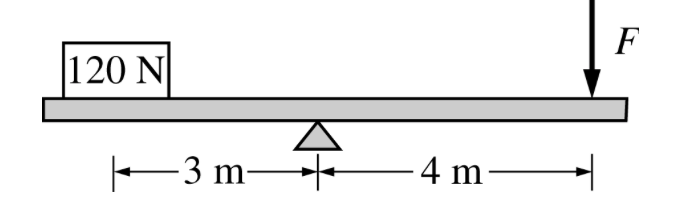
An object weighing 120 N is set on a rigid beam of negligible mass at a distance of 3 m from a pivot, as shown above. A vertical force is to be applied to the other end of the beam at a distance of 4 m away from the pivot to keep the beam at rest and horizontal. What is the magnitude F of the force required?
STEP 1: Identify all the forces in the diagram that could cause a torque
- Weight of the package → This force could cause a torque because the force is perpendicular and is 3m from the pivot. The torque will make the beam rotate counter-clockwise (CCW).
- Applied Force → This force could also cause a torque because it is perpendicular and is 4m from the pivot. The torque will make the beam rotate clockwise (CW).
STEP 2: Since the beam must remain at rest and horizontal, the two torques must cancel each other out. Set up the equation by setting the two torques equal to each other, substitute in your known variables, and solve for F.
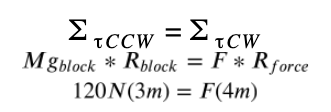
Your final answer should be F = 90N.
Note: Torque can be negative! The clockwise direction is considered the negative direction for torque, while counter-clockwise is considered the positive direction. This is counter-intuitive, so make sure you understand this concept. The magnitude, or absolute value, of the torque, however, will always be positive.
Moment of Inertia (I)
The object’s angular acceleration depends on the Moment of Inertia (I). The moment of inertia is the rotational equivalent of mass and describes how difficult it is to rotate an object. It also describes how the mass of an object is distributed across the object. For AP Physics 1, you will not need to derive moments of inertia for complex objects, although for AP Physics C you will need to. For a list of common moments of inertia, check out this link.
The moment of inertia for a point mass can be derived using the equation:
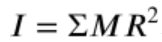
In general, the closer the masses are to the pivot point, the easier it is to rotate the object. In the example below, when the skater’s arms are outstretched, the radius of where the mass is on the skater is greater than if the skater's arms were at their sides, so the skater has a higher moment of inertia using the formula above. This means the skater is more difficult to rotate. When they bring their arms inwards, the radius of where the mass is on the skater decreases, so the moment of inertia decreases, and the skater is easier to rotate. ⛸
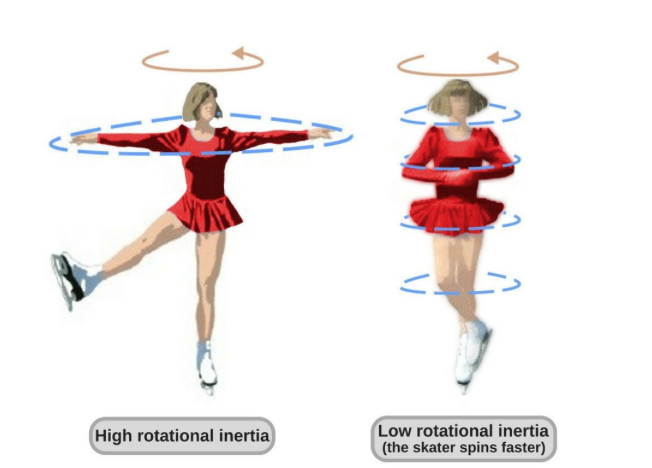
Image courtesy of ScienceABC.
Angular Acceleration
If there is an unbalanced torque, meaning the net torque is not equal to 0 (∑𝜏 ≠ 0), then the object will have an angular acceleration. The angular acceleration is the rotational equivalent of linear acceleration and measures the change in angular velocity. The angular acceleration can be found using the equation:
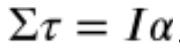
Does this equation look familiar? It should, because this is Newton's Second Law for Rotation, and the rotational equivalent to F=ma. This law states the net torque is equal to the product of the moment of inertia (I) and the angular acceleration (represented by the Greek letter α). This equation can be rearranged to solve for α:
α = ∑𝜏/I
EXAMPLE:

A uniform rod of length L and mass M is attached at one end to a frictionless pivot and is free to rotate. The rod is released from rest in the horizontal position. What is the initial angular acceleration of the rod? The moment of inertia of a rod rotated about its end is ⅓ *ML^*2.
STEP 1: Identify all the forces in the diagram that could cause a torque
- Weight of the rod → This force can generate a torque because the force is perpendicular to the axis of rotation (about the pivot, not the center of the rod) and is 3m from the pivot. Notice that the force acts at the center of the rod, not on the end.
STEP 2: Substitute known values into Newton's Second Law for Rotation. On the left, we substituted in values for rFsinθ to compute the net torque. The force acts at an angle of 90 degrees to the axis of rotation, and the sine of 90 degrees is 1, so sinθ was not shown.
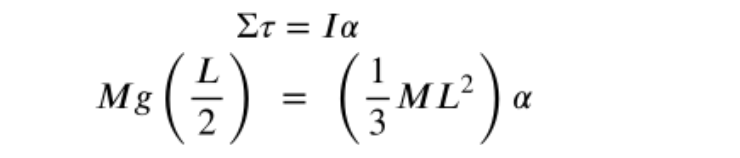
Your final answer should be:
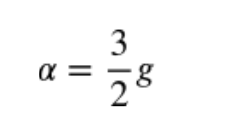
Note: Torques can also convert potential or translational kinetic energy into rotational kinetic energy. This is covered in the Unit 4: Energy study guide.
🎥Watch: AP Physics 1 - Unit 7 Streams
<< Hide Menu
7.2 Torque and Angular Acceleration
6 min read•june 18, 2024
Peter Apps
Kashvi Panjolia
Peter Apps
Kashvi Panjolia
Enduring Understanding 3.F
A force exerted on an object can cause a torque on that object.
Essential Knowledge 3.F.1
Only the force component perpendicular to the line connecting the axis of rotation and the point of application of the force results in a torque about that axis.
Essential Knowledge 3.F.2
The presence of a net torque along any axis will cause a rigid system to change its rotational motion or an object to change its rotational motion about that axis.
Torque
Torque is the rotational equivalent to a force. A net torque applied on an object will cause the object to change its rotational motion. The torque depends on 3 factors:
- The amount of force applied to the object
- The distance from the pivot point (axis of rotation) that the force is applied
- The angle between the radius vector and the force vector. Only the perpendicular part of the force can exert a torque on the object.
The torque on an object can be calculated by using the equation:

Where 𝜏 (the Greek letter tau) represents the torque, F is the applied force, r is the distance from the pivot the force is applied at, and θ is the angle between the r and F vectors when they are placed tail-to-tail. Torque is measured in Newton-meters (Nm).

Image courtesy of MIT Scripts.
A great way to understand the concept of torque is by using the example of opening a door. F3 in the image above pushes on a door at the end farthest from its hinge, which is the door's axis of rotation, and the normal way to open a door. If you pushed on a door close to its hinges, on a spot between F2 and F3, it would take a lot more force from you to open the door. As the image shows, F1 and F2 do not produce torques because they act towards the axis of rotation, and if you tried opening a door these ways, you would be stuck inside for a long time.🚪
** Important: Any force that acts towards the axis of rotation will not produce a torque, no matter how far away it is from the axis of rotation. **
This statement can be proved by using the equation for torque shown above. The angle θ between the force vector and the radius vector will be 180 degrees for both F1 and F2, since the r vector starts at the axis of rotation and ends at the point the force is applied at. A quick trip to the calculator will tell you that the sine of 180 degrees, which is used in the formula rFsinθ for torque, is 0. Using the mathematical principle that anything multiplied by 0 is 0, the torque F1 and F2 will produce is, you guessed it, 0 Nm. 0️⃣
The same methodology can be applied to make a claim that a torque produced at a 90-degree angle to the axis of rotation (and applied at the farthest distance from the axis as possible) will be the largest torque that can be produced with a certain amount of force for that object. Using rFsinθ for torque, if the angle θ between the force vector and the radius vector is 90 degrees, the sine of θ will be the sine of 90 degrees, which is 1. If you know your trigonometry, you'll recognize that 1 is the highest value possible for the sine of any angle, so a certain force that acts at a 90-degree angle to the axis of rotation and at the farthest distance possible will have the highest torque possible for that force, compared to other positions the force could be applied at on the object.

Another way to visualize torque. Image courtesy of Hyperphysics.
If all the torques on an object are balanced (∑𝜏=0), then the object is in rotational equilibrium.
Example:

An object weighing 120 N is set on a rigid beam of negligible mass at a distance of 3 m from a pivot, as shown above. A vertical force is to be applied to the other end of the beam at a distance of 4 m away from the pivot to keep the beam at rest and horizontal. What is the magnitude F of the force required?
STEP 1: Identify all the forces in the diagram that could cause a torque
- Weight of the package → This force could cause a torque because the force is perpendicular and is 3m from the pivot. The torque will make the beam rotate counter-clockwise (CCW).
- Applied Force → This force could also cause a torque because it is perpendicular and is 4m from the pivot. The torque will make the beam rotate clockwise (CW).
STEP 2: Since the beam must remain at rest and horizontal, the two torques must cancel each other out. Set up the equation by setting the two torques equal to each other, substitute in your known variables, and solve for F.
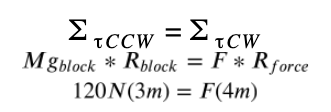
Your final answer should be F = 90N.
Note: Torque can be negative! The clockwise direction is considered the negative direction for torque, while counter-clockwise is considered the positive direction. This is counter-intuitive, so make sure you understand this concept. The magnitude, or absolute value, of the torque, however, will always be positive.
Moment of Inertia (I)
The object’s angular acceleration depends on the Moment of Inertia (I). The moment of inertia is the rotational equivalent of mass and describes how difficult it is to rotate an object. It also describes how the mass of an object is distributed across the object. For AP Physics 1, you will not need to derive moments of inertia for complex objects, although for AP Physics C you will need to. For a list of common moments of inertia, check out this link.
The moment of inertia for a point mass can be derived using the equation:
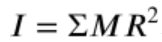
In general, the closer the masses are to the pivot point, the easier it is to rotate the object. In the example below, when the skater’s arms are outstretched, the radius of where the mass is on the skater is greater than if the skater's arms were at their sides, so the skater has a higher moment of inertia using the formula above. This means the skater is more difficult to rotate. When they bring their arms inwards, the radius of where the mass is on the skater decreases, so the moment of inertia decreases, and the skater is easier to rotate. ⛸

Image courtesy of ScienceABC.
Angular Acceleration
If there is an unbalanced torque, meaning the net torque is not equal to 0 (∑𝜏 ≠ 0), then the object will have an angular acceleration. The angular acceleration is the rotational equivalent of linear acceleration and measures the change in angular velocity. The angular acceleration can be found using the equation:
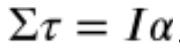
Does this equation look familiar? It should, because this is Newton's Second Law for Rotation, and the rotational equivalent to F=ma. This law states the net torque is equal to the product of the moment of inertia (I) and the angular acceleration (represented by the Greek letter α). This equation can be rearranged to solve for α:
α = ∑𝜏/I
EXAMPLE:

A uniform rod of length L and mass M is attached at one end to a frictionless pivot and is free to rotate. The rod is released from rest in the horizontal position. What is the initial angular acceleration of the rod? The moment of inertia of a rod rotated about its end is ⅓ *ML^*2.
STEP 1: Identify all the forces in the diagram that could cause a torque
- Weight of the rod → This force can generate a torque because the force is perpendicular to the axis of rotation (about the pivot, not the center of the rod) and is 3m from the pivot. Notice that the force acts at the center of the rod, not on the end.
STEP 2: Substitute known values into Newton's Second Law for Rotation. On the left, we substituted in values for rFsinθ to compute the net torque. The force acts at an angle of 90 degrees to the axis of rotation, and the sine of 90 degrees is 1, so sinθ was not shown.
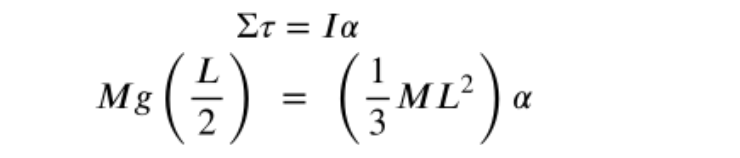
Your final answer should be:
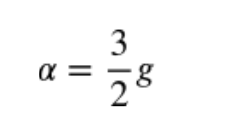
Note: Torques can also convert potential or translational kinetic energy into rotational kinetic energy. This is covered in the Unit 4: Energy study guide.
🎥Watch: AP Physics 1 - Unit 7 Streams

© 2024 Fiveable Inc. All rights reserved.