Browse By Unit
Peter Apps
Kashvi Panjolia
Peter Apps
Kashvi Panjolia
Learning Targets
All forces share certain common characteristics when considered by observers in inertial reference frames. An inertial reference frame is a frame of reference in which a body remains at rest or moves with constant linear velocity unless acted upon by forces.
An observer in a reference frame can describe the motion of an object using such quantities as position, displacement, distance, velocity, speed, and acceleration. For rotational motion, we define these quantities in terms of radians instead of meters.
The Radian

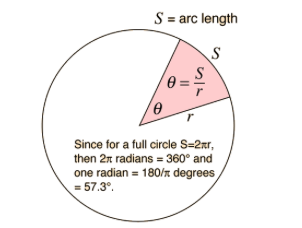
Imagine taking the radius of a circle and wrapping it around the circumference. It will create an angle whose arc length is equal to the radius. The angle that is created is 1 Radian.
An angle of 𝜋 radians would have an arc length of half the circumference (since the circumference is calculated using C=2𝜋r) and a full circumference would have an angle of 2𝜋 radians.
Basic Rotational Quantities
All the quantities below are the rotational analogs of linear quantities. Angular displacement corresponds with linear displacement, angular velocity corresponds with linear velocity, and so on.
Angular Displacement - represented by the angle 𝜃 in radians. Do not use degrees for the angular displacement. Any time you are given an angular displacement in degrees, convert to radians using radians = (degrees * 𝜋) / 180.
The angular displacement is calculated by subtracting the initial angular position from the final angular position:
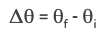
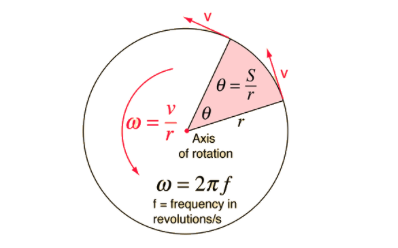
Angular Velocity - change in angular displacement over time, measured in radians per second (rad/s). It is represented by the Greek lowercase omega ω. It can also be calculated from the frequency of the object’s rotation, using the equation ω=2𝜋f. Sometimes, the angular velocity is given in revolutions per second (rev/s), which is another unit of measurement, but not the SI unit. To convert from revolutions to radians, you can remember that 1 revolution = 2𝜋 radians.
The angular velocity can be calculated by subtracting the initial angular position from the final angular position and putting that displacement over the time it took to go from the initial angular position to the final angular position:

Angular Acceleration - change in angular velocity over time, measured in radians per second squared (rad/s^2). It is represented by the Greek lowercase alpha α.
The angular acceleration can be calculated by subtracting the initial angular velocity from the final angular velocity and dividing that by the amount of time it took to change the velocity:
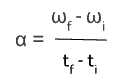
All of the linear terms can be related to their rotational term by the following equations (r = radius of the rotation). These are NOT on the reference table.

Angular displacement, angular velocity, and angular acceleration are all vector quantities, so they have both a magnitude and a direction. The frame of reference you choose will determine the direction of these quantities. A person looking at a spinning wheel from the front may say it is spinning clockwise, but a person looking at the same wheel from the back will say it is spinning counterclockwise. Usually, the question will tell you what direction to assume the rotation in, but it is important you understand this concept.
In rotational kinematics, the counterclockwise direction is the positive direction, while the clockwise direction is the negative direction. This is not intuitive, so make sure you learn this idea well. A disk spinning in the clockwise direction will have a negative angular velocity and a disk spinning in the counterclockwise direction will have a positive angular velocity.
Mathematical Representations of Motion
In kinematics, there are four major equations you must understand to begin calculations. They relate acceleration, displacement, initial and final velocity, and time together**.**

You may notice that these equations look very familiar. These are the rotational kinematics equations, and they follow the same format as the linear kinematics equations. Instead of x, these equations use θ. Instead of v, these equations use ω. The angular acceleration must be constant in the situation in order to use these rotational kinematics equations.
Variable Interpretation: Δ𝜃 is angular displacement in radians, 𝜔 is final angular velocity in radians/second, 𝜔o is initial angular velocity in radians/second, t is time in seconds, and 𝛼 is acceleration in rad/s^2.
⟶ In order to solve for a variable without having all four other quantities known, we look at the ‘Variable Missing’ column to pick the equation that best suits our question.
In linear kinematics, you learned the equation v=2𝜋r/T, where v is the linear velocity, r is the radius, and T is the period of the motion in seconds. Since v=ωr, we can rewrite this as ω=v/r. By dividing both sides by r in v=2𝜋r/T, we can establish a relationship between the angular velocity and the period: ω=2𝜋/T.

Practice Questions
1. An object is rotating with an angular velocity of 10 rad/s. After 5 seconds, what is the angular displacement of the object? a) 50 rad b) 25 rad c) 100 rad d) 0 rad
Answer: a) 50 rad Explanation: The angular displacement can be calculated using the equation Δθ = ω * Δt, where Δθ is the angular displacement, ω is the angular velocity, and Δt is the time. In this case, Δθ = 10 rad/s * 5 s = 50 rad.
2. A wheel starts at rest and accelerates uniformly to an angular velocity of 30 rad/s in 4 seconds. What is the angular acceleration of the wheel? a) 7.5 rad/s^2 b) 10 rad/s^2 c) 15 rad/s^2 d) 20 rad/s^2
Answer: a) 7.5 rad/s^2 Explanation: The angular acceleration can be calculated using the equation α = (ωf - ωi) / Δt, where α is the angular acceleration, ωf is the final angular velocity, ωi is the initial angular velocity, and Δt is the time. In this case, α = (30 rad/s - 0 rad/s) / 4 s = 7.5 rad/s^2.
3. A rotation starts at an angular velocity of 20 rad/s and slows down to an angular velocity of 10 rad/s over a time period of 2 seconds. What is the average angular acceleration of the rotation? a) -5 rad/s^2 b) 5 rad/s^2 c) -10 rad/s^2 d) 10 rad/s^2
Answer: a) -5 rad/s^2 Explanation: The average angular acceleration can be calculated using the equation α = (ωf - ωi) / Δt, where α is the angular acceleration, ωf is the final angular velocity, ωi is the initial angular velocity, and Δt is the time. In this case, α = (10 rad/s - 20 rad/s) / 2 s = -5 rad/s^2.
4. A disk with a radius of 0.5 meters is rotating with an angular velocity of 10 rad/s. What is the linear velocity of a point on the edge of the disk? a) 10 m/s b) 5 m/s c) 15 m/s d) 20 m/s
Answer: b) 5 m/s Explanation: The linear velocity of a point on the edge of the disk can be calculated using the equation v = r * ω, where v is the linear velocity, r is the radius of the disk, and ω is the angular velocity. In this case, v = 0.5 m * 10 rad/s = 5 m/s.
5. An object is rotating with an angular velocity of 15 rad/s. After 5 seconds, what is the final angular velocity of the object if it experiences a constant angular acceleration of -2 rad/s^2? a) 5 rad/s b) 10 rad/s c) 7 rad/s d) 12 rad/s
Answer: a) 5 rad/s Explanation: The final angular velocity can be calculated using the equation ωf = ωi + α*Δt, where ωf is the final angular velocity, ωi is the initial angular velocity, α is the angular acceleration, and Δt is the time. In this case, ωf = 15 rad/s + (-2 rad/s^2) * 5s = 15 rad/s - 10 rad/s = 5 rad/s
🎥Watch: AP Physics 1 - Unit 7 Streams
<< Hide Menu
Peter Apps
Kashvi Panjolia
Peter Apps
Kashvi Panjolia
Learning Targets
All forces share certain common characteristics when considered by observers in inertial reference frames. An inertial reference frame is a frame of reference in which a body remains at rest or moves with constant linear velocity unless acted upon by forces.
An observer in a reference frame can describe the motion of an object using such quantities as position, displacement, distance, velocity, speed, and acceleration. For rotational motion, we define these quantities in terms of radians instead of meters.
The Radian

Imagine taking the radius of a circle and wrapping it around the circumference. It will create an angle whose arc length is equal to the radius. The angle that is created is 1 Radian.
An angle of 𝜋 radians would have an arc length of half the circumference (since the circumference is calculated using C=2𝜋r) and a full circumference would have an angle of 2𝜋 radians.
Basic Rotational Quantities
All the quantities below are the rotational analogs of linear quantities. Angular displacement corresponds with linear displacement, angular velocity corresponds with linear velocity, and so on.
Angular Displacement - represented by the angle 𝜃 in radians. Do not use degrees for the angular displacement. Any time you are given an angular displacement in degrees, convert to radians using radians = (degrees * 𝜋) / 180.
The angular displacement is calculated by subtracting the initial angular position from the final angular position:
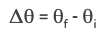

Angular Velocity - change in angular displacement over time, measured in radians per second (rad/s). It is represented by the Greek lowercase omega ω. It can also be calculated from the frequency of the object’s rotation, using the equation ω=2𝜋f. Sometimes, the angular velocity is given in revolutions per second (rev/s), which is another unit of measurement, but not the SI unit. To convert from revolutions to radians, you can remember that 1 revolution = 2𝜋 radians.
The angular velocity can be calculated by subtracting the initial angular position from the final angular position and putting that displacement over the time it took to go from the initial angular position to the final angular position:


Angular Acceleration - change in angular velocity over time, measured in radians per second squared (rad/s^2). It is represented by the Greek lowercase alpha α.
The angular acceleration can be calculated by subtracting the initial angular velocity from the final angular velocity and dividing that by the amount of time it took to change the velocity:
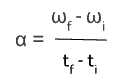
All of the linear terms can be related to their rotational term by the following equations (r = radius of the rotation). These are NOT on the reference table.

Angular displacement, angular velocity, and angular acceleration are all vector quantities, so they have both a magnitude and a direction. The frame of reference you choose will determine the direction of these quantities. A person looking at a spinning wheel from the front may say it is spinning clockwise, but a person looking at the same wheel from the back will say it is spinning counterclockwise. Usually, the question will tell you what direction to assume the rotation in, but it is important you understand this concept.
In rotational kinematics, the counterclockwise direction is the positive direction, while the clockwise direction is the negative direction. This is not intuitive, so make sure you learn this idea well. A disk spinning in the clockwise direction will have a negative angular velocity and a disk spinning in the counterclockwise direction will have a positive angular velocity.
Mathematical Representations of Motion
In kinematics, there are four major equations you must understand to begin calculations. They relate acceleration, displacement, initial and final velocity, and time together**.**

You may notice that these equations look very familiar. These are the rotational kinematics equations, and they follow the same format as the linear kinematics equations. Instead of x, these equations use θ. Instead of v, these equations use ω. The angular acceleration must be constant in the situation in order to use these rotational kinematics equations.
Variable Interpretation: Δ𝜃 is angular displacement in radians, 𝜔 is final angular velocity in radians/second, 𝜔o is initial angular velocity in radians/second, t is time in seconds, and 𝛼 is acceleration in rad/s^2.
⟶ In order to solve for a variable without having all four other quantities known, we look at the ‘Variable Missing’ column to pick the equation that best suits our question.
In linear kinematics, you learned the equation v=2𝜋r/T, where v is the linear velocity, r is the radius, and T is the period of the motion in seconds. Since v=ωr, we can rewrite this as ω=v/r. By dividing both sides by r in v=2𝜋r/T, we can establish a relationship between the angular velocity and the period: ω=2𝜋/T.

Practice Questions
1. An object is rotating with an angular velocity of 10 rad/s. After 5 seconds, what is the angular displacement of the object? a) 50 rad b) 25 rad c) 100 rad d) 0 rad
Answer: a) 50 rad Explanation: The angular displacement can be calculated using the equation Δθ = ω * Δt, where Δθ is the angular displacement, ω is the angular velocity, and Δt is the time. In this case, Δθ = 10 rad/s * 5 s = 50 rad.
2. A wheel starts at rest and accelerates uniformly to an angular velocity of 30 rad/s in 4 seconds. What is the angular acceleration of the wheel? a) 7.5 rad/s^2 b) 10 rad/s^2 c) 15 rad/s^2 d) 20 rad/s^2
Answer: a) 7.5 rad/s^2 Explanation: The angular acceleration can be calculated using the equation α = (ωf - ωi) / Δt, where α is the angular acceleration, ωf is the final angular velocity, ωi is the initial angular velocity, and Δt is the time. In this case, α = (30 rad/s - 0 rad/s) / 4 s = 7.5 rad/s^2.
3. A rotation starts at an angular velocity of 20 rad/s and slows down to an angular velocity of 10 rad/s over a time period of 2 seconds. What is the average angular acceleration of the rotation? a) -5 rad/s^2 b) 5 rad/s^2 c) -10 rad/s^2 d) 10 rad/s^2
Answer: a) -5 rad/s^2 Explanation: The average angular acceleration can be calculated using the equation α = (ωf - ωi) / Δt, where α is the angular acceleration, ωf is the final angular velocity, ωi is the initial angular velocity, and Δt is the time. In this case, α = (10 rad/s - 20 rad/s) / 2 s = -5 rad/s^2.
4. A disk with a radius of 0.5 meters is rotating with an angular velocity of 10 rad/s. What is the linear velocity of a point on the edge of the disk? a) 10 m/s b) 5 m/s c) 15 m/s d) 20 m/s
Answer: b) 5 m/s Explanation: The linear velocity of a point on the edge of the disk can be calculated using the equation v = r * ω, where v is the linear velocity, r is the radius of the disk, and ω is the angular velocity. In this case, v = 0.5 m * 10 rad/s = 5 m/s.
5. An object is rotating with an angular velocity of 15 rad/s. After 5 seconds, what is the final angular velocity of the object if it experiences a constant angular acceleration of -2 rad/s^2? a) 5 rad/s b) 10 rad/s c) 7 rad/s d) 12 rad/s
Answer: a) 5 rad/s Explanation: The final angular velocity can be calculated using the equation ωf = ωi + α*Δt, where ωf is the final angular velocity, ωi is the initial angular velocity, α is the angular acceleration, and Δt is the time. In this case, ωf = 15 rad/s + (-2 rad/s^2) * 5s = 15 rad/s - 10 rad/s = 5 rad/s
🎥Watch: AP Physics 1 - Unit 7 Streams

© 2024 Fiveable Inc. All rights reserved.