Browse By Unit
7.4 Conservation of Angular Momentum
5 min read•june 18, 2024
Peter Apps
Kashvi Panjolia
Peter Apps
Kashvi Panjolia
Enduring Understanding 5.E: The angular momentum of a system is conserved.
Essential Knowledge 5.E.1: If the net external torque exerted on the system is zero, the angular momentum of the system does not change.
Angular Momentum
Angular Momentum is the rotational equivalent to linear momentum and is calculated by using the equation L=Iω, where I is the moment of inertia and ω is the angular velocity. It is measured in units of kilogram meters squared per second (kgm^/s). Angular momentum is conserved when there are no net external torques on the object(s) in the system.

Image courtesy of ScienceABC.
The skater above has a constant angular momentum in both images. This means the overall angular momentum of the skater does not change from the first image to the second. The skater pulling their hands in is an internal force (and therefore an internal torque), so angular momentum is conserved. In terms of I and 𝜔, the first image has a large I and small 𝜔, since the skater's arms are extended outward, meaning more mass is distributed farther away from the axis of rotation, which goes through the center of the skater. If the skater has a higher rotational inertia, then the angular velocity ω will have to be smaller.
In the second image, the skater has a smaller I and larger 𝜔. The skater has pulled their arms and legs in, so more mass is closer to the axis of rotation. In the equation for moment of inertia, I=MR^2, this means that the moment of inertia will be smaller than before because the radius (R) decreases while the amount of total mass (M) stays the same. If the rotational inertia is smaller, the angular velocity will be larger to maintain constant angular momentum. Therefore, the skater is spinning faster in the second image.
Other common situations with the conservation of angular momentum involve collisions and planetary motion.
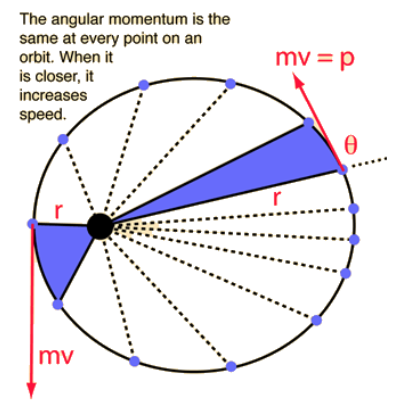
Angular momentum is conserved in planetary motion because the planets are moving in closed orbits around the sun. A closed orbit is when the planet moves in a repeated pattern and returns to the same point in space after a certain period of time, such as a planet orbiting a star. The moment of inertia of the planet is constant, as the planet is not changing its shape or size, and the angular velocity of the planet is also constant, as it is moving in a closed orbit.
The angular velocity is constant because of Kepler's 2nd Law, which states that planets sweep out equal areas (the purple regions in the image above) in equal amounts of time. In the purple region to the left, the planet still has the same angular velocity as it does when it passes through the purple region to the right. The planet has a greater linear velocity on the left, since it is closer to the center of the orbit (the star), and the gravitational pull is stronger there. However, the faster linear velocity is negated by the fact that the planet sweeps out a larger angle than in the purple region to the right. Since the time it takes to pass through the region is the same for both regions, the angular velocity of the planet is the same in both regions.
Note the difference between linear velocity and angular velocity. Linear velocity is the velocity that is directly related to distance and time, while angular velocity is the velocity that relates to angle and time. Kepler's 2nd Law tells us that the linear velocity of the planet changes but angular velocity does not change. Therefore, angular momentum is conserved. You do not need to know about Kepler's 2nd Law for the AP exam, but you do need to understand that the angular momentum of a planet in a closed orbit is conserved.
EXAMPLE: (AP Classroom)
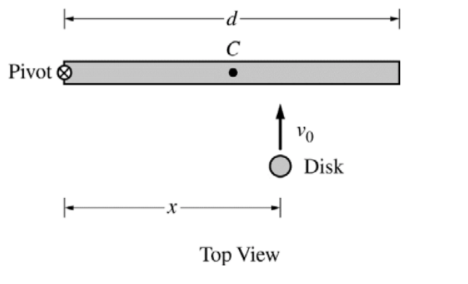
The left end of a rod of length d and rotational inertia I of the rod is attached to a frictionless horizontal surface by a frictionless pivot, as shown above. Point C marks the center (midpoint) of the rod. The rod is initially motionless but is free to rotate around the pivot. A student will slide a disk of mass:

toward the rod with velocity v0 perpendicular to the rod, and the disk will stick to the rod a distance x from the pivot.
a. Immediately before colliding with the rod, the disk’s rotational inertia about the pivot is:
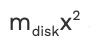
and its angular momentum with respect to the pivot is:

Derive an equation for the post-collision angular speed ω of the rod. Express your answer in terms of d, mdisk, I, x, v0, and physical constants, as appropriate.
STEP 1: Identify applicable equations -
- The question mentions angular momentum and angular speed. We may also need conservation of momentum because a collision is mentioned. Angular momentum can be calculated using L=Iω for the rod and L=mvr for the disk about the pivot point since the disk is moving in a straight-line motion.
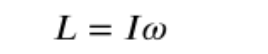
STEP 2: Set up your conservation of angular momentum. This statement is very similar to any other conservation statement you have written, such as for energy or linear momentum. Before the collision, the rod is at rest and the disk is the only object in the disk-rod system that is moving, so we only calculate the angular momentum of the disk on the left side of the equation. After the collision, the disk sticks to the rod and both objects move together with a final angular velocity ω, so we combine the moment of inertia for the two objects on the right. Now, we simply solve for ω by dividing both sides by the combined post-collision moment of inertia.

Your answer should be:
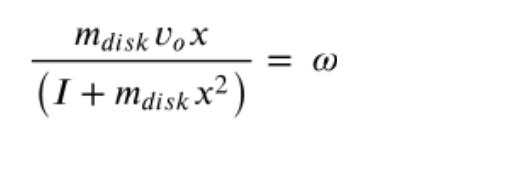
b. Consider the collision for which your equation in part (a) was derived, except now suppose the disk bounces backward off the rod instead of sticking to the rod. Is the post-collision angular speed of the rod when the disk bounces off it greater than, less than, or equal to the post-collision angular speed of the rod when the disk sticks to it?
_____Greater than _____Less than _____Equal to
Briefly explain your reasoning.
CORRECT ANSWER: Greater than
REASONING: When the disk hits the rod, it transfers angular momentum to the rod. This is an internal collision so angular momentum is conserved before and after the collision. When the disk bounces off the rod, its angular momentum changes from positive to negative. This is a larger change in its momentum than when it was brought to rest by sticking to the rod. Since the total momentum is constant, the rod must gain more angular momentum to balance out the now negative momentum of the disk. Since the rod has more angular momentum but the same moment of inertia, analyzing the equation L=Iω tells us that the angular velocity of the rod must increase to create the increase in angular momentum, so the final angular velocity will be greater than the original final angular velocity, when the disk stuck to the rod.
🎥Watch: AP Physics 1 - Unit 7 Streams
<< Hide Menu
7.4 Conservation of Angular Momentum
5 min read•june 18, 2024
Peter Apps
Kashvi Panjolia
Peter Apps
Kashvi Panjolia
Enduring Understanding 5.E: The angular momentum of a system is conserved.
Essential Knowledge 5.E.1: If the net external torque exerted on the system is zero, the angular momentum of the system does not change.
Angular Momentum
Angular Momentum is the rotational equivalent to linear momentum and is calculated by using the equation L=Iω, where I is the moment of inertia and ω is the angular velocity. It is measured in units of kilogram meters squared per second (kgm^/s). Angular momentum is conserved when there are no net external torques on the object(s) in the system.

Image courtesy of ScienceABC.
The skater above has a constant angular momentum in both images. This means the overall angular momentum of the skater does not change from the first image to the second. The skater pulling their hands in is an internal force (and therefore an internal torque), so angular momentum is conserved. In terms of I and 𝜔, the first image has a large I and small 𝜔, since the skater's arms are extended outward, meaning more mass is distributed farther away from the axis of rotation, which goes through the center of the skater. If the skater has a higher rotational inertia, then the angular velocity ω will have to be smaller.
In the second image, the skater has a smaller I and larger 𝜔. The skater has pulled their arms and legs in, so more mass is closer to the axis of rotation. In the equation for moment of inertia, I=MR^2, this means that the moment of inertia will be smaller than before because the radius (R) decreases while the amount of total mass (M) stays the same. If the rotational inertia is smaller, the angular velocity will be larger to maintain constant angular momentum. Therefore, the skater is spinning faster in the second image.
Other common situations with the conservation of angular momentum involve collisions and planetary motion.

Angular momentum is conserved in planetary motion because the planets are moving in closed orbits around the sun. A closed orbit is when the planet moves in a repeated pattern and returns to the same point in space after a certain period of time, such as a planet orbiting a star. The moment of inertia of the planet is constant, as the planet is not changing its shape or size, and the angular velocity of the planet is also constant, as it is moving in a closed orbit.
The angular velocity is constant because of Kepler's 2nd Law, which states that planets sweep out equal areas (the purple regions in the image above) in equal amounts of time. In the purple region to the left, the planet still has the same angular velocity as it does when it passes through the purple region to the right. The planet has a greater linear velocity on the left, since it is closer to the center of the orbit (the star), and the gravitational pull is stronger there. However, the faster linear velocity is negated by the fact that the planet sweeps out a larger angle than in the purple region to the right. Since the time it takes to pass through the region is the same for both regions, the angular velocity of the planet is the same in both regions.
Note the difference between linear velocity and angular velocity. Linear velocity is the velocity that is directly related to distance and time, while angular velocity is the velocity that relates to angle and time. Kepler's 2nd Law tells us that the linear velocity of the planet changes but angular velocity does not change. Therefore, angular momentum is conserved. You do not need to know about Kepler's 2nd Law for the AP exam, but you do need to understand that the angular momentum of a planet in a closed orbit is conserved.
EXAMPLE: (AP Classroom)

The left end of a rod of length d and rotational inertia I of the rod is attached to a frictionless horizontal surface by a frictionless pivot, as shown above. Point C marks the center (midpoint) of the rod. The rod is initially motionless but is free to rotate around the pivot. A student will slide a disk of mass:

toward the rod with velocity v0 perpendicular to the rod, and the disk will stick to the rod a distance x from the pivot.
a. Immediately before colliding with the rod, the disk’s rotational inertia about the pivot is:
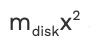
and its angular momentum with respect to the pivot is:

Derive an equation for the post-collision angular speed ω of the rod. Express your answer in terms of d, mdisk, I, x, v0, and physical constants, as appropriate.
STEP 1: Identify applicable equations -
- The question mentions angular momentum and angular speed. We may also need conservation of momentum because a collision is mentioned. Angular momentum can be calculated using L=Iω for the rod and L=mvr for the disk about the pivot point since the disk is moving in a straight-line motion.
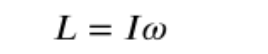
STEP 2: Set up your conservation of angular momentum. This statement is very similar to any other conservation statement you have written, such as for energy or linear momentum. Before the collision, the rod is at rest and the disk is the only object in the disk-rod system that is moving, so we only calculate the angular momentum of the disk on the left side of the equation. After the collision, the disk sticks to the rod and both objects move together with a final angular velocity ω, so we combine the moment of inertia for the two objects on the right. Now, we simply solve for ω by dividing both sides by the combined post-collision moment of inertia.

Your answer should be:
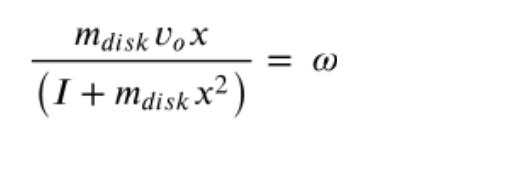
b. Consider the collision for which your equation in part (a) was derived, except now suppose the disk bounces backward off the rod instead of sticking to the rod. Is the post-collision angular speed of the rod when the disk bounces off it greater than, less than, or equal to the post-collision angular speed of the rod when the disk sticks to it?
_____Greater than _____Less than _____Equal to
Briefly explain your reasoning.
CORRECT ANSWER: Greater than
REASONING: When the disk hits the rod, it transfers angular momentum to the rod. This is an internal collision so angular momentum is conserved before and after the collision. When the disk bounces off the rod, its angular momentum changes from positive to negative. This is a larger change in its momentum than when it was brought to rest by sticking to the rod. Since the total momentum is constant, the rod must gain more angular momentum to balance out the now negative momentum of the disk. Since the rod has more angular momentum but the same moment of inertia, analyzing the equation L=Iω tells us that the angular velocity of the rod must increase to create the increase in angular momentum, so the final angular velocity will be greater than the original final angular velocity, when the disk stuck to the rod.
🎥Watch: AP Physics 1 - Unit 7 Streams

© 2024 Fiveable Inc. All rights reserved.