Browse By Unit
Peter Apps
Kashvi Panjolia
Peter Apps
Kashvi Panjolia
- Enduring Understanding 4.D- A net torque exerted on a system by other objects or systems will change the angular momentum of the system.
- Essential Knowledge 4.D.1- Torque, angular velocity, angular acceleration, and angular momentum are vectors and can be characterized as positive or negative depending on whether they give rise to or correspond to counterclockwise or clockwise rotation with respect to an axis.
- Essential Knowledge 4.D.2- The angular momentum of a system may change due to interactions with other objects or systems.
- Essential Knowledge 4.D.3- The change in angular momentum is given by the product of the average torque and the time interval during which the torque is exerted.
Angular Momentum
Angular momentum is the rotational equivalent of linear momentum. It is represented by the equation L=I𝜔 where L is the angular momentum, I is the moment of inertia of the object, and 𝜔 is the angular velocity of the object. In addition, the angular momentum of an object moving in a straight line relative to a fixed point can be found by multiplying its linear momentum (p) by the perpendicular distance (r) to the point as shown in the picture.
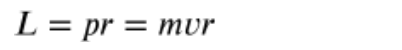
An object that is moving in a straight line can still have angular momentum if the angular momentum is calculated relative to a fixed point. This is because if you are standing at that fixed point and looking at an object moving past you, you will still have to turn your head to watch that object, which is the source of the angular momentum. For example, if you are standing at a train station and watch a train go by, you will first turn your head to the right (or left) to watch the train come in, then look straight ahead as the train stops at the station, and finally, turn your head to the left (or right) to watch the train leave. In this situation, the train has an angular momentum about a fixed point, which is your position on the platform. This angular momentum can be calculated using L=mvr, since you will usually not be given an angle value.
🎥Watch: Minutephysics - What is Angular Momentum?
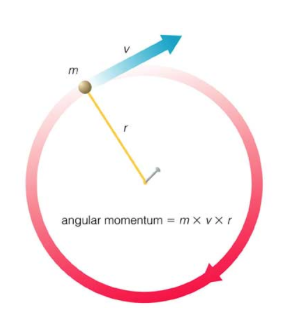
Image courtesy of MilesMathis.
Just like a force acting on an object causes a change in linear momentum, a net torque causes a change in the angular momentum of the object. Also, the change in linear momentum (impulse) of an object can be calculated by multiplying the net force exerted on the object by the amount of time the force was exerted. Similarly, the change in angular momentum of an object can be calculated by the net torque exerted on the object multiplied by the time interval for which the torque was exerted. The units for angular momentum are kilogram meters squared per second or kgm^2/s.
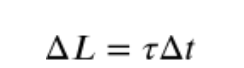
It is also important to note that the net angular momentum of a system is the vector sum of the angular momentum of each object in the system. This is because angular momentum is a vector quantity and follows the rules of vector addition. The total angular momentum of the system is the sum of all the individual angular momenta of the objects in the system, and the direction of the total angular momentum is determined by the directions of the individual angular momenta.
EXAMPLE: (AP Classroom)
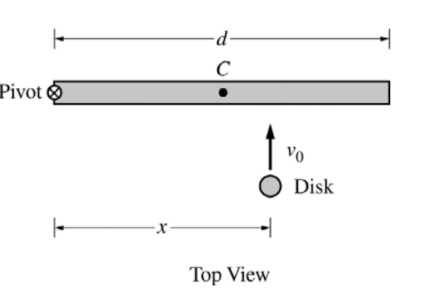
The left end of a rod of length d and rotational inertia I is attached to a frictionless horizontal surface by a frictionless pivot, as shown above. Point C marks the center (midpoint) of the rod. The rod is initially motionless but is free to rotate around the pivot.
A student will slide a disk of mass:

toward the rod with velocity v0 perpendicular to the rod, and the disk will stick to the rod a distance x from the pivot.
The student wants the rod-disk system to end up with as much angular speed as possible.

Briefly explain your reasoning without manipulating equations.
CORRECT ANSWER: To the right of C
REASONING: To make the largest angular speed, the rod needs to get the greatest angular momentum possible (L=I𝜔). To get the largest angular momentum, the rod must be given the greatest possible torque. Since torque depends on the moment of inertia and the angular acceleration (𝜏=Iα), and the moment of inertia is calculated using I=cMR^2 (where c is a constant depending on the object), hitting the rod at the greatest radius will produce the greatest torque. Because the pivot is on the left side of C, we want to hit on the right side of C to maximize the radius so the moment of inertia increases, causing the net torque to increase, which will increase the angular speed.
ALTERNATE EXPLANATION: To create the largest angular speed, the rod needs to get the greatest angular momentum possible (L=I𝜔). To do this, we want the disk to transfer the greatest amount of momentum to the rod. Since angular momentum is conserved in the rod-disk system (no outside torques), this means that we want the initial angular momentum of the disk to be as large as possible. The angular momentum of the disk is equal to L=mvr where r is the distance from the pivot because the disk is moving in a straight-line motion relative to the pivot point of the rod.
To make:
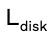
the largest it can possibly be, it needs to hit at the greatest distance away from the pivot to maximize the value of r. The greatest distance away from the pivot is on the right side of C.
(This explanation uses the law of conservation of momentum which will be covered in the next section.)
🎥Watch: AP Physics 1 - Unit 7 Streams
Practice Problems
1. A spinning disk has a mass of 0.5 kg and a radius of 0.2 m. The disk is spinning at an angular velocity of 2 rad/s. What is the angular momentum of the disk? (I = 1/2MR^2 for the disk)
A) 0.02 kgm^2/s B) 0.2 kgm^2/s C) 0.4 kgm^2/s D) 0.8 kgm^2/s
The solution is: L = Iω = (1/2) mr^2ω = (1/2)*0.5(*0.2^2)2 = 0.02 kgm^2/s
The answer is A) 0.02 kgm^2/s
2. A 0.4 kg ball is attached to a string of length 0.5 m and is rotating in a circle with an angular velocity of 3 rad/s. What is the angular momentum of the ball? (I= 2/5MR^2 for the ball)
A) 0.3 kgm^2/s B) 0.12 kgm^2/s C) 0.9 kgm^2/s D) 1.2 kgm^2/s
The solution is:
L = Iω = (2/5) mr^2ω = (2/5)*0.4(*0.5^2)3 = 0.12 kgm^2/s The answer is:
A) 0.12 kgm^2/s
3. A flywheel (disk) with a mass of 8 kg and a radius of 0.3 m is spinning at an angular velocity of 4 rad/s. What is the angular momentum of the flywheel? (I = 1/2MR^2 for the flywheel)
A) 1.44 kgm^2/s B) 2.4 kgm^2/s C) 4.8 kgm^2/s D) 9.6 kgm^2/s
The solution is:
L = Iω = (1/2) mr^2ω = (1/2)*8(*0.3^2)4 = 1.44 kgm^2/s The answer is
A) 1.44 kgm^2/s
<< Hide Menu
Peter Apps
Kashvi Panjolia
Peter Apps
Kashvi Panjolia
- Enduring Understanding 4.D- A net torque exerted on a system by other objects or systems will change the angular momentum of the system.
- Essential Knowledge 4.D.1- Torque, angular velocity, angular acceleration, and angular momentum are vectors and can be characterized as positive or negative depending on whether they give rise to or correspond to counterclockwise or clockwise rotation with respect to an axis.
- Essential Knowledge 4.D.2- The angular momentum of a system may change due to interactions with other objects or systems.
- Essential Knowledge 4.D.3- The change in angular momentum is given by the product of the average torque and the time interval during which the torque is exerted.
Angular Momentum
Angular momentum is the rotational equivalent of linear momentum. It is represented by the equation L=I𝜔 where L is the angular momentum, I is the moment of inertia of the object, and 𝜔 is the angular velocity of the object. In addition, the angular momentum of an object moving in a straight line relative to a fixed point can be found by multiplying its linear momentum (p) by the perpendicular distance (r) to the point as shown in the picture.
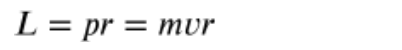
An object that is moving in a straight line can still have angular momentum if the angular momentum is calculated relative to a fixed point. This is because if you are standing at that fixed point and looking at an object moving past you, you will still have to turn your head to watch that object, which is the source of the angular momentum. For example, if you are standing at a train station and watch a train go by, you will first turn your head to the right (or left) to watch the train come in, then look straight ahead as the train stops at the station, and finally, turn your head to the left (or right) to watch the train leave. In this situation, the train has an angular momentum about a fixed point, which is your position on the platform. This angular momentum can be calculated using L=mvr, since you will usually not be given an angle value.
🎥Watch: Minutephysics - What is Angular Momentum?

Image courtesy of MilesMathis.
Just like a force acting on an object causes a change in linear momentum, a net torque causes a change in the angular momentum of the object. Also, the change in linear momentum (impulse) of an object can be calculated by multiplying the net force exerted on the object by the amount of time the force was exerted. Similarly, the change in angular momentum of an object can be calculated by the net torque exerted on the object multiplied by the time interval for which the torque was exerted. The units for angular momentum are kilogram meters squared per second or kgm^2/s.
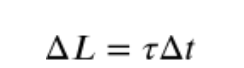
It is also important to note that the net angular momentum of a system is the vector sum of the angular momentum of each object in the system. This is because angular momentum is a vector quantity and follows the rules of vector addition. The total angular momentum of the system is the sum of all the individual angular momenta of the objects in the system, and the direction of the total angular momentum is determined by the directions of the individual angular momenta.
EXAMPLE: (AP Classroom)

The left end of a rod of length d and rotational inertia I is attached to a frictionless horizontal surface by a frictionless pivot, as shown above. Point C marks the center (midpoint) of the rod. The rod is initially motionless but is free to rotate around the pivot.
A student will slide a disk of mass:

toward the rod with velocity v0 perpendicular to the rod, and the disk will stick to the rod a distance x from the pivot.
The student wants the rod-disk system to end up with as much angular speed as possible.

Briefly explain your reasoning without manipulating equations.
CORRECT ANSWER: To the right of C
REASONING: To make the largest angular speed, the rod needs to get the greatest angular momentum possible (L=I𝜔). To get the largest angular momentum, the rod must be given the greatest possible torque. Since torque depends on the moment of inertia and the angular acceleration (𝜏=Iα), and the moment of inertia is calculated using I=cMR^2 (where c is a constant depending on the object), hitting the rod at the greatest radius will produce the greatest torque. Because the pivot is on the left side of C, we want to hit on the right side of C to maximize the radius so the moment of inertia increases, causing the net torque to increase, which will increase the angular speed.
ALTERNATE EXPLANATION: To create the largest angular speed, the rod needs to get the greatest angular momentum possible (L=I𝜔). To do this, we want the disk to transfer the greatest amount of momentum to the rod. Since angular momentum is conserved in the rod-disk system (no outside torques), this means that we want the initial angular momentum of the disk to be as large as possible. The angular momentum of the disk is equal to L=mvr where r is the distance from the pivot because the disk is moving in a straight-line motion relative to the pivot point of the rod.
To make:
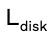
the largest it can possibly be, it needs to hit at the greatest distance away from the pivot to maximize the value of r. The greatest distance away from the pivot is on the right side of C.
(This explanation uses the law of conservation of momentum which will be covered in the next section.)
🎥Watch: AP Physics 1 - Unit 7 Streams
Practice Problems
1. A spinning disk has a mass of 0.5 kg and a radius of 0.2 m. The disk is spinning at an angular velocity of 2 rad/s. What is the angular momentum of the disk? (I = 1/2MR^2 for the disk)
A) 0.02 kgm^2/s B) 0.2 kgm^2/s C) 0.4 kgm^2/s D) 0.8 kgm^2/s
The solution is: L = Iω = (1/2) mr^2ω = (1/2)*0.5(*0.2^2)2 = 0.02 kgm^2/s
The answer is A) 0.02 kgm^2/s
2. A 0.4 kg ball is attached to a string of length 0.5 m and is rotating in a circle with an angular velocity of 3 rad/s. What is the angular momentum of the ball? (I= 2/5MR^2 for the ball)
A) 0.3 kgm^2/s B) 0.12 kgm^2/s C) 0.9 kgm^2/s D) 1.2 kgm^2/s
The solution is:
L = Iω = (2/5) mr^2ω = (2/5)*0.4(*0.5^2)3 = 0.12 kgm^2/s The answer is:
A) 0.12 kgm^2/s
3. A flywheel (disk) with a mass of 8 kg and a radius of 0.3 m is spinning at an angular velocity of 4 rad/s. What is the angular momentum of the flywheel? (I = 1/2MR^2 for the flywheel)
A) 1.44 kgm^2/s B) 2.4 kgm^2/s C) 4.8 kgm^2/s D) 9.6 kgm^2/s
The solution is:
L = Iω = (1/2) mr^2ω = (1/2)*8(*0.3^2)4 = 1.44 kgm^2/s The answer is
A) 1.44 kgm^2/s

© 2024 Fiveable Inc. All rights reserved.