Browse By Unit
10.3 Interference and Superposition (Waves in Tubes and on Strings)
7 min read•june 18, 2024
Peter Apps
Peter Apps
As of 2021, College Board only tests Units 1-7 on the AP Physics 1 exam. This page's content will not be tested on the exam, but we kept it online for you all as a resource.
Enduring Understanding 6.D 👨💻
Interference and superposition lead to standing waves and beats.
Essential Knowledge 6.D.1 🏘
Two or more wave pulses can interact in such a way as to produce amplitude variations in the resultant wave. When two pulses cross, they travel through each other; they do not bounce off each other. Where the pulses overlap, the resulting displacement can be determined by adding the displacements of the two pulses. This is called superposition.
Essential Knowledge 6.D.2 🏘
Two or more traveling waves can interact in such a way as to produce amplitude variations in the resultant wave.
Essential Knowledge 6.D.3 🏘
Standing waves are the result of the addition of incident and reflected waves that are confined to a region and have nodes and antinodes. Examples include waves on a fixed length of string and sound waves in both closed and open tubes.
Essential Knowledge 6.D.4 🏘
The possible wavelengths of a standing wave are determined by the size of the region to which it is confined.
Essential Knowledge 6.D.5 🏘
Beats arise from the addition of waves of slightly different frequency.
This section focuses on what happens when two waves overlap. There are two main situations that this occurs in that the AP focuses on: A wave in a string or A wave in a tube. Both of these situations are commonly seen in musical instruments such as organs, pianos, guitars, and wind instruments.
Superposition & Interference Patterns
A superposition occurs when two (or more) waves overlap. This changes the amplitude of the wave as long as the waves are overlapping. Once the waves have passed through each other, they return to their original amplitudes. To determine the amplitude of the overlapping waves, simply add the amplitudes together at every point. In the image below, notice how the amplitude of the waves increases when the waves overlap, but then returns to their original values after the waves have passed through each other.

Image courtesy of CyberPhysics.
Beats
Beats occur when two waves which are almost identical to each other interfere. This leads to a large variation in the observed amplitude that repeats in a regular pattern. The frequency of the beats is equal to the difference in the frequencies of the individual waves. The lower the beat frequency, the closer the two waves are to having the same frequency. This feature is often used to tune musical instruments by ear. The image below gives a visual representation of how beats occur.

Image courtesy of Pellissippi State Community College.
When the crests and troughs of f1 and f2 are in phase, they are really close to matching up and produce a wave with greater amplitude (constructive interference). A short time later though, differences in the frequencies have moved the waves out of phase, resulting in destructive interference and a smaller amplitude of the superposition.
Standing Waves
Standing Waves are formed when two waves with the same amplitude, wavelength, and frequency interfere with each other. This creates a wave that appears to “stand still” even though the waves are still propagating through it. Standing waves are also created through constructive and destructive interference. The areas of maximum constructive interference are referred to as Antinodes, while the areas of maximum destructive interference are referred to as Nodes. (A trick to remember - Nodes have No motion)
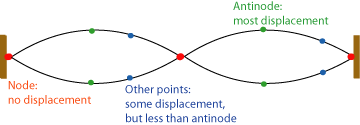
Image courtesy of Open Curriculum.
The simplest standing wave is called the fundamental. It contains 1 antinode and 2 nodes. By increasing the frequency of the wave, different standing waves can be created. These are collectively referred to as Harmonics. The chart below shows a variety of different harmonics. Notice that the total length (L) of the string remains constant and that we can use that to determine the wavelength of the wave.
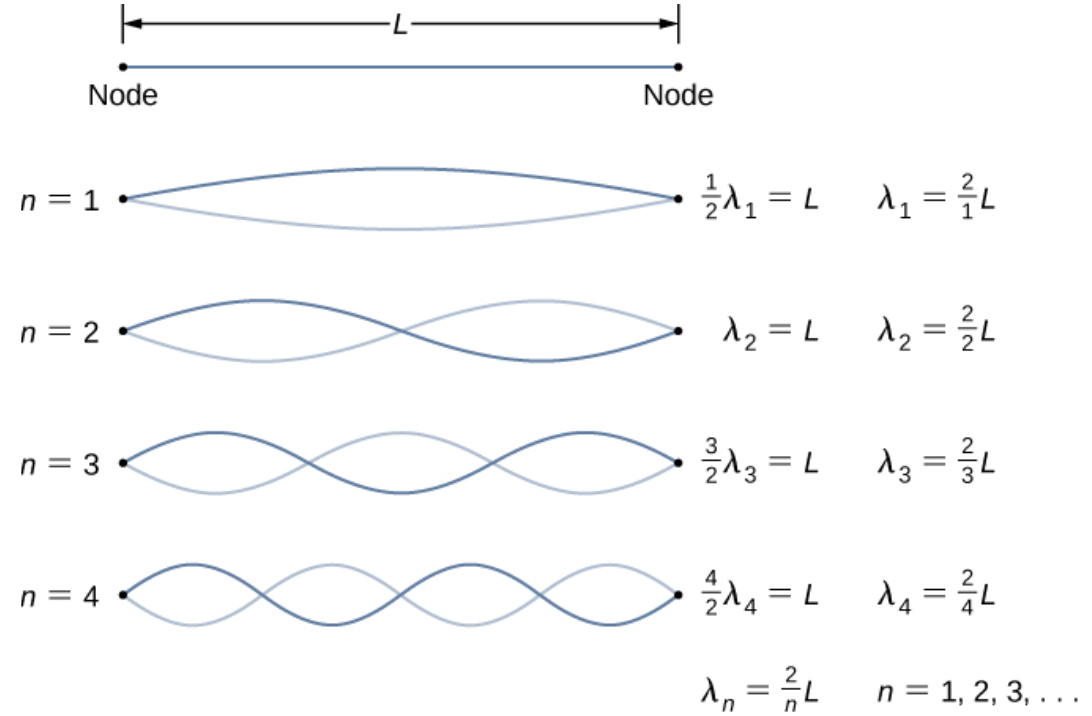
Image courtesy of OpenStax.
Open and Closed Tubes
Standing waves can also form inside tubes. This is the physical basis for many musical instruments. By changing the length of the tube or the frequency of the vibrations different notes can be created. There are 2 types of tubes we need to be familiar with: Tubes that are open on both ends (Open-Open) and Tubes that are closed on one end (Open-Closed). For both of these tubes, they will produce a note (or resonate) when an antinode is present at the all of the open ends of the tube.
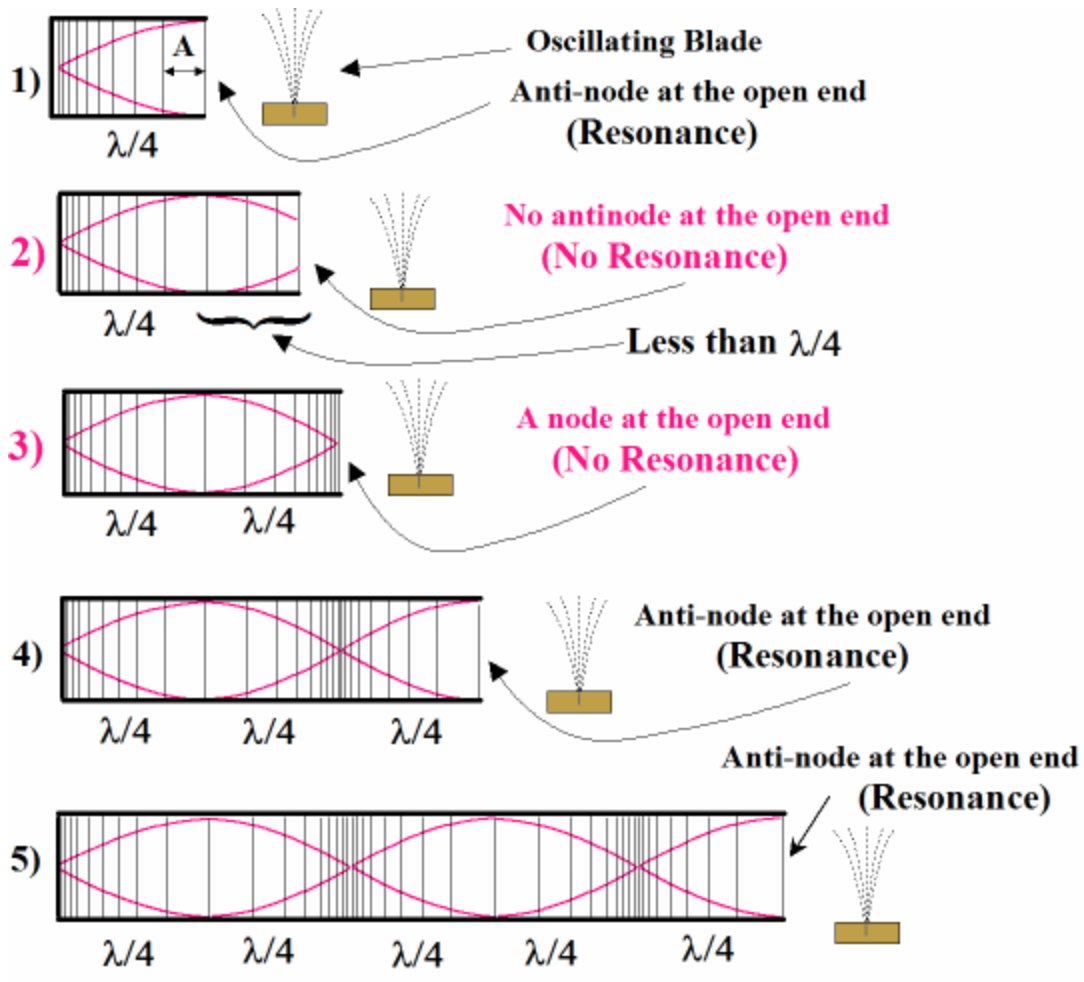
Image courtesy of TGHS Level 3 Physics.
In Cases 2 and 3, the length of the pipe is such that antinode does not happen at the open end of th pipe that means "No Resonance". In each of cases 1, 4 and 5, the pipelength is an odd-multiple of:
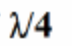
for which "Resonance" occurs.
Since resonance only occurs when an antinode is present at the open end of the tube, a Open-Closed pipe will resonate anytime there isn’t a whole or half wave in the tube. Compare this with an Open-Open pipe in the table below that will resonate at every harmonic.
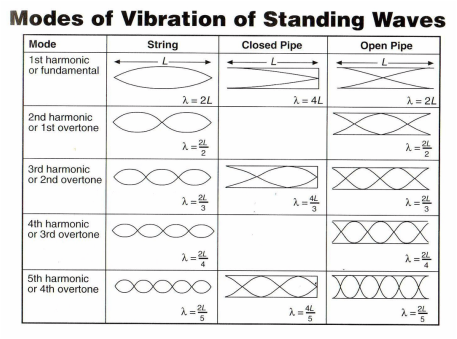
Image courtesy of TGHS Level 3 Physics.
Sample Question (AP Classroom)
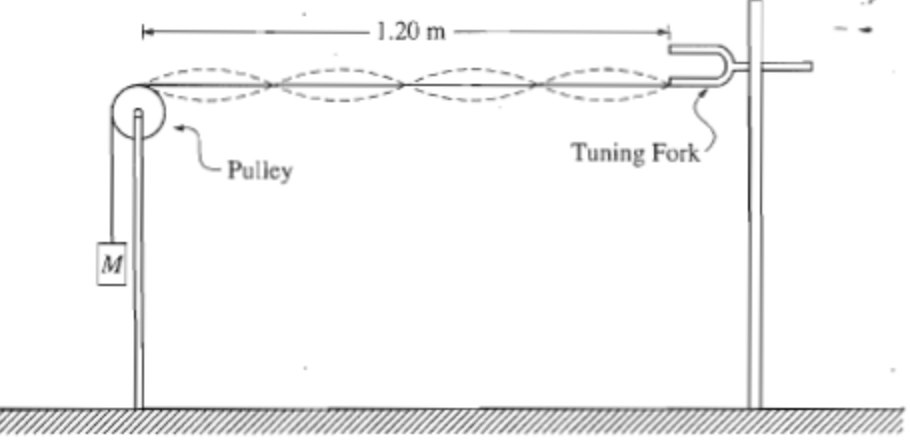
To demonstrate standing waves, one end of a string is attached to a tuning fork with frequency 120 Hz. The other end of the string passes over a pulley and is connected to a suspended mass M as shown in the figure above. The value of M is such that the standing wave pattern has four "loops." The length of the string from the tuning fork to the point where the string touches the top of the pulley is 1.20 m. The linear density of the string is 1.0 x 10^-4 kg/m, and remains constant throughout the experiment.
(a) Determine the wavelength of the standing wave.
(b) Determine the speed of transverse waves along the string.
(c) The speed of waves along the string increases with increasing tension in the string. Indicate whether the value of M should be increased or decreased in order to double the number of loops in the standing wave pattern. Justify your answer.
(d) If a point on the string at an antinode moves a total vertical distance of 4 cm during one complete cycle, what is the amplitude of the standing wave?
Answer:
(a) The diagram shows 2 complete waves in 1.2m so the wavelength will be 0.6m.
(b) We’re told the frequency of the vibrations is 120Hz.
(c) Doubling the number of loops, means the wavelength will have to decrease. Since the frequency is constant, decreasing the wavelength will result in the speed of the wave decreasing. To do this the tension on the string must be lowered, so the value of M will have to be decreased.
(d) An antinode in a full cycle of the wave moves from a crest to a trough and back to a crest again (moving 4x the amplitude of the wave). Therefore the amplitude of this wave must be 1cm.
Sample Question (2019 AP Exam)
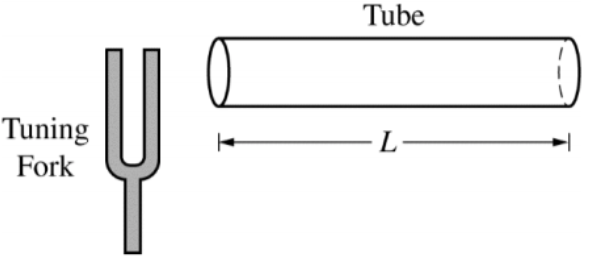
A tuning fork vibrating at 512 Hz is held near one end of a tube of length L that is open at both ends, as shown above. The column of air in the tube resonates at its fundamental frequency. The speed of sound in air is 340 m/s.
(a) Calculate the length L of the tube. (b) The column of air in the tube is still resonating at its fundamental frequency. On the axes below, sketch a graph of the maximum speed of air molecules as they oscillate in the tube, as a function of position x, from x = 0 (left end of tube) to x = L (right end of tube). (Ignore random thermal motion of the air molecules.)
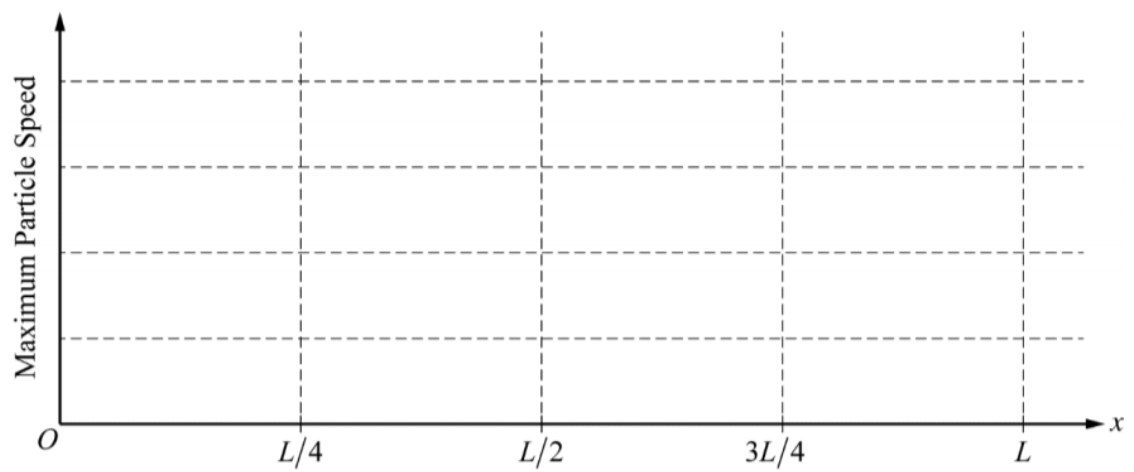
(c) The right end of the tube is now capped shut, and the tube is placed in a chamber that is filled with another gas in which the speed of sound is 1005 m s. Calculate the new fundamental frequency of the tube.
Answers:
(a) The tube is vibrating at its fundamental frequency, this means that there must be an antinode at both ends of the tube and the wave must be as simple as possible. For the open-open tube, this means that ½ of a wave fits in the tube, so the wavelength is twice L. Since we’re given v and f we can find the wavelength, then divide it in half to get L.
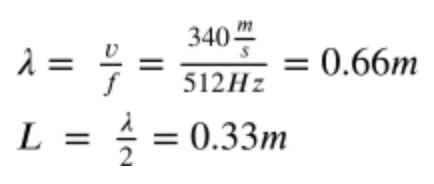
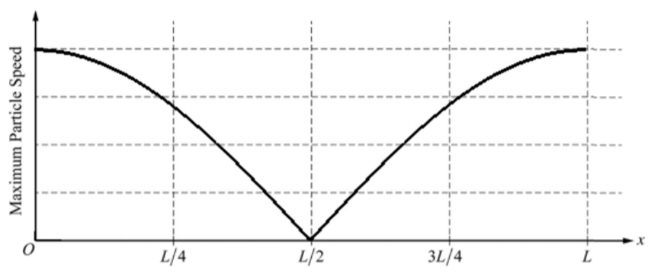
(b) Since there are antinodes at each end of the tube, there must be a node centered in the tube (L/2). Antinodes have maximum velocity, and nodes have 0 velocity.
(c) This is similar to part a, except the tube is now Open-Closed. The fundamental now has ¼ of the wave inside the tube so the L=4λ.

🎥Watch: AP Physics 1 - Unit 10 Streams
<< Hide Menu
10.3 Interference and Superposition (Waves in Tubes and on Strings)
7 min read•june 18, 2024
Peter Apps
Peter Apps
As of 2021, College Board only tests Units 1-7 on the AP Physics 1 exam. This page's content will not be tested on the exam, but we kept it online for you all as a resource.
Enduring Understanding 6.D 👨💻
Interference and superposition lead to standing waves and beats.
Essential Knowledge 6.D.1 🏘
Two or more wave pulses can interact in such a way as to produce amplitude variations in the resultant wave. When two pulses cross, they travel through each other; they do not bounce off each other. Where the pulses overlap, the resulting displacement can be determined by adding the displacements of the two pulses. This is called superposition.
Essential Knowledge 6.D.2 🏘
Two or more traveling waves can interact in such a way as to produce amplitude variations in the resultant wave.
Essential Knowledge 6.D.3 🏘
Standing waves are the result of the addition of incident and reflected waves that are confined to a region and have nodes and antinodes. Examples include waves on a fixed length of string and sound waves in both closed and open tubes.
Essential Knowledge 6.D.4 🏘
The possible wavelengths of a standing wave are determined by the size of the region to which it is confined.
Essential Knowledge 6.D.5 🏘
Beats arise from the addition of waves of slightly different frequency.
This section focuses on what happens when two waves overlap. There are two main situations that this occurs in that the AP focuses on: A wave in a string or A wave in a tube. Both of these situations are commonly seen in musical instruments such as organs, pianos, guitars, and wind instruments.
Superposition & Interference Patterns
A superposition occurs when two (or more) waves overlap. This changes the amplitude of the wave as long as the waves are overlapping. Once the waves have passed through each other, they return to their original amplitudes. To determine the amplitude of the overlapping waves, simply add the amplitudes together at every point. In the image below, notice how the amplitude of the waves increases when the waves overlap, but then returns to their original values after the waves have passed through each other.

Image courtesy of CyberPhysics.
Beats
Beats occur when two waves which are almost identical to each other interfere. This leads to a large variation in the observed amplitude that repeats in a regular pattern. The frequency of the beats is equal to the difference in the frequencies of the individual waves. The lower the beat frequency, the closer the two waves are to having the same frequency. This feature is often used to tune musical instruments by ear. The image below gives a visual representation of how beats occur.

Image courtesy of Pellissippi State Community College.
When the crests and troughs of f1 and f2 are in phase, they are really close to matching up and produce a wave with greater amplitude (constructive interference). A short time later though, differences in the frequencies have moved the waves out of phase, resulting in destructive interference and a smaller amplitude of the superposition.
Standing Waves
Standing Waves are formed when two waves with the same amplitude, wavelength, and frequency interfere with each other. This creates a wave that appears to “stand still” even though the waves are still propagating through it. Standing waves are also created through constructive and destructive interference. The areas of maximum constructive interference are referred to as Antinodes, while the areas of maximum destructive interference are referred to as Nodes. (A trick to remember - Nodes have No motion)

Image courtesy of Open Curriculum.
The simplest standing wave is called the fundamental. It contains 1 antinode and 2 nodes. By increasing the frequency of the wave, different standing waves can be created. These are collectively referred to as Harmonics. The chart below shows a variety of different harmonics. Notice that the total length (L) of the string remains constant and that we can use that to determine the wavelength of the wave.

Image courtesy of OpenStax.
Open and Closed Tubes
Standing waves can also form inside tubes. This is the physical basis for many musical instruments. By changing the length of the tube or the frequency of the vibrations different notes can be created. There are 2 types of tubes we need to be familiar with: Tubes that are open on both ends (Open-Open) and Tubes that are closed on one end (Open-Closed). For both of these tubes, they will produce a note (or resonate) when an antinode is present at the all of the open ends of the tube.

Image courtesy of TGHS Level 3 Physics.
In Cases 2 and 3, the length of the pipe is such that antinode does not happen at the open end of th pipe that means "No Resonance". In each of cases 1, 4 and 5, the pipelength is an odd-multiple of:
for which "Resonance" occurs.
Since resonance only occurs when an antinode is present at the open end of the tube, a Open-Closed pipe will resonate anytime there isn’t a whole or half wave in the tube. Compare this with an Open-Open pipe in the table below that will resonate at every harmonic.

Image courtesy of TGHS Level 3 Physics.
Sample Question (AP Classroom)

To demonstrate standing waves, one end of a string is attached to a tuning fork with frequency 120 Hz. The other end of the string passes over a pulley and is connected to a suspended mass M as shown in the figure above. The value of M is such that the standing wave pattern has four "loops." The length of the string from the tuning fork to the point where the string touches the top of the pulley is 1.20 m. The linear density of the string is 1.0 x 10^-4 kg/m, and remains constant throughout the experiment.
(a) Determine the wavelength of the standing wave.
(b) Determine the speed of transverse waves along the string.
(c) The speed of waves along the string increases with increasing tension in the string. Indicate whether the value of M should be increased or decreased in order to double the number of loops in the standing wave pattern. Justify your answer.
(d) If a point on the string at an antinode moves a total vertical distance of 4 cm during one complete cycle, what is the amplitude of the standing wave?
Answer:
(a) The diagram shows 2 complete waves in 1.2m so the wavelength will be 0.6m.
(b) We’re told the frequency of the vibrations is 120Hz.
(c) Doubling the number of loops, means the wavelength will have to decrease. Since the frequency is constant, decreasing the wavelength will result in the speed of the wave decreasing. To do this the tension on the string must be lowered, so the value of M will have to be decreased.
(d) An antinode in a full cycle of the wave moves from a crest to a trough and back to a crest again (moving 4x the amplitude of the wave). Therefore the amplitude of this wave must be 1cm.
Sample Question (2019 AP Exam)

A tuning fork vibrating at 512 Hz is held near one end of a tube of length L that is open at both ends, as shown above. The column of air in the tube resonates at its fundamental frequency. The speed of sound in air is 340 m/s.
(a) Calculate the length L of the tube. (b) The column of air in the tube is still resonating at its fundamental frequency. On the axes below, sketch a graph of the maximum speed of air molecules as they oscillate in the tube, as a function of position x, from x = 0 (left end of tube) to x = L (right end of tube). (Ignore random thermal motion of the air molecules.)

(c) The right end of the tube is now capped shut, and the tube is placed in a chamber that is filled with another gas in which the speed of sound is 1005 m s. Calculate the new fundamental frequency of the tube.
Answers:
(a) The tube is vibrating at its fundamental frequency, this means that there must be an antinode at both ends of the tube and the wave must be as simple as possible. For the open-open tube, this means that ½ of a wave fits in the tube, so the wavelength is twice L. Since we’re given v and f we can find the wavelength, then divide it in half to get L.
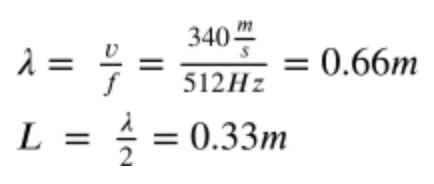
(b) Since there are antinodes at each end of the tube, there must be a node centered in the tube (L/2). Antinodes have maximum velocity, and nodes have 0 velocity.

(c) This is similar to part a, except the tube is now Open-Closed. The fundamental now has ¼ of the wave inside the tube so the L=4λ.

🎥Watch: AP Physics 1 - Unit 10 Streams

© 2024 Fiveable Inc. All rights reserved.