Browse By Unit
Kinematic Equations and Derivations
6 min read•july 11, 2024
QiLin Xue
QiLin Xue
In AP Physics, the first thing you learn is typically kinematics - that is the physics of motion. Whether 1 dimensional or 2 dimensional, the kinematic equations (Sometimes called SUVAT equations) are key tools in finding displacement, initial or final velocities, and other quantities like acceleration and time. So, what are the kinematic equations and how do you derive them?
Choosing a Kinematic Equation
When an object moves from A to point B under a constant acceleration, there are five quantities that describe the motion:
- The displacement (Δd)
- Initial Velocity (vᵢ)
- Final Velocity (v)
- Acceleration (a)
- Time taken (t)
Fun Fact: you only need to know just three of these quantities in order to determine the other two! College Board gives the following equations on the equation sheet:
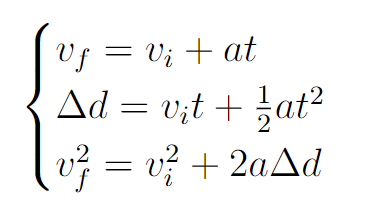
Note that College Board drops the subscript for final position and velocity but feel free to leave them on to avoid misunderstandings.
You should also know the following definition of average velocity. Occasionally you will need this:
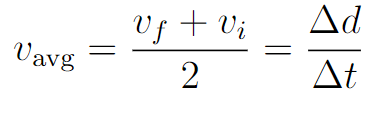
Steps To Solve A Problem
(1) List all the variables you know and their values. Remember, you just need at least three! Here’s a few tips if it’s not explicitly stated.
- During free fall, the magnitude of the vertical acceleration is g = 9.8m/s²
- If the starting and final position is equal, you may set Δd to zero
- At the top of a trajectory, the vertical component of the velocity will be zero.
- If needed, draw a picture! Pictures can help you label values and get a better perspective as to how things work kinematically
(2) Determine the variable you are solving for
and
(3) Determine the relevant equation(s) to use.
- Oftentimes there is a “missing quantity” that is not given, and you do not need to solve for it. Note that each equation excludes exactly one variable. Picking the equation that does not include this “missing quantity” is the best way to proceed.
(4) Plug the values in and solve
Example
Romeo throws a bouquet of flowers up a building. What is the minimum speed he needs to throw the flowers such that it lands in Juliet's balcony, which is at a height of 5 meters above him?
First, we will determine as many known variables as possible. At first, this may seem troubling as there is only one number in the question! We only know that the vertical displacement Δd is 5 meters.
However, because the object travels through the air it experiences a constant acceleration of -9.8 m/s².
Finally, we will use the last piece of information we haven't used yet: we wish to find the minimum speed. In other words, Romeo needs to throw the flowers up in such a way where it reaches the balcony but just barely. This occurs when the balcony is at the top of the trajectory or when the velocity is zero.
Here we found our three quantities:
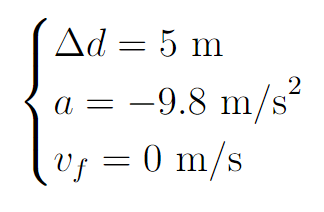
The quantity we wish to find is the initial velocity. The only equation that includes only these four variables in equation 3:
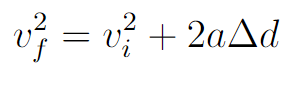
Solving for initial velocity gives:

Remarks: Notice that the equation we chose did not depend on time. Whenever you don't get the value of the time elapsed, this equation is almost always the right way to go.
Deriving the Equations
A traditional physics course would formally derive the kinematic equations with calculus. However, there is a far more intuitive and beautiful way of looking at them with just plain algebra.
Deriving v = vᵢ + at
First, we will plot velocity vs time on a graph.

This graph represents an object that starts with an initial velocity and steadily increases it as time grows.
The slope of the graph is Δv/Δt which is the definition of acceleration. The y-intercept is the velocity of the object at t=0 or the initial velocity vᵢ. Using y=mx+b, the general form of the line is:
y = ax + vᵢ
The x-axis is time and the y-axis is velocity so substituting those variables give:
v = at + vᵢ
Remarks: this could have also been derived using the definition of acceleration a = (v-vᵢ)/t and then rearranging to solve for v. However I chose this slightly different way to create the basis for the next section.
Deriving Δd = vᵢt + 1/2 at^2
Before we move on to this derivation, we will first show that the area under the velocity vs time graph is the displacement. If you are already familiar, you may skip the next subsection.
Area of v-t graph is displacement
If you jog at 2 m/s for 4 seconds, it is not hard to see that your displacement will be 8 meters. Graphically, this is represented by the area traveled: vt=Δd.
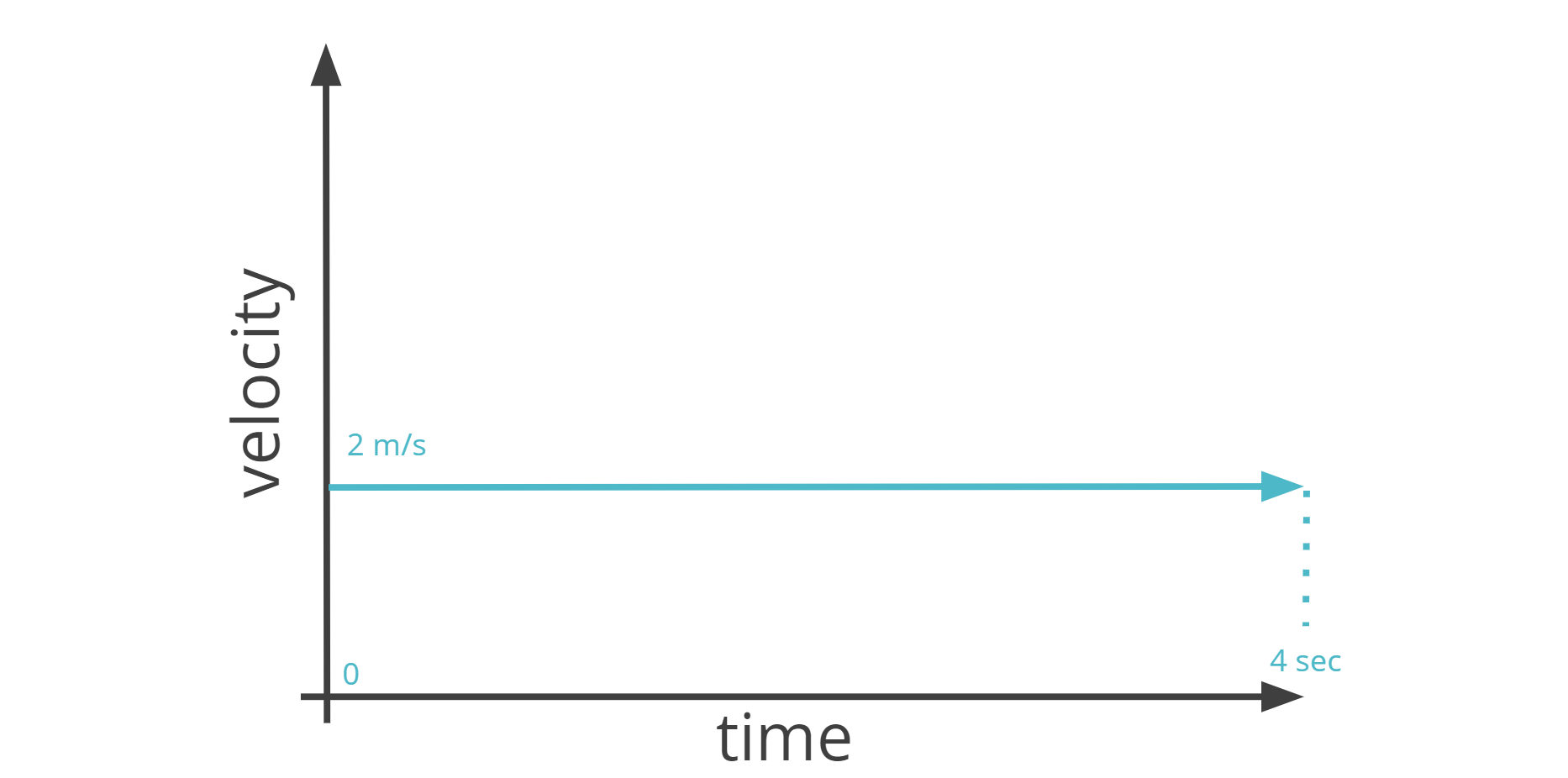
Now suppose there is a sudden jump in your journey. You jog at 2 m/s for the first 2 seconds but for the last 2 seconds you suddenly sprint at a speed of 4 m/s. We can determine the displacement by breaking the journey up into two sections, finding the displacement for each, and adding both up. This is equivalent to finding the area under the graph.
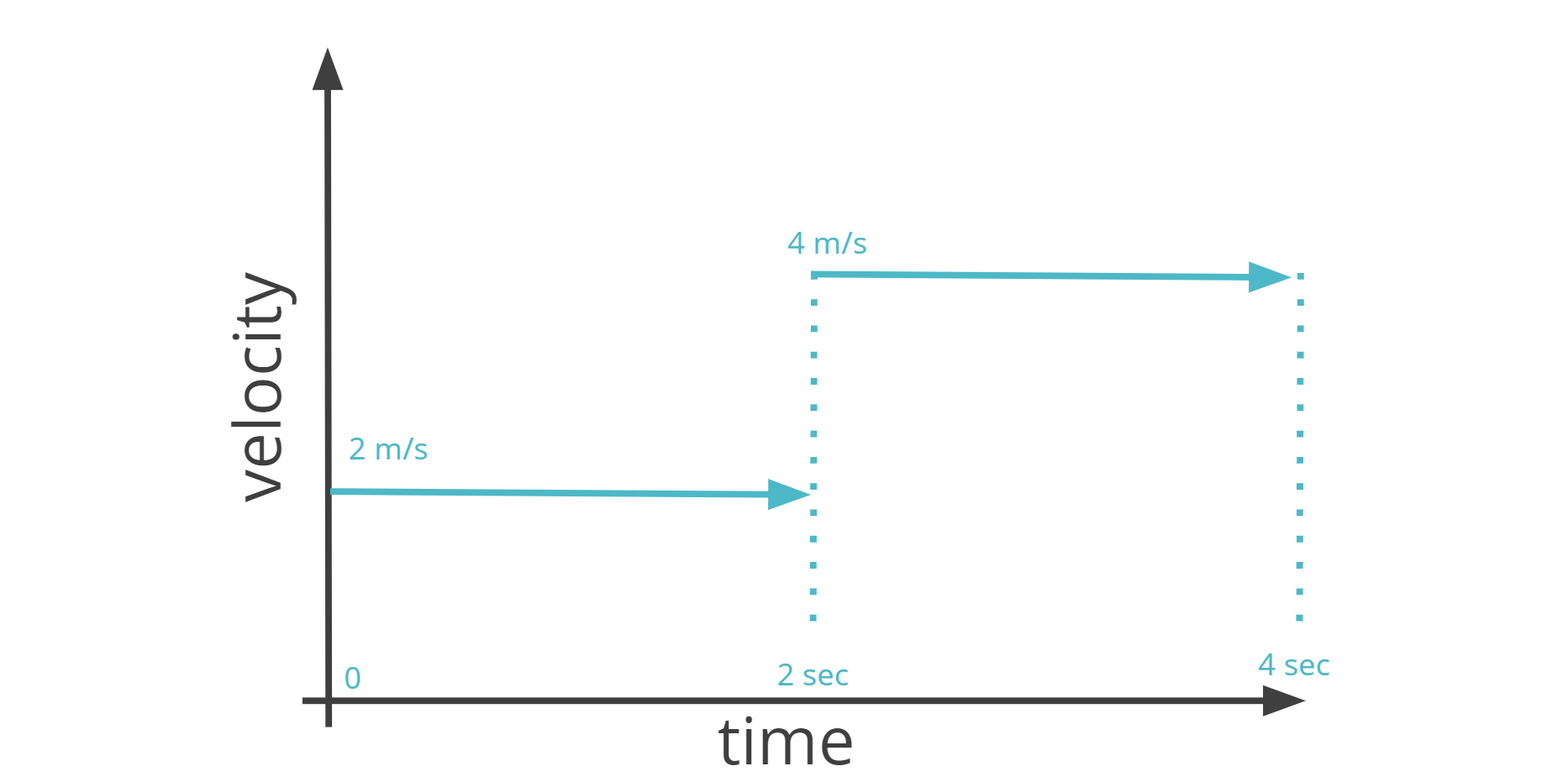
Now suppose you change speeds 100 times during the journey each time slightly faster than before. We can find the area of the graph by breaking it up into 100 small rectangles or we can approximate it as a triangle. The more times you change speeds, the more accurate it will be. Under a constant acceleration, you will be constantly changing speeds and therefore the "approximation" will be exact. If you find the area under the graph, you can find the displacement.

Remarks: Someone who has learned calculus before would have recognized this as a Riemann Sum. If you don't know calculus, I just tricked you into reading a brief introduction to it. But don't worry, this is the hardest part to understand.
Finding the area of the v-t graph
Refer to the velocity-time graph earlier. What is the area?
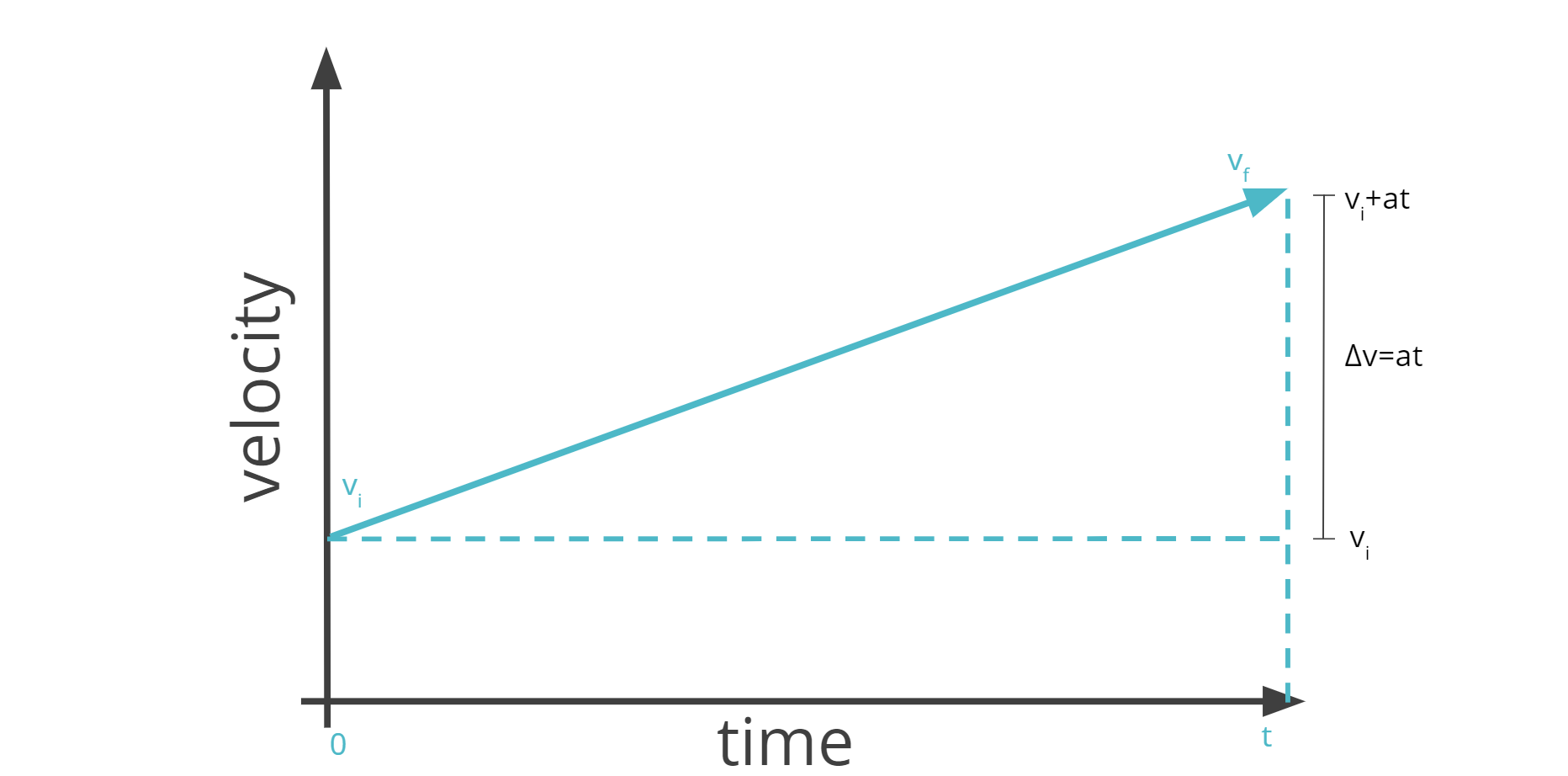
We can break the "trapezoid" into two parts: the rectangle at the bottom and the triangle at the top.
The area of the rectangle is given by vᵢt
The area of the triangle is given by 1/2 bh = 1/2 (t)(Δv) = 1/2 (t)(at) = 1/2 at^2
Adding the two areas together gives A = vᵢt + 1/2 at^2 which gives the equation for displacement!
Deriving v^2 = vᵢ^2 + 2aΔd
Fortunately (or unfortunately), this equation is derived in the same way as the last equation just with a bit of algebraic manipulation. We again find the area of the velocity-time graph, but we change our variables around a bit.
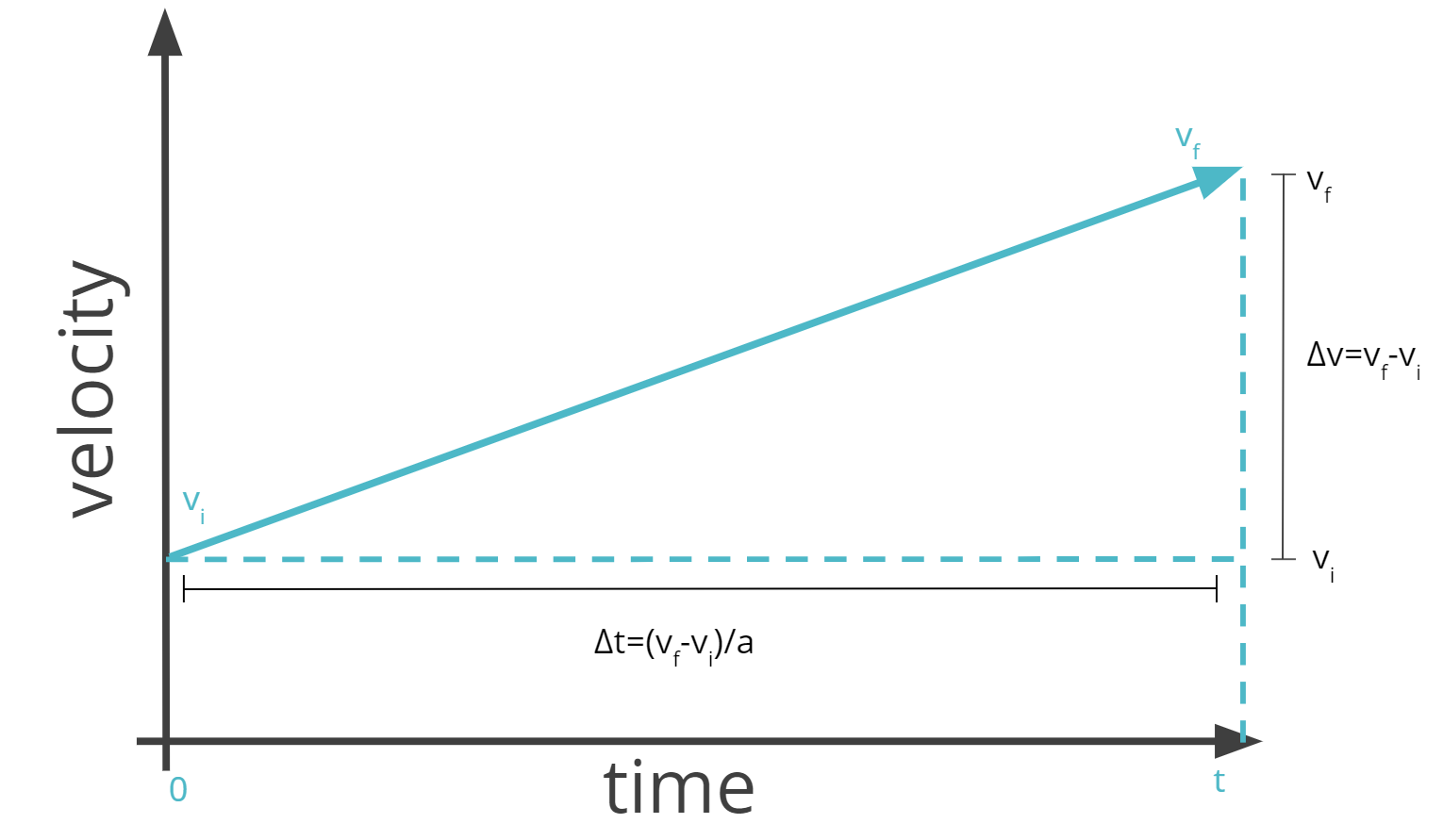
The height of the triangle is now the final velocity minus the initial velocity. The base is now Δt = (v - vᵢ)/a. This last part comes from the definition of acceleration: a = (v-vᵢ)/Δt and rearranging to solve for Δt.
Now, summing up the area of the triangle gives:
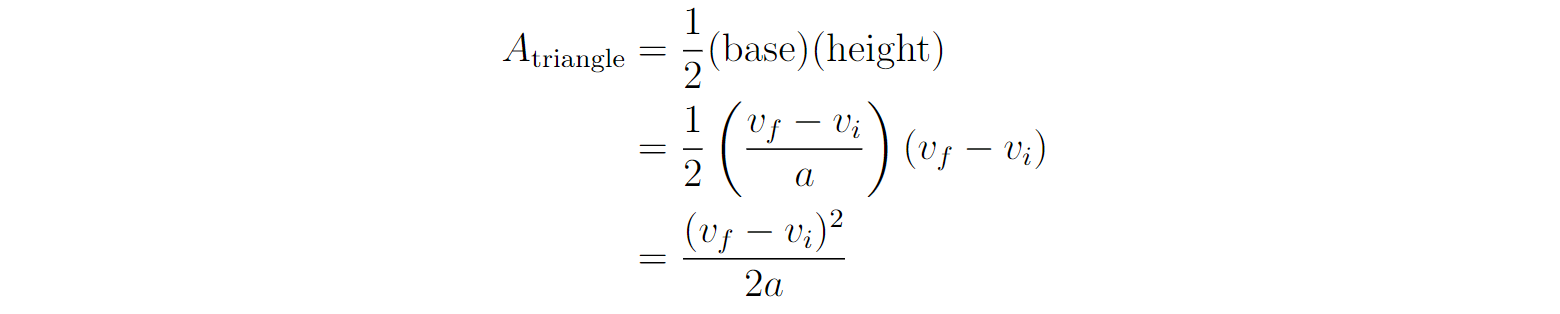
The area of the rectangle is:
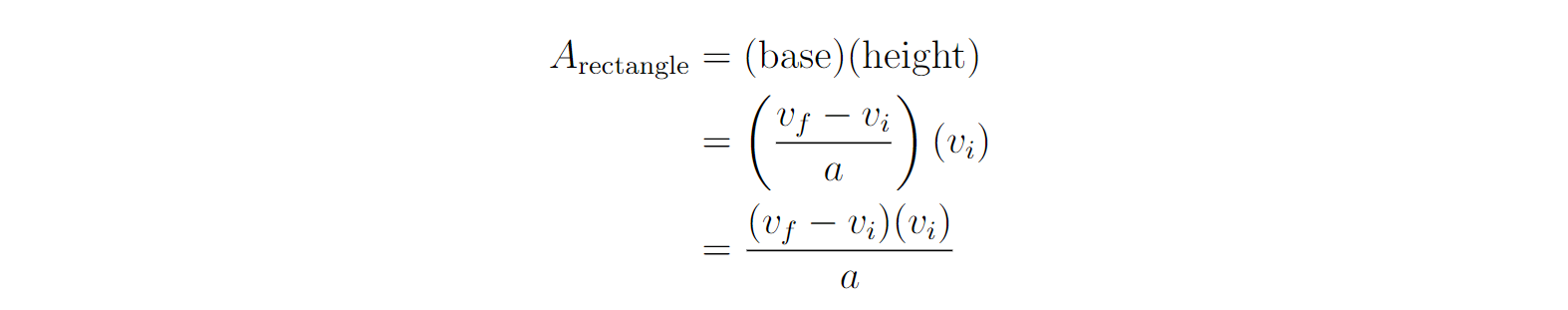
Altogether the area (displacement) can be expressed by and via some algebraic manipulation:
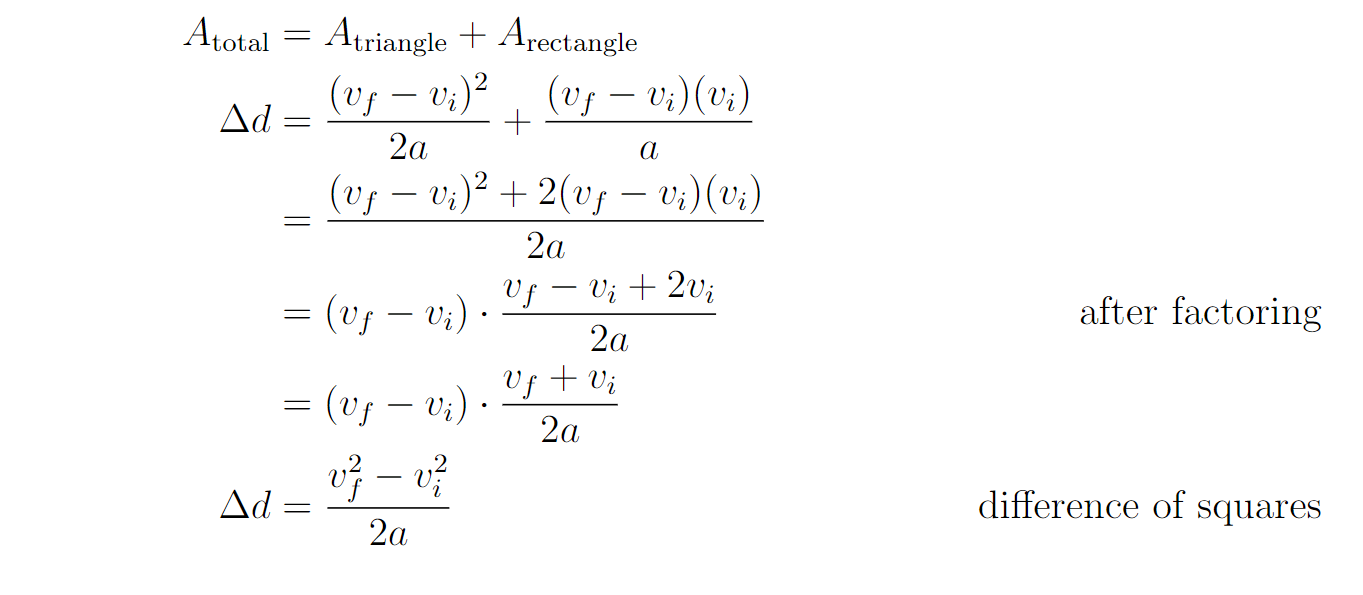
And rearranging the last part finally gives:

This last derivation doesn't have any nice intuitive way of looking at it. Someone with a keen eye may ask: velocity is a vector, so is velocity squared still a vector? Is it even legal to multiply two vectors together like this?
The answer is yes, and it is called a dot product. This will not be the focus of this article but a dot product takes two vectors as input and outputs a scalar.
This draws a lot of connections with the conservation of energy! Both conservation of energy and this equation is time-independent (the Δt term does not appear) and both deal with scalars! (since energy is a scalar)
Perhaps this could lead to a second method of deriving this equation. Think and ponder!
A Note About Acceleration
Please note that the kinematic equations only apply when acceleration is CONSTANT! If acceleration is not constant, you must use calculus to solve for these values. For students in AP Physics 1 or 2, you don't need to worry about this, as your courses are algebra-based. However, if you are in AP Physics C: Mechanics or AP Physics C: Electricity and Magnetism, you will see calculus on your exam (However E&M will not see much, if any kinematics on their exam, mechanics will!).
<< Hide Menu
Kinematic Equations and Derivations
6 min read•july 11, 2024
QiLin Xue
QiLin Xue
In AP Physics, the first thing you learn is typically kinematics - that is the physics of motion. Whether 1 dimensional or 2 dimensional, the kinematic equations (Sometimes called SUVAT equations) are key tools in finding displacement, initial or final velocities, and other quantities like acceleration and time. So, what are the kinematic equations and how do you derive them?
Choosing a Kinematic Equation
When an object moves from A to point B under a constant acceleration, there are five quantities that describe the motion:
- The displacement (Δd)
- Initial Velocity (vᵢ)
- Final Velocity (v)
- Acceleration (a)
- Time taken (t)
Fun Fact: you only need to know just three of these quantities in order to determine the other two! College Board gives the following equations on the equation sheet:
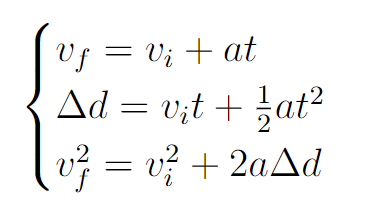
Note that College Board drops the subscript for final position and velocity but feel free to leave them on to avoid misunderstandings.
You should also know the following definition of average velocity. Occasionally you will need this:
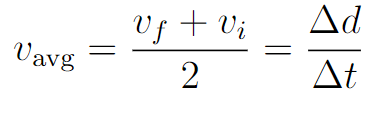
Steps To Solve A Problem
(1) List all the variables you know and their values. Remember, you just need at least three! Here’s a few tips if it’s not explicitly stated.
- During free fall, the magnitude of the vertical acceleration is g = 9.8m/s²
- If the starting and final position is equal, you may set Δd to zero
- At the top of a trajectory, the vertical component of the velocity will be zero.
- If needed, draw a picture! Pictures can help you label values and get a better perspective as to how things work kinematically
(2) Determine the variable you are solving for
and
(3) Determine the relevant equation(s) to use.
- Oftentimes there is a “missing quantity” that is not given, and you do not need to solve for it. Note that each equation excludes exactly one variable. Picking the equation that does not include this “missing quantity” is the best way to proceed.
(4) Plug the values in and solve
Example
Romeo throws a bouquet of flowers up a building. What is the minimum speed he needs to throw the flowers such that it lands in Juliet's balcony, which is at a height of 5 meters above him?
First, we will determine as many known variables as possible. At first, this may seem troubling as there is only one number in the question! We only know that the vertical displacement Δd is 5 meters.
However, because the object travels through the air it experiences a constant acceleration of -9.8 m/s².
Finally, we will use the last piece of information we haven't used yet: we wish to find the minimum speed. In other words, Romeo needs to throw the flowers up in such a way where it reaches the balcony but just barely. This occurs when the balcony is at the top of the trajectory or when the velocity is zero.
Here we found our three quantities:
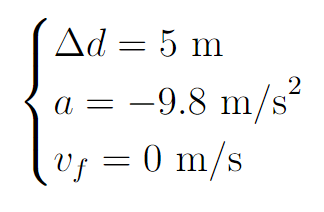
The quantity we wish to find is the initial velocity. The only equation that includes only these four variables in equation 3:
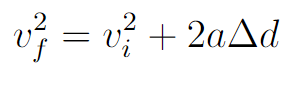
Solving for initial velocity gives:

Remarks: Notice that the equation we chose did not depend on time. Whenever you don't get the value of the time elapsed, this equation is almost always the right way to go.
Deriving the Equations
A traditional physics course would formally derive the kinematic equations with calculus. However, there is a far more intuitive and beautiful way of looking at them with just plain algebra.
Deriving v = vᵢ + at
First, we will plot velocity vs time on a graph.

This graph represents an object that starts with an initial velocity and steadily increases it as time grows.
The slope of the graph is Δv/Δt which is the definition of acceleration. The y-intercept is the velocity of the object at t=0 or the initial velocity vᵢ. Using y=mx+b, the general form of the line is:
y = ax + vᵢ
The x-axis is time and the y-axis is velocity so substituting those variables give:
v = at + vᵢ
Remarks: this could have also been derived using the definition of acceleration a = (v-vᵢ)/t and then rearranging to solve for v. However I chose this slightly different way to create the basis for the next section.
Deriving Δd = vᵢt + 1/2 at^2
Before we move on to this derivation, we will first show that the area under the velocity vs time graph is the displacement. If you are already familiar, you may skip the next subsection.
Area of v-t graph is displacement
If you jog at 2 m/s for 4 seconds, it is not hard to see that your displacement will be 8 meters. Graphically, this is represented by the area traveled: vt=Δd.

Now suppose there is a sudden jump in your journey. You jog at 2 m/s for the first 2 seconds but for the last 2 seconds you suddenly sprint at a speed of 4 m/s. We can determine the displacement by breaking the journey up into two sections, finding the displacement for each, and adding both up. This is equivalent to finding the area under the graph.

Now suppose you change speeds 100 times during the journey each time slightly faster than before. We can find the area of the graph by breaking it up into 100 small rectangles or we can approximate it as a triangle. The more times you change speeds, the more accurate it will be. Under a constant acceleration, you will be constantly changing speeds and therefore the "approximation" will be exact. If you find the area under the graph, you can find the displacement.

Remarks: Someone who has learned calculus before would have recognized this as a Riemann Sum. If you don't know calculus, I just tricked you into reading a brief introduction to it. But don't worry, this is the hardest part to understand.
Finding the area of the v-t graph
Refer to the velocity-time graph earlier. What is the area?

We can break the "trapezoid" into two parts: the rectangle at the bottom and the triangle at the top.
The area of the rectangle is given by vᵢt
The area of the triangle is given by 1/2 bh = 1/2 (t)(Δv) = 1/2 (t)(at) = 1/2 at^2
Adding the two areas together gives A = vᵢt + 1/2 at^2 which gives the equation for displacement!
Deriving v^2 = vᵢ^2 + 2aΔd
Fortunately (or unfortunately), this equation is derived in the same way as the last equation just with a bit of algebraic manipulation. We again find the area of the velocity-time graph, but we change our variables around a bit.

The height of the triangle is now the final velocity minus the initial velocity. The base is now Δt = (v - vᵢ)/a. This last part comes from the definition of acceleration: a = (v-vᵢ)/Δt and rearranging to solve for Δt.
Now, summing up the area of the triangle gives:
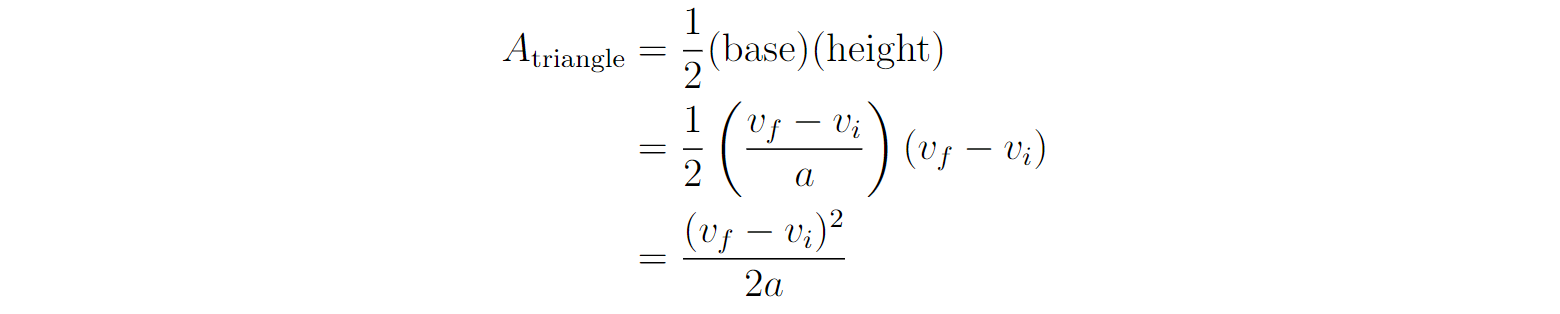
The area of the rectangle is:
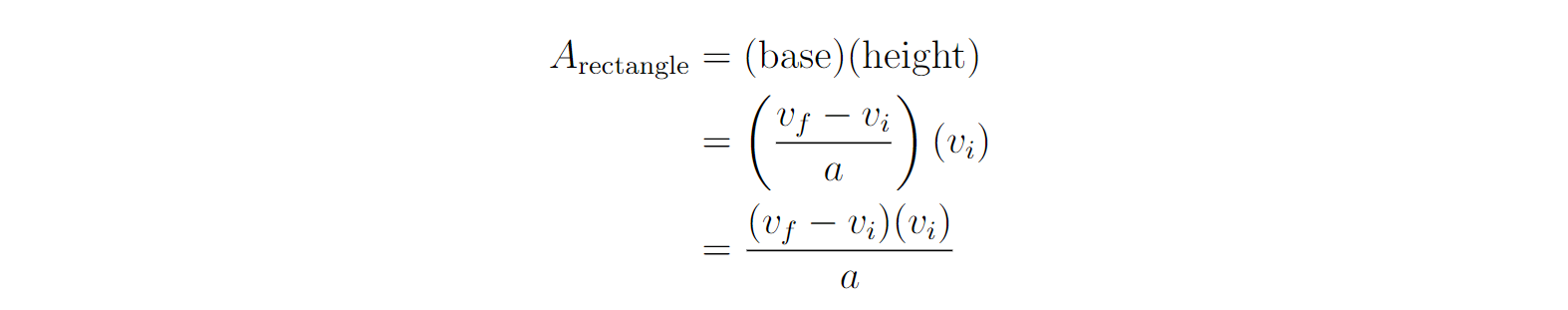
Altogether the area (displacement) can be expressed by and via some algebraic manipulation:
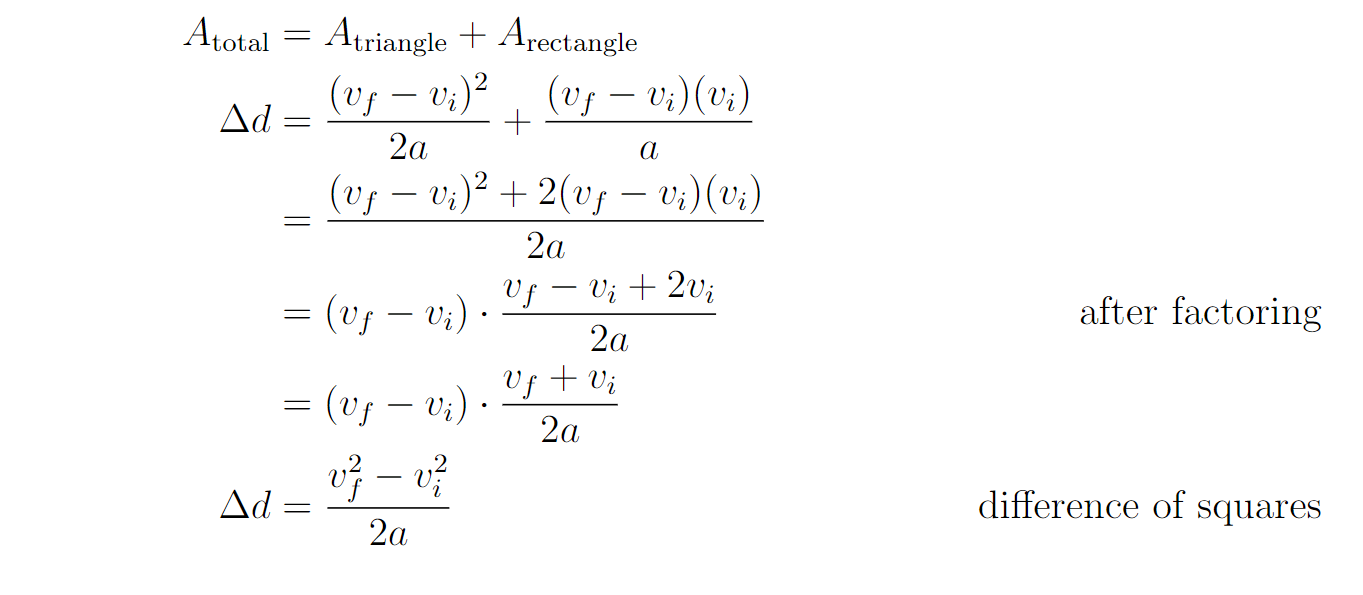
And rearranging the last part finally gives:

This last derivation doesn't have any nice intuitive way of looking at it. Someone with a keen eye may ask: velocity is a vector, so is velocity squared still a vector? Is it even legal to multiply two vectors together like this?
The answer is yes, and it is called a dot product. This will not be the focus of this article but a dot product takes two vectors as input and outputs a scalar.
This draws a lot of connections with the conservation of energy! Both conservation of energy and this equation is time-independent (the Δt term does not appear) and both deal with scalars! (since energy is a scalar)
Perhaps this could lead to a second method of deriving this equation. Think and ponder!
A Note About Acceleration
Please note that the kinematic equations only apply when acceleration is CONSTANT! If acceleration is not constant, you must use calculus to solve for these values. For students in AP Physics 1 or 2, you don't need to worry about this, as your courses are algebra-based. However, if you are in AP Physics C: Mechanics or AP Physics C: Electricity and Magnetism, you will see calculus on your exam (However E&M will not see much, if any kinematics on their exam, mechanics will!).

© 2024 Fiveable Inc. All rights reserved.