Browse By Unit
AP Physics 1 Unit 3 FRQ Practice Prompt & Answers
3 min read•july 11, 2024
Peter Apps
Peter Apps
FRQ practice is one of the most effective ways to prepare for an AP exam! Review these student samples in response to a unit 3 Physics 1 practice prompt, all with corresponding feedback from Fiveable teacher Peter Apps!
Unit 3 FRQ Practice Prompt
An explorer plans a mission to place a satellite into a circular orbit around the planet Jupiter.
a) If the radius of the planned orbit is R, use Newton’s laws to show each of the following.
i. The orbital speed of the planned satellite is given by
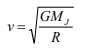
ii. The period of the orbit is given by
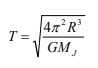
b) The mission goes according to plan and a stable orbit is achieved. However the orbital speed of the satellite is greater than expected. Describe the changes to the orbit, caused by this increase in speed.
FRQ Writing Samples & Feedback
FRQ Writing Submission 1
a) i. FBD of satellite shows that Fg is the net centripetal force on the satellite.
KEY
m1 = mass of Jupiter
m2 = mass of satellite
sumFc = m2ac = m2v^2/R
Gm1/R = v^2
v = sqrt (GM1/R)
ii. Period = time it takes to complete 1 revolution.
tangential velocity x period = circumference of orbit
KEY:
s = orbital circumference
v(T) = s
T = s/v
s = 2piR
v = sqrt(Gm1/R) from part (a)(i)
T = (2piR)/[sqrt(Gm1/R)]
T^2 = 4pi^2R^3/Gm1
T = sqrt(4pi^2R^3/Gm1)
b)
The excess speed will widen the orbital radius because the force of gravity does not provide a strong enough centripetal force at the initial radius:
Gm1m2/R^2 = m2v^2/R
Fg is too small.
Moving farther away decreases v and increases potential energy, and increasing R decreases the required Fg.
Teacher FRQ Feedback
Looks good to me! Part a I)

Part a ii)

Part b)
Since the orbital speed is greater than before, the orbit’s radius is also larger (derivation in part ai). In addition, the larger radius also means that the orbital period is also larger (part aii). Increasing the radius of the orbit also increases the potential energy of the orbit (Ug = - GMm/R) and the kinetic energy of the satellite will be decreased as well (K = 1/2mv^2)
FRQ Writing Submission 2
i. Fnet=ma. Fg=mac. Gmsmj/r^2=mv^2/r. Cancel r, and ms,Gmj/r=v^2/ v=rootGmj/r.
ii. Gmsmj/r^2 = m(2pir/t)^2/r. T^2Gmj=4pi^2r^2r. T= root 4pi^2r^3/GMj. Main point: plug 2pir/T for v.
b. It would decrease the radius as V^2= Gmj/r, G and Mj stay same. With decrease radius, then the period would decrease too
Wouldn't the radius decrease?
Teacher FRQ Feedback
I guess, I needed to be more clear about the question. Assuming the same entry point (distance above the planet), a greater velocity will result in an elliptical orbit, with the closest point of approach being that entry point. Since it’s an ellipse, the farthest point of the orbit will have a larger radius than the circular one, a slower speed at that point (conservation of linear momentum) and more Ug, less KE.
If (as I think you were doing) all we know is that the satellite is moving faster, and assume a circular orbit then yes, you are correct that we’d need a smaller radius which gives more KE and less Ug, and a quicker period.
<< Hide Menu
AP Physics 1 Unit 3 FRQ Practice Prompt & Answers
3 min read•july 11, 2024
Peter Apps
Peter Apps
FRQ practice is one of the most effective ways to prepare for an AP exam! Review these student samples in response to a unit 3 Physics 1 practice prompt, all with corresponding feedback from Fiveable teacher Peter Apps!
Unit 3 FRQ Practice Prompt
An explorer plans a mission to place a satellite into a circular orbit around the planet Jupiter.
a) If the radius of the planned orbit is R, use Newton’s laws to show each of the following.
i. The orbital speed of the planned satellite is given by
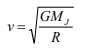
ii. The period of the orbit is given by
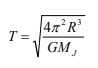
b) The mission goes according to plan and a stable orbit is achieved. However the orbital speed of the satellite is greater than expected. Describe the changes to the orbit, caused by this increase in speed.
FRQ Writing Samples & Feedback
FRQ Writing Submission 1
a) i. FBD of satellite shows that Fg is the net centripetal force on the satellite.
KEY
m1 = mass of Jupiter
m2 = mass of satellite
sumFc = m2ac = m2v^2/R
Gm1/R = v^2
v = sqrt (GM1/R)
ii. Period = time it takes to complete 1 revolution.
tangential velocity x period = circumference of orbit
KEY:
s = orbital circumference
v(T) = s
T = s/v
s = 2piR
v = sqrt(Gm1/R) from part (a)(i)
T = (2piR)/[sqrt(Gm1/R)]
T^2 = 4pi^2R^3/Gm1
T = sqrt(4pi^2R^3/Gm1)
b)
The excess speed will widen the orbital radius because the force of gravity does not provide a strong enough centripetal force at the initial radius:
Gm1m2/R^2 = m2v^2/R
Fg is too small.
Moving farther away decreases v and increases potential energy, and increasing R decreases the required Fg.
Teacher FRQ Feedback
Looks good to me! Part a I)

Part a ii)

Part b)
Since the orbital speed is greater than before, the orbit’s radius is also larger (derivation in part ai). In addition, the larger radius also means that the orbital period is also larger (part aii). Increasing the radius of the orbit also increases the potential energy of the orbit (Ug = - GMm/R) and the kinetic energy of the satellite will be decreased as well (K = 1/2mv^2)
FRQ Writing Submission 2
i. Fnet=ma. Fg=mac. Gmsmj/r^2=mv^2/r. Cancel r, and ms,Gmj/r=v^2/ v=rootGmj/r.
ii. Gmsmj/r^2 = m(2pir/t)^2/r. T^2Gmj=4pi^2r^2r. T= root 4pi^2r^3/GMj. Main point: plug 2pir/T for v.
b. It would decrease the radius as V^2= Gmj/r, G and Mj stay same. With decrease radius, then the period would decrease too
Wouldn't the radius decrease?
Teacher FRQ Feedback
I guess, I needed to be more clear about the question. Assuming the same entry point (distance above the planet), a greater velocity will result in an elliptical orbit, with the closest point of approach being that entry point. Since it’s an ellipse, the farthest point of the orbit will have a larger radius than the circular one, a slower speed at that point (conservation of linear momentum) and more Ug, less KE.
If (as I think you were doing) all we know is that the satellite is moving faster, and assume a circular orbit then yes, you are correct that we’d need a smaller radius which gives more KE and less Ug, and a quicker period.

© 2024 Fiveable Inc. All rights reserved.