Browse By Unit
Avanish Gupta
Milo Chang
Avanish Gupta
Milo Chang
Note: In this topic, we will be using arrayB and the graphical representation of 2D arrays from the previous topic. As a reminder, here is arrayB:
int[][] arrayB = {{1, 2, 3, 4},
{5, 6, 7, 8},
{9, 10, 11, 12}};
General Form
Recall that when traversing a 1D array, you use a loop, usually a for loop or enhanced for loop. This is similar to how we traverse 2D arrays, except in 2D arrays, we need 2 nested for loops, an outer loop traversing through one dimension, and an inner loop traversing through the other. Here is the general form:
for (firstDimension traversal conditions) {
for (secondDimension traversal conditions) {
System.out.print(item + " ");
}
}
System.out.println();
Row-Major vs. Column-Major
There are two main directions we can traverse through. The first is row-major traversal, traversing through every element in one row before moving to the next. Conversely, there is column-major traversal, traversing through every element in one column before moving on to the next.
Row-wise Traversal

Column-wise Traversal
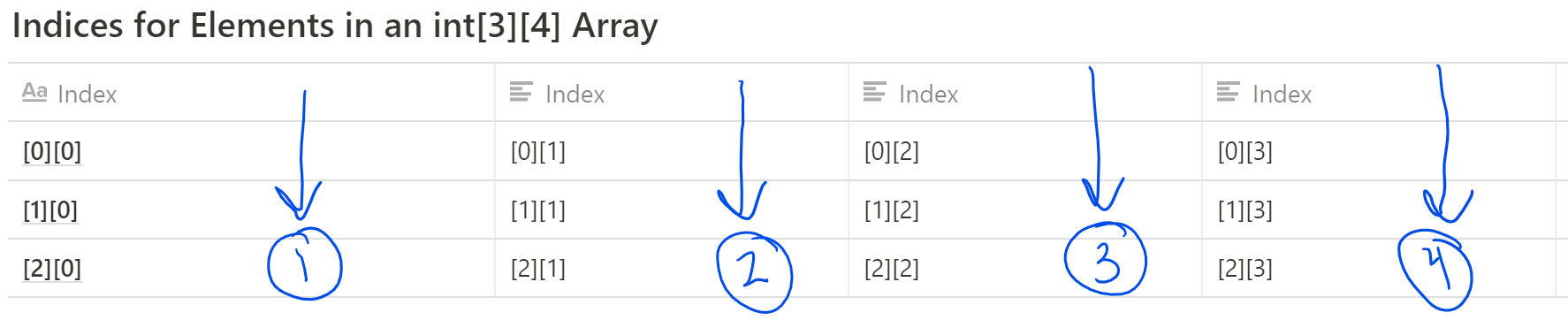
We will focus on traversing in a forward direction (from left-to-right and from top-to-bottom) in this section. In the next, we will go in reverse directions, but this will only require a change in the for loop conditional.
Row-Wise Traversal
When doing row-wise traversal, the outer loop traverses through the different rows, and the inner loop traverses through the elements in each row. Here is how you write code for this:
public static void rowWiseForward(int[][] array) {
for (int i = 0; i < array.length; i++) {
for (int j = 0; j < array[0].length; j++) {
System.out.print(array[i][j] + " ");
}
}
}
public static void main(str[] args) {
rowWiseForward(arrayB);
}
1 2 3 4 5 6 7 8 9 10 11 12
We can only use nested enhanced for loops for forward row-wise traversals. Here is the code that creates the same output as above, only this time using enhanced for loops instead of regular for loops:
public static void rowWiseForwardEnhancedForLoops(int[][] array) {
for (int[] row: array) {
for (int number: row) {
System.out.print(number + " ");
}
}
}
Remember that the type of the rows in the 2D array are 1D arrays, and the rows contain elements of a certain type!
Column-Wise Traversal
When doing column-wise traversal, the outer loop traverses through the different columns, and the inner loop traverses through the elements in each columns. Here is how you write code for this:
public static void columnWiseForward(int[][] array) {
for (int i = 0; i < array[0].length; i++) {
for (int j = 0; j < array.length; j++) {
System.out.print(array[j][i] + " ");
}
}
}
public static void main(str[] args) {
columnWiseForward(arrayB);
}
1 5 9 2 6 10 3 7 11 4 8 12
In Summary
We can see that the two traversal algorithms using regular for loops are almost the same. The only significant difference is with the order of the for loop conditionals. However, the loop conditional for traversing through different rows is the same in both cases, and so is the conditional for traversing through different columns. Here are the conditionals for the two different traversal directions:
To traverse through different rows: i < array.length;
To traverse through different columns: i < array[0].length;
We will use this to help us go in reverse next!
Going In Reverse
Sometimes, we want to traverse across the rows from right to left, or traverse across the columns from bottom to top. This will require a change the for loop headers, as follows:
To traverse through different rows: int i = array.length() - 1; i >= 0; i--
This is initializing i to the last row, and then going up row-by-row to the first row in every loop iteration.
To traverse through different columns: int i = array[0].length - 1; i >= 0; i--
Likewise, this is initializing i to the rightmost column, and then going left column-by-column to the first column in every loop iteration.
To do row-wise traversal, put the row for loop header first, while to do column-wise traversal, put the column for loop header first.
Challenge Example: Snaking Around
Let's do a challenge. We want to traverse arrayB so that it prints the following:
1. 1 2 3 4 8 7 6 5 9 10 11 12
2. 12 8 4 3 7 11 10 6 2 1 5 9
For example 1, we are doing a row-wise traversal from top to bottom that starts forward, but then alternates the direction every row as shown in this image:

For example 2, we are doing a column-wise traversal from right to left that starts backwards then alternates in direction as is shown in this image:

What's the secret behind this? It's an if statement and modulo. Here is the code with the this part commented:
public static void exampleOne(int[][] array) {
for (int i = 0; i < array.length; i++) {
if (i % 2 == 0) { // we use an if statement with modulo base 2 to alternate
for (int j = 0; j < array[0].length; j++) {
System.out.print(array[i][j] + " ");
}
} else {
for (int j = array[0].length - 1; j >= 0; j--) {
System.out.print(array[i][j] + " ");
}
}
}
}
public static void exampleTwo(int[][] array) {
for (int i = array[0].length - 1; i >= 0; i--) {
if (i % 2 == 0) { // we use an if statement with modulo base 2 to alternate
for (int j = 0; j < array[0].length - 1; j++) {
System.out.print(array[j][i] + " ");
}
} else {
for (int j = array.length - 1; j >= 0; j--) {
System.out.print(array[j][i] + " ");
}
}
}
}
Standard Algorithms Using Traversals
For 2D arrays, we use the slightly modified versions of the algorithms we have been doing with 1D arrays and ArrayLists. All of these algorithms apply the loop traversals we have just discussed! Here, we will have a snippet for each algorithm you are expected to know with each snippet annotated for you.
Sequential/Linear Search
/** Prints the row and column indices if the element is in the array and -1 if not
*/
public static boolean searchForElement(int[][] array, int elementToSearch) {
flag = false; //sets flag to see if element has been found
for (int i = 0; i < array.length; i++) {
for (int j = 0; j < array[0].length; j++) { //traverses through the array
if (array[i][j] == elementToSearch) {
System.out.println("Row " + i);
System.out.println("Column " + j); //if element found, print coordinates
return true; //element has been found
}
}
}
if (!flag) { //if element not found, return false
return false;
}
}
Modifying Array Values
/** Doubles each element of the array
*/
public static void doubleArray(int[][] array) {
for (int i = 0; i < array.length; i++) {
for (int j = 0; j < array[0].length; j++) {
array[i][j] *= 2; // doubles each individual element
}
}
}
Note that in the above snippet, we used regular for loops instead of enhanced for loops. Here, we cannot use enhanced for loops as follows:
/** Doubles each element of the array
*/
public static void doubleArray(int[][] array) {
for (int[] row: array) {
for (int number: row) {
number *= 2; // doubles number
}
}
}
This is because Java is pass-by-value. In the first example, we are actually accessing the array itself. However, in the enhanced for loop example, we are making a copy of that array and any changes are affecting the copy, not the actual array.
However, if the array items are objects and we are changing the value of one of the object's instance variables, we can use enhanced for loops as the copy contains references to the actual objects themselves. Here is an example of this:
/** Represents a student
*/
public class Student {
private String name;
/** Sets the name of the Student
*/
public void setName(String name) {
this.name = name;
}
/** Other instance variables, methods, and constructors not shown
*/
}
// IN ANOTHER CLASS
/** Resets names of all student s
*/
public static void doubleArray(Student[][] array, String defaultName) {
for (Student[] row: array) {
for (Student student: row) {
student.setName(defaultName); // Sets each student's name to a default name
}
}
}
Putting all the Values Into an ArrayList
/** Inserts all the values in the array into an ArrayList
*/
public static ArrayList<Integer> putIntoArrayList(int[][] array) {
ArrayList<Integer> intList = new ArrayList<Integer>(); //makes an empty ArrayList
for (int[] row: array) {
for (int number: row) {
//Boxes the integer to an Integer object adding it to the ArrayList
intList.add(new Integer(number));
}
}
return intList;
}
Java has autoboxing, so you could also just do intList.add(number); and Java will automatically convert the integer into an Integer object.
Putting all the Values Into an Array
/** Inserts all the values in the array into an array
*/
public static int[] putIntoArray(int[][] array) {
int[] intArray = new int[array.length * array[0].length]; //initialize the array
for (int i = 0; i < array.length; i++) { //to the number of items in rect array
for (int j = 0; j < array[0].length; j++) {
//i*array[0].length + j is the nth item
intArray[i*array[0].length + j] = array[i][j];
}
}
return intArray;
}
Finding the Minimum and Maximum
/** Finds the maximum
*/
public static int maximum(int[][] array) {
int maxValue = array[0][0];
for (int[] row: array) {
for (int number: row) {
if (number > maxValue) { //if new max value found, replace current maxValue
maxValue = number;
}
}
}
return maxValue;
}
/** Finds the minimum
*/
public static int minimum(int[][] array) {
int minValue = array[0][0];
for (int[] row: array) {
for (int number: row) {
if (number < minValue) { //if new min value found, replace current minValue
minValue = number;
}
}
}
return minValue;
}
A common mistake is initializing the maxValue and minValue to 0.
If all the values in the array are positive, it would incorrectly keep minValue at 0 (all the values are greater than 0, leaving 0 as the minimum).
If all the values in the array are negative, it would incorrectly keep maxValue at 0 (all the values are less than 0, leaving 0 as the maximum).
To counter these errors, initialize these to the first value in the array.
Finding a Sum
/** Sums up all elements in the array
*/
public static int sum(int[][] array) {
int sum = 0;
for (int[] row: array) {
for (int number: row) {
sum += number; //adds every element to sum
}
}
return sum;
}
Finding a Mean
/** Finds the mean/average of the array
*/
public static int mean(int[][] array) {
// find the sum of the array, can be replaced with sum algorithm above
int sum = sum(array);
return (double) sum / (array.length * array[0].length);
}
Finding a Mode
/** Finds the mode of an array
Prerequisite: The array must have a mode
*/
public static int mode(int[][] array) {
int[] newArray = putIntoArray(array) //places the numbers into a 1D array as above
int mostCommon = 0;
int mostCommonFrequency = 0;
for (int i = 0; i < newArray.length - 1; i++) { //traverse through the new array
int currentFrequency = 1;
for (int j = i + 1; j < newArray.length; j++) { //traverse through rest of array
// if any element matches current element being checked, add 1 to frequency
if (newArray[j] == newArray[i]) {
currentFrequency++;
}
}
if (currentFrequency > mostCommonFrequency) {
mostCommon = newArray[i]; // replaces current mode if new most common element
mostCommonFrequency = currentFrequency;
}
}
return mostCommon; // can also be modified to return the frequency
}
Determining If All Values Have a Certain Property
/** Determines whether all values are even
*/
public static boolean isEven(int[][] array) {
//Assume all values are positive first
for (int[] row: array) {
for (int number: row) {
if (number % 2 == 1) { //If there is one value that is not positive, return false
return false;
}
}
}
return true; //No odd numbers were found
}
Accessing All Consecutive Pairs/Triplets/Sequences of Length n of Elements
/** Returns all consecutive sequences of length n in the array
*/
public static void returnAllConsecutiveSequences(int[][] array, int length) {
public int[] oneDArray = putIntoArray(array);
for (int i = 0; i <= oneDArray.length - length; i++) {
for (int j = 0; j < length; j++) {
System.out.print(oneDArray[i+j] + " "); //2 loops, one to get the starting number
} //the other to go through the sequences
System.out.println();
}
}
Checking if There are Duplicate Elements
/** Checks to see if there are duplicate elements
*/
public static boolean duplicates(int[][] array) {
int[] newArray = putIntoArray(array) //places the numbers into a 1D array as above
for (int i = 0; i < newArray.length - 1; i++) { //traverse through the new array
for (int j = i + 1; j < newArray.length; j++) { //traverse through rest of array
// if any element matches current element being checked, return true
if (newArray[j] == newArray[i]) {
return true;
}
}
}
return false; // if this point reached, no duplicates found
}
Determining How Many Elements Fit a Criteria
/** Returns how many even numbers there are
*/
public static int evenFrequency(int[][] array) {
int numberEven = 0;
for (int[] row: array) {
for (int number: row) {
if (number % 2 == 0) {
numberEven++; // increments every time an even integer is found
}
}
}
return numberEven;
}
<< Hide Menu
Avanish Gupta
Milo Chang
Avanish Gupta
Milo Chang
Note: In this topic, we will be using arrayB and the graphical representation of 2D arrays from the previous topic. As a reminder, here is arrayB:
int[][] arrayB = {{1, 2, 3, 4},
{5, 6, 7, 8},
{9, 10, 11, 12}};
General Form
Recall that when traversing a 1D array, you use a loop, usually a for loop or enhanced for loop. This is similar to how we traverse 2D arrays, except in 2D arrays, we need 2 nested for loops, an outer loop traversing through one dimension, and an inner loop traversing through the other. Here is the general form:
for (firstDimension traversal conditions) {
for (secondDimension traversal conditions) {
System.out.print(item + " ");
}
}
System.out.println();
Row-Major vs. Column-Major
There are two main directions we can traverse through. The first is row-major traversal, traversing through every element in one row before moving to the next. Conversely, there is column-major traversal, traversing through every element in one column before moving on to the next.
Row-wise Traversal

Column-wise Traversal

We will focus on traversing in a forward direction (from left-to-right and from top-to-bottom) in this section. In the next, we will go in reverse directions, but this will only require a change in the for loop conditional.
Row-Wise Traversal
When doing row-wise traversal, the outer loop traverses through the different rows, and the inner loop traverses through the elements in each row. Here is how you write code for this:
public static void rowWiseForward(int[][] array) {
for (int i = 0; i < array.length; i++) {
for (int j = 0; j < array[0].length; j++) {
System.out.print(array[i][j] + " ");
}
}
}
public static void main(str[] args) {
rowWiseForward(arrayB);
}
1 2 3 4 5 6 7 8 9 10 11 12
We can only use nested enhanced for loops for forward row-wise traversals. Here is the code that creates the same output as above, only this time using enhanced for loops instead of regular for loops:
public static void rowWiseForwardEnhancedForLoops(int[][] array) {
for (int[] row: array) {
for (int number: row) {
System.out.print(number + " ");
}
}
}
Remember that the type of the rows in the 2D array are 1D arrays, and the rows contain elements of a certain type!
Column-Wise Traversal
When doing column-wise traversal, the outer loop traverses through the different columns, and the inner loop traverses through the elements in each columns. Here is how you write code for this:
public static void columnWiseForward(int[][] array) {
for (int i = 0; i < array[0].length; i++) {
for (int j = 0; j < array.length; j++) {
System.out.print(array[j][i] + " ");
}
}
}
public static void main(str[] args) {
columnWiseForward(arrayB);
}
1 5 9 2 6 10 3 7 11 4 8 12
In Summary
We can see that the two traversal algorithms using regular for loops are almost the same. The only significant difference is with the order of the for loop conditionals. However, the loop conditional for traversing through different rows is the same in both cases, and so is the conditional for traversing through different columns. Here are the conditionals for the two different traversal directions:
To traverse through different rows: i < array.length;
To traverse through different columns: i < array[0].length;
We will use this to help us go in reverse next!
Going In Reverse
Sometimes, we want to traverse across the rows from right to left, or traverse across the columns from bottom to top. This will require a change the for loop headers, as follows:
To traverse through different rows: int i = array.length() - 1; i >= 0; i--
This is initializing i to the last row, and then going up row-by-row to the first row in every loop iteration.
To traverse through different columns: int i = array[0].length - 1; i >= 0; i--
Likewise, this is initializing i to the rightmost column, and then going left column-by-column to the first column in every loop iteration.
To do row-wise traversal, put the row for loop header first, while to do column-wise traversal, put the column for loop header first.
Challenge Example: Snaking Around
Let's do a challenge. We want to traverse arrayB so that it prints the following:
1. 1 2 3 4 8 7 6 5 9 10 11 12
2. 12 8 4 3 7 11 10 6 2 1 5 9
For example 1, we are doing a row-wise traversal from top to bottom that starts forward, but then alternates the direction every row as shown in this image:

For example 2, we are doing a column-wise traversal from right to left that starts backwards then alternates in direction as is shown in this image:

What's the secret behind this? It's an if statement and modulo. Here is the code with the this part commented:
public static void exampleOne(int[][] array) {
for (int i = 0; i < array.length; i++) {
if (i % 2 == 0) { // we use an if statement with modulo base 2 to alternate
for (int j = 0; j < array[0].length; j++) {
System.out.print(array[i][j] + " ");
}
} else {
for (int j = array[0].length - 1; j >= 0; j--) {
System.out.print(array[i][j] + " ");
}
}
}
}
public static void exampleTwo(int[][] array) {
for (int i = array[0].length - 1; i >= 0; i--) {
if (i % 2 == 0) { // we use an if statement with modulo base 2 to alternate
for (int j = 0; j < array[0].length - 1; j++) {
System.out.print(array[j][i] + " ");
}
} else {
for (int j = array.length - 1; j >= 0; j--) {
System.out.print(array[j][i] + " ");
}
}
}
}
Standard Algorithms Using Traversals
For 2D arrays, we use the slightly modified versions of the algorithms we have been doing with 1D arrays and ArrayLists. All of these algorithms apply the loop traversals we have just discussed! Here, we will have a snippet for each algorithm you are expected to know with each snippet annotated for you.
Sequential/Linear Search
/** Prints the row and column indices if the element is in the array and -1 if not
*/
public static boolean searchForElement(int[][] array, int elementToSearch) {
flag = false; //sets flag to see if element has been found
for (int i = 0; i < array.length; i++) {
for (int j = 0; j < array[0].length; j++) { //traverses through the array
if (array[i][j] == elementToSearch) {
System.out.println("Row " + i);
System.out.println("Column " + j); //if element found, print coordinates
return true; //element has been found
}
}
}
if (!flag) { //if element not found, return false
return false;
}
}
Modifying Array Values
/** Doubles each element of the array
*/
public static void doubleArray(int[][] array) {
for (int i = 0; i < array.length; i++) {
for (int j = 0; j < array[0].length; j++) {
array[i][j] *= 2; // doubles each individual element
}
}
}
Note that in the above snippet, we used regular for loops instead of enhanced for loops. Here, we cannot use enhanced for loops as follows:
/** Doubles each element of the array
*/
public static void doubleArray(int[][] array) {
for (int[] row: array) {
for (int number: row) {
number *= 2; // doubles number
}
}
}
This is because Java is pass-by-value. In the first example, we are actually accessing the array itself. However, in the enhanced for loop example, we are making a copy of that array and any changes are affecting the copy, not the actual array.
However, if the array items are objects and we are changing the value of one of the object's instance variables, we can use enhanced for loops as the copy contains references to the actual objects themselves. Here is an example of this:
/** Represents a student
*/
public class Student {
private String name;
/** Sets the name of the Student
*/
public void setName(String name) {
this.name = name;
}
/** Other instance variables, methods, and constructors not shown
*/
}
// IN ANOTHER CLASS
/** Resets names of all student s
*/
public static void doubleArray(Student[][] array, String defaultName) {
for (Student[] row: array) {
for (Student student: row) {
student.setName(defaultName); // Sets each student's name to a default name
}
}
}
Putting all the Values Into an ArrayList
/** Inserts all the values in the array into an ArrayList
*/
public static ArrayList<Integer> putIntoArrayList(int[][] array) {
ArrayList<Integer> intList = new ArrayList<Integer>(); //makes an empty ArrayList
for (int[] row: array) {
for (int number: row) {
//Boxes the integer to an Integer object adding it to the ArrayList
intList.add(new Integer(number));
}
}
return intList;
}
Java has autoboxing, so you could also just do intList.add(number); and Java will automatically convert the integer into an Integer object.
Putting all the Values Into an Array
/** Inserts all the values in the array into an array
*/
public static int[] putIntoArray(int[][] array) {
int[] intArray = new int[array.length * array[0].length]; //initialize the array
for (int i = 0; i < array.length; i++) { //to the number of items in rect array
for (int j = 0; j < array[0].length; j++) {
//i*array[0].length + j is the nth item
intArray[i*array[0].length + j] = array[i][j];
}
}
return intArray;
}
Finding the Minimum and Maximum
/** Finds the maximum
*/
public static int maximum(int[][] array) {
int maxValue = array[0][0];
for (int[] row: array) {
for (int number: row) {
if (number > maxValue) { //if new max value found, replace current maxValue
maxValue = number;
}
}
}
return maxValue;
}
/** Finds the minimum
*/
public static int minimum(int[][] array) {
int minValue = array[0][0];
for (int[] row: array) {
for (int number: row) {
if (number < minValue) { //if new min value found, replace current minValue
minValue = number;
}
}
}
return minValue;
}
A common mistake is initializing the maxValue and minValue to 0.
If all the values in the array are positive, it would incorrectly keep minValue at 0 (all the values are greater than 0, leaving 0 as the minimum).
If all the values in the array are negative, it would incorrectly keep maxValue at 0 (all the values are less than 0, leaving 0 as the maximum).
To counter these errors, initialize these to the first value in the array.
Finding a Sum
/** Sums up all elements in the array
*/
public static int sum(int[][] array) {
int sum = 0;
for (int[] row: array) {
for (int number: row) {
sum += number; //adds every element to sum
}
}
return sum;
}
Finding a Mean
/** Finds the mean/average of the array
*/
public static int mean(int[][] array) {
// find the sum of the array, can be replaced with sum algorithm above
int sum = sum(array);
return (double) sum / (array.length * array[0].length);
}
Finding a Mode
/** Finds the mode of an array
Prerequisite: The array must have a mode
*/
public static int mode(int[][] array) {
int[] newArray = putIntoArray(array) //places the numbers into a 1D array as above
int mostCommon = 0;
int mostCommonFrequency = 0;
for (int i = 0; i < newArray.length - 1; i++) { //traverse through the new array
int currentFrequency = 1;
for (int j = i + 1; j < newArray.length; j++) { //traverse through rest of array
// if any element matches current element being checked, add 1 to frequency
if (newArray[j] == newArray[i]) {
currentFrequency++;
}
}
if (currentFrequency > mostCommonFrequency) {
mostCommon = newArray[i]; // replaces current mode if new most common element
mostCommonFrequency = currentFrequency;
}
}
return mostCommon; // can also be modified to return the frequency
}
Determining If All Values Have a Certain Property
/** Determines whether all values are even
*/
public static boolean isEven(int[][] array) {
//Assume all values are positive first
for (int[] row: array) {
for (int number: row) {
if (number % 2 == 1) { //If there is one value that is not positive, return false
return false;
}
}
}
return true; //No odd numbers were found
}
Accessing All Consecutive Pairs/Triplets/Sequences of Length n of Elements
/** Returns all consecutive sequences of length n in the array
*/
public static void returnAllConsecutiveSequences(int[][] array, int length) {
public int[] oneDArray = putIntoArray(array);
for (int i = 0; i <= oneDArray.length - length; i++) {
for (int j = 0; j < length; j++) {
System.out.print(oneDArray[i+j] + " "); //2 loops, one to get the starting number
} //the other to go through the sequences
System.out.println();
}
}
Checking if There are Duplicate Elements
/** Checks to see if there are duplicate elements
*/
public static boolean duplicates(int[][] array) {
int[] newArray = putIntoArray(array) //places the numbers into a 1D array as above
for (int i = 0; i < newArray.length - 1; i++) { //traverse through the new array
for (int j = i + 1; j < newArray.length; j++) { //traverse through rest of array
// if any element matches current element being checked, return true
if (newArray[j] == newArray[i]) {
return true;
}
}
}
return false; // if this point reached, no duplicates found
}
Determining How Many Elements Fit a Criteria
/** Returns how many even numbers there are
*/
public static int evenFrequency(int[][] array) {
int numberEven = 0;
for (int[] row: array) {
for (int number: row) {
if (number % 2 == 0) {
numberEven++; // increments every time an even integer is found
}
}
}
return numberEven;
}

© 2024 Fiveable Inc. All rights reserved.