Browse By Unit
9.9 Finding the Area of the Region Bounded by Two Polar Curves
3 min read•june 18, 2024
9.9 Finding the Area of the Region Bounded by Two Polar Curves
Welcome to the last topic of the 9th unit! In this key topic, we’ll be learning more about polar functions and how to find the area between two polar curves and how it’s different from finding the area between two normal curves plotted on the x-y plane. 📈
For a review of how to find the area of a polar region with one curve, see topic 9.8!
⭕ Equation for Area of One vs. Two Curves
The equation for area for one curve, as mentioned in 9.8, was the following:
Where and represent your polar interval and represents the radius of the curve which will be given.
How will you edit this formula to account for two curves 🤔? Just include the difference of the radii! Here is the updated formula:
In this case, is the outside radius and is the inside radius. Your boundaries will be where .
📝 Area Between 2 Polar Curves Example Walkthrough
Here’s the question! Let be the region bounded between and in the second quadrant. Find the area between the two functions pictured in the graph below.

Image Courtesy of Desmos
1️⃣ Define your and functions!
This is very important as you want to determine which function is the inside function and the outside function to simplify your calculations as much as possible! 😊
For a hint on how to determine the outside and inside function, picture yourself at the origin. What function do you see first from the origin? That’s your inside function! What function do you see past that first function? That’s your outside function!
Since we are trying to find the area in the second quadrant, from the origin, the circle is seen first and is the inner ⬅️ function. The other function is therefore the outer ➡️ function!
2️⃣ Determine the bounds for the area!
Remember the polar coordinate system? Here it is below for your reference.
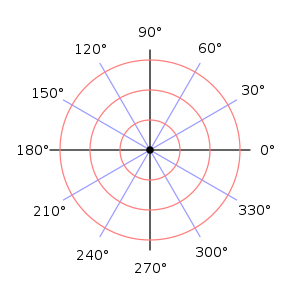
Image Courtesy of Wikipedia
Basically, the distance from the origin is your radius and the angle from the positive x-axis is your θ value.
On the original graph, we can see that the region can be one of two sections.
First we have to determine what section of the graph we have to focus on. The question says second quadrant, therefore your bounds will be from to !
For a more systematic way to determine bounds, set the two equations equal to each other and determine your angles.
Again, since the problem mentions the second quadrant, you only need to choose the bounds of the second quadrant and again we get to !
3️⃣ Set up your integral and evaluate!
Now that you have your bounds and your functions, all that’s left is to plug in values to your formula and evaluate!
For this part, if it is a tough integral, you will usually just have to set up the integral on a non-calculator question or evaluate the integral in your calculator for the calculator section 🔢!
📕 Closing Thoughts
For a non-calculator question, you will most likely be exposed to simple integrals that involve some theorems, such as double angle theorem, etc.! Keep practicing those and you’ll be a total pro at the polar coordinate system ⭕!
So hey, you’ve made it to the end of this unit and you only have one more unit to go! Woohoo! 🥳 Keep working hard and staying amazing! 😊

<< Hide Menu
9.9 Finding the Area of the Region Bounded by Two Polar Curves
3 min read•june 18, 2024
9.9 Finding the Area of the Region Bounded by Two Polar Curves
Welcome to the last topic of the 9th unit! In this key topic, we’ll be learning more about polar functions and how to find the area between two polar curves and how it’s different from finding the area between two normal curves plotted on the x-y plane. 📈
For a review of how to find the area of a polar region with one curve, see topic 9.8!
⭕ Equation for Area of One vs. Two Curves
The equation for area for one curve, as mentioned in 9.8, was the following:
Where and represent your polar interval and represents the radius of the curve which will be given.
How will you edit this formula to account for two curves 🤔? Just include the difference of the radii! Here is the updated formula:
In this case, is the outside radius and is the inside radius. Your boundaries will be where .
📝 Area Between 2 Polar Curves Example Walkthrough
Here’s the question! Let be the region bounded between and in the second quadrant. Find the area between the two functions pictured in the graph below.

Image Courtesy of Desmos
1️⃣ Define your and functions!
This is very important as you want to determine which function is the inside function and the outside function to simplify your calculations as much as possible! 😊
For a hint on how to determine the outside and inside function, picture yourself at the origin. What function do you see first from the origin? That’s your inside function! What function do you see past that first function? That’s your outside function!
Since we are trying to find the area in the second quadrant, from the origin, the circle is seen first and is the inner ⬅️ function. The other function is therefore the outer ➡️ function!
2️⃣ Determine the bounds for the area!
Remember the polar coordinate system? Here it is below for your reference.

Image Courtesy of Wikipedia
Basically, the distance from the origin is your radius and the angle from the positive x-axis is your θ value.
On the original graph, we can see that the region can be one of two sections.
First we have to determine what section of the graph we have to focus on. The question says second quadrant, therefore your bounds will be from to !
For a more systematic way to determine bounds, set the two equations equal to each other and determine your angles.
Again, since the problem mentions the second quadrant, you only need to choose the bounds of the second quadrant and again we get to !
3️⃣ Set up your integral and evaluate!
Now that you have your bounds and your functions, all that’s left is to plug in values to your formula and evaluate!
For this part, if it is a tough integral, you will usually just have to set up the integral on a non-calculator question or evaluate the integral in your calculator for the calculator section 🔢!
📕 Closing Thoughts
For a non-calculator question, you will most likely be exposed to simple integrals that involve some theorems, such as double angle theorem, etc.! Keep practicing those and you’ll be a total pro at the polar coordinate system ⭕!
So hey, you’ve made it to the end of this unit and you only have one more unit to go! Woohoo! 🥳 Keep working hard and staying amazing! 😊


© 2024 Fiveable Inc. All rights reserved.