Browse By Unit
9.4 Defining and Differentiating Vector-Valued Functions
6 min read•june 18, 2024
9.4 Defining and Differentiating Vector-Valued Functions
So far in this unit, we’ve been delving deep into the functions of parametric equations. Now, we’re taking this knowledge and talking about vector-valued functions!
↖️ Vector Review
A vector is a quantity that has both direction and magnitude. Magnitude refers to the length of a vector. All vectors have horizontal and vertical components. They are written and defined based on these two components. For example, a vector with a horizontal component of 5 and a vertical component of 4 would be written as . While there are a couple of other methods of writing vectors, this kind of notation is used most frequently on the AP Calculus BC Exam!
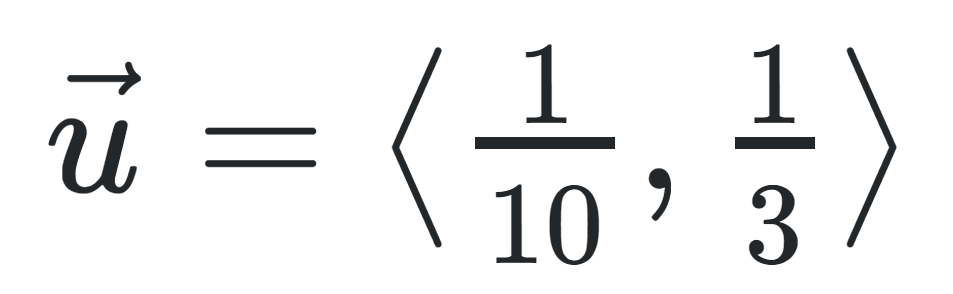
Image Courtesy of LaTeX Stack Exchange
Every vector is drawn with a head and a tail. The tail of the vector is the point at which the vector originates. If there is no additional information given, we can assume that the vector originates from (0,0) and that the tail of the vector is at (0,0). The head of the vector is the final point of the vector. In diagrams, the head of the vector is represented with an arrowhead.

Image Courtesy of Labster
The magnitude of the vector can be calculated based on the horizontal and vertical components of the vector. Let’s find the magnitude of the vector we used earlier, . This vector has a horizontal component of 5 and a vertical component of 4. We can find the magnitude by using the Pythagorean theorem and calculating for the hypotenuse. The Pythagorean theorem is . In this scenario, and . Therefore, . The magnitude of our vector is . The magnitude of the vector is written as ‖𝑣‖.
We can also calculate the direction of the vector from its horizontal and vertical components. We know that . For our example vector from earlier, . Using inverse tangent, we can calculate that .
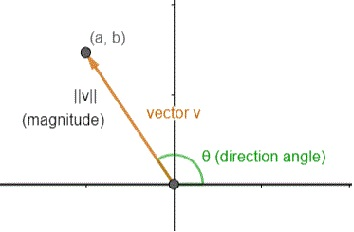
Image Courtesy of Study.com
We have now seen that we can calculate the magnitude and direction of a vector given its horizontal and vertical components. Similarly, we can also calculate the horizontal and vertical components from the magnitude and direction of the vector.
📐 Vector-Valued Functions
Think of as a vector composed of the two parametric functions and . We can write the vector as If we wanted to differentiate this vector-valued function, we can write the derivative of the function as . Normal derivation rules apply to vector-valued functions! These rules are summarized in the image below.

Image Courtesy of the Algebros
✏️ Vector-Valued Functions Walkthrough
Let’s do a quick example!
Find
Since we are asked to find , let’s begin by finding . We do this by taking the derivative of each of the components. We can start with the horizontal component, . The derivative of with respect to is .
The vertical component of is . The derivative of with respect to is .
Now, let’s put it all together!
We can then substitute for to find .
And now we simplify!
Now that we know a bit about vectors and vector-valued functions, let’s amp it up and try some practice problems :)
🤔 Practice Problems with Vector-Valued Functions
We have to two practice problems embedded in this study guide for you!
💭 Vector Practice Problem 1
Find given that
Let’s begin by finding the derivative of each of the components. We can start with the horizontal component, . The derivative of with respect to is .
The vertical component of is . The derivative of with respect to is .
Now, let’s put it all together!
We can then substitute for .
All that’s left to do is simplify!
Great work! Let’s try another practice problem.
💭 Vector Practice Problem 2
A particle moves along a path so that its position at any given time where t≥0 is given by Find the particle’s velocity vector at .
Here’s the solution!
A particle’s velocity vector is the first derivative of its position vector.
Therefore, . To find the particle’s velocity vector at , we can begin by taking the first derivative of the position vector.
We can start with the horizontal component, . The derivative of with respect to is .
The vertical component of is . The derivative of with respect to is .
Like earlier, let’s put it all together!
We can then substitute for .
All that’s left to do is simplify!
As you keep practicing, solving these problems will get easier and easier! Like always, practice is key. 🔑
You got this!!
<< Hide Menu
9.4 Defining and Differentiating Vector-Valued Functions
6 min read•june 18, 2024
9.4 Defining and Differentiating Vector-Valued Functions
So far in this unit, we’ve been delving deep into the functions of parametric equations. Now, we’re taking this knowledge and talking about vector-valued functions!
↖️ Vector Review
A vector is a quantity that has both direction and magnitude. Magnitude refers to the length of a vector. All vectors have horizontal and vertical components. They are written and defined based on these two components. For example, a vector with a horizontal component of 5 and a vertical component of 4 would be written as . While there are a couple of other methods of writing vectors, this kind of notation is used most frequently on the AP Calculus BC Exam!
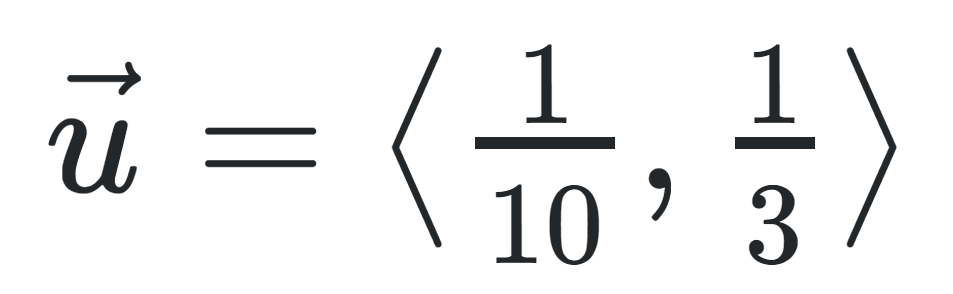
Image Courtesy of LaTeX Stack Exchange
Every vector is drawn with a head and a tail. The tail of the vector is the point at which the vector originates. If there is no additional information given, we can assume that the vector originates from (0,0) and that the tail of the vector is at (0,0). The head of the vector is the final point of the vector. In diagrams, the head of the vector is represented with an arrowhead.

Image Courtesy of Labster
The magnitude of the vector can be calculated based on the horizontal and vertical components of the vector. Let’s find the magnitude of the vector we used earlier, . This vector has a horizontal component of 5 and a vertical component of 4. We can find the magnitude by using the Pythagorean theorem and calculating for the hypotenuse. The Pythagorean theorem is . In this scenario, and . Therefore, . The magnitude of our vector is . The magnitude of the vector is written as ‖𝑣‖.
We can also calculate the direction of the vector from its horizontal and vertical components. We know that . For our example vector from earlier, . Using inverse tangent, we can calculate that .

Image Courtesy of Study.com
We have now seen that we can calculate the magnitude and direction of a vector given its horizontal and vertical components. Similarly, we can also calculate the horizontal and vertical components from the magnitude and direction of the vector.
📐 Vector-Valued Functions
Think of as a vector composed of the two parametric functions and . We can write the vector as If we wanted to differentiate this vector-valued function, we can write the derivative of the function as . Normal derivation rules apply to vector-valued functions! These rules are summarized in the image below.

Image Courtesy of the Algebros
✏️ Vector-Valued Functions Walkthrough
Let’s do a quick example!
Find
Since we are asked to find , let’s begin by finding . We do this by taking the derivative of each of the components. We can start with the horizontal component, . The derivative of with respect to is .
The vertical component of is . The derivative of with respect to is .
Now, let’s put it all together!
We can then substitute for to find .
And now we simplify!
Now that we know a bit about vectors and vector-valued functions, let’s amp it up and try some practice problems :)
🤔 Practice Problems with Vector-Valued Functions
We have to two practice problems embedded in this study guide for you!
💭 Vector Practice Problem 1
Find given that
Let’s begin by finding the derivative of each of the components. We can start with the horizontal component, . The derivative of with respect to is .
The vertical component of is . The derivative of with respect to is .
Now, let’s put it all together!
We can then substitute for .
All that’s left to do is simplify!
Great work! Let’s try another practice problem.
💭 Vector Practice Problem 2
A particle moves along a path so that its position at any given time where t≥0 is given by Find the particle’s velocity vector at .
Here’s the solution!
A particle’s velocity vector is the first derivative of its position vector.
Therefore, . To find the particle’s velocity vector at , we can begin by taking the first derivative of the position vector.
We can start with the horizontal component, . The derivative of with respect to is .
The vertical component of is . The derivative of with respect to is .
Like earlier, let’s put it all together!
We can then substitute for .
All that’s left to do is simplify!
As you keep practicing, solving these problems will get easier and easier! Like always, practice is key. 🔑
You got this!!

© 2024 Fiveable Inc. All rights reserved.