Browse By Unit
8.10 Volume with Disc Method: Revolving Around Other Axes
3 min read•june 18, 2024
8.10 Volume with Disc Method: Revolving Around Other Axes
Welcome back to Fiveable AP Calculus! Today we are adapting the disc method to find volumes of objects that were rotated around an axis. If you want a quick refresher on the original disc method, click here for access to our 8.9 guide.
🌪️Revolving Around Other Axes
Let’s get into it!
⚾ The Basics
By “revolving around other axes” we mean that a function will revolve around either a horizontal (y=5) or vertical (x=3) axis. It is possible to revolve a function around other types of straight lines, but those transformations are more advanced than the scope of AP Calculus. So you might see…
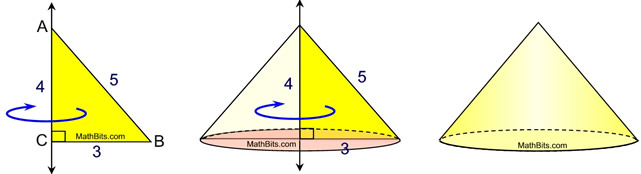
Courtesy of MathBits.com
Or you might see
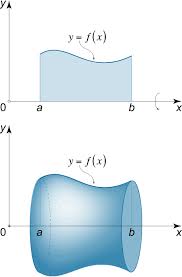
Courtesy of Math24.net
But you won’t have to solve anything more complicated.
🧠 How to Solve
Solving for the volume of a rotated shape with a different horizontal/vertical axis is actually pretty similar to solving for one with a standard x or y-axis! Remember that volume can be represented as an integral by adding up the area of many thin circular cross-sections, and don’t forget to draw out each problem to help you visualize what a rotation looks like.
Step 1: Determine Your Method of Rotation
As a rule of thumb, if you rotate around a horizontal line (such as y=7 or the x-axis), you should write your integral in terms of x, which might look something like . If you are given a vertical line to rotate around, your integral should be written in terms of y and look like.
Just remember, horizontal rotation works with x and vertical rotation works with y!
Step 2: Set Up Your Equation
Just like how we can show a 2D area with by adding a bunch of thin rectangles, we can represent a 3D volume by adding a bunch of thin discs,. The key to setting up your integral is to understand how to calculate the area of these disks! This is where drawing tends to come in handy (don’t worry it doesn’t have to be good).
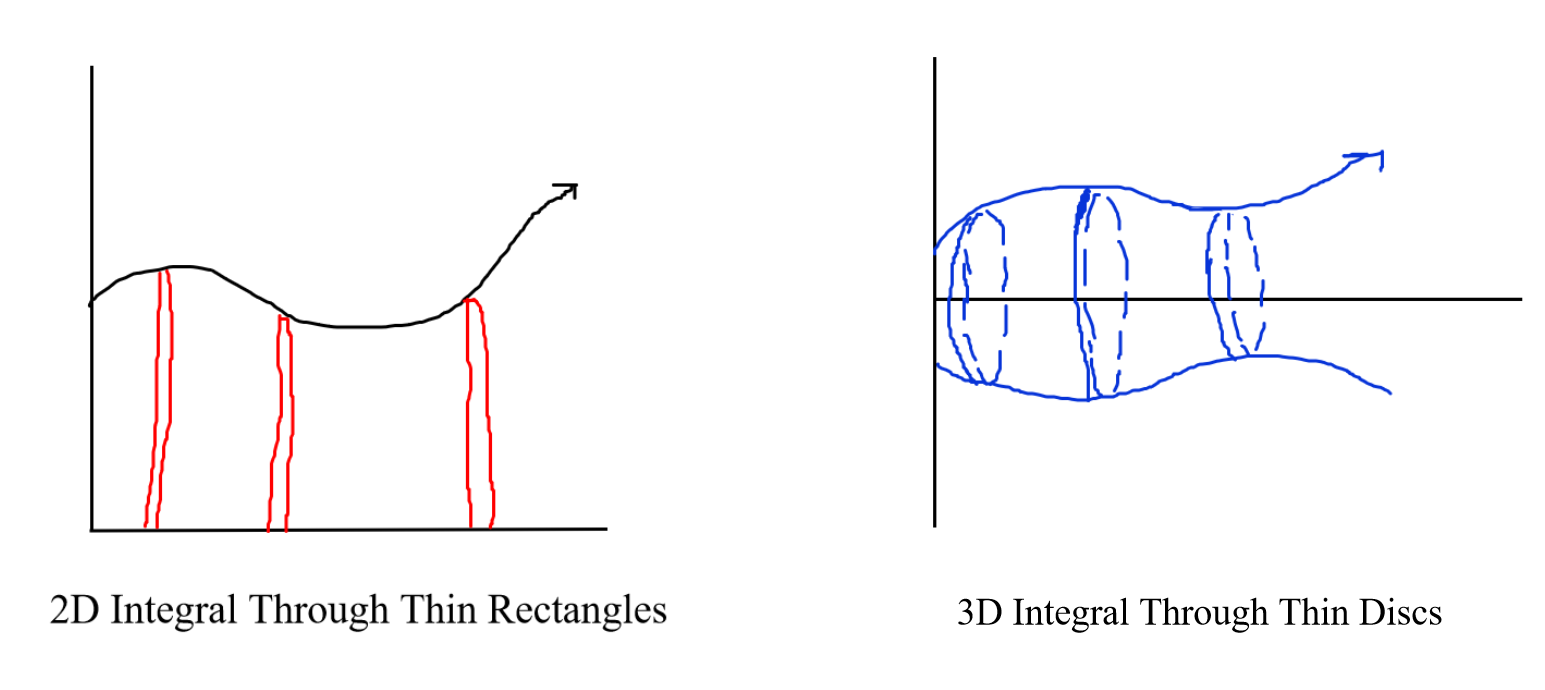
Image Courtesy of Julianna Fontanilla
As you can see on the right, the areas of these discs or cross sections will always be circular since to find them, we take a set distance/radius and rotate it 360 degrees. From basic algebra, we know that the area of a circle equals . From here, we want to find r.
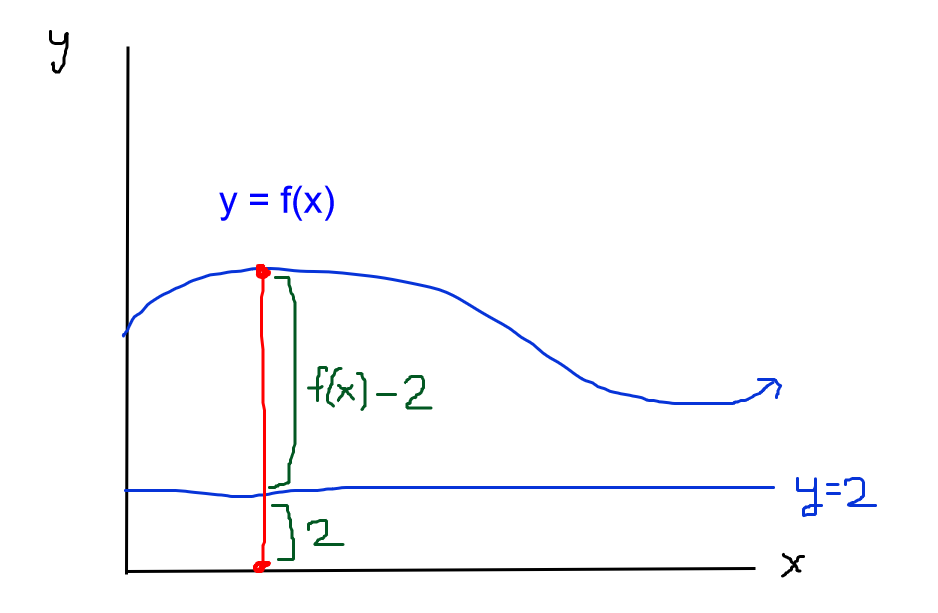
Image Courtesy of Julianna Fontanilla
As you can see in the picture, r is equal to the distance between the function’s value and the axis of rotation. In this example, the axis of rotation is implied to be , since it is a graphed straight line. This means that r can be mathematically represented by , and if the axis of rotation is (where b is some constant), r can be represented by . In the same way, r can also be represented by where the axis of rotation is vertical and equal to
Putting this together with the earlier knowledge that area is , we get that the area in terms of x or y equals or .
Therefore, the integral should look like or ** where the axis of rotation is or .
The upper and lower limit of the integral (c and d) is either outright stated in the problem or occurs at the intersections of f(x) with an axis or another function, maybe g(x). This is visually apparent by graphing each function, but can also be solved algebraically by setting f(x) = g(x) or f(x) = 0 or whatever other line or function that was mentioned in the problem.
👍TL;DR
Just need an equation to memorize? Use one of these integrals:
Use the first equation when rotating around a horizontal axis given as and the second equation for a vertical axis given as . Make sure the square exponent goes outside of the parenthesis, and be mindful that subtracting a negative constant gives a positive value!
🌶️ Practice Time!
Rotate the region bounded by between and about the line .
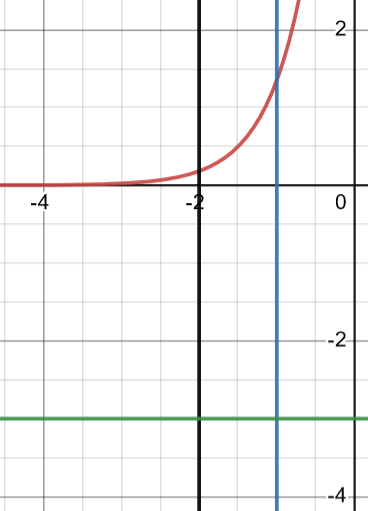
Courtesy of Desmos
Give it a try then scroll down for the solution!
✏️ Answer to Practice Question
We know that the integral’s general format is or . Since we are rotating around a horizontal line (the green one in the picture), we will be using the first equation. Remember that horizontal axes usually use f(x)dx and vertical ones use f(y)dy!
Our upper and lower bounds are given to us directly in the problem, as -2 and -1. We also know that and that the axis of rotation is so
Plugging this into the general format, we get
For more help on how to solve this integral, go here for our guide on integration and accumulation!
First of all, the constant multiple rule for integration states that so the above integral equals
Using FOIL on the middle of the integral gives
Using some basic u-substitution, this integral simplifies to
If you are unsure if you integrated properly, you can always take the derivative of your solution to see if it matches the original!
Our final answer can be found by plugging in -1 and -2 for x, and subtracting appropriately. This gives
which also equals
In a calculator, this is approximately equal to 40.7. Don’t forget to multiply by at the end! You got this! 🍀
<< Hide Menu
8.10 Volume with Disc Method: Revolving Around Other Axes
3 min read•june 18, 2024
8.10 Volume with Disc Method: Revolving Around Other Axes
Welcome back to Fiveable AP Calculus! Today we are adapting the disc method to find volumes of objects that were rotated around an axis. If you want a quick refresher on the original disc method, click here for access to our 8.9 guide.
🌪️Revolving Around Other Axes
Let’s get into it!
⚾ The Basics
By “revolving around other axes” we mean that a function will revolve around either a horizontal (y=5) or vertical (x=3) axis. It is possible to revolve a function around other types of straight lines, but those transformations are more advanced than the scope of AP Calculus. So you might see…

Courtesy of MathBits.com
Or you might see

Courtesy of Math24.net
But you won’t have to solve anything more complicated.
🧠 How to Solve
Solving for the volume of a rotated shape with a different horizontal/vertical axis is actually pretty similar to solving for one with a standard x or y-axis! Remember that volume can be represented as an integral by adding up the area of many thin circular cross-sections, and don’t forget to draw out each problem to help you visualize what a rotation looks like.
Step 1: Determine Your Method of Rotation
As a rule of thumb, if you rotate around a horizontal line (such as y=7 or the x-axis), you should write your integral in terms of x, which might look something like . If you are given a vertical line to rotate around, your integral should be written in terms of y and look like.
Just remember, horizontal rotation works with x and vertical rotation works with y!
Step 2: Set Up Your Equation
Just like how we can show a 2D area with by adding a bunch of thin rectangles, we can represent a 3D volume by adding a bunch of thin discs,. The key to setting up your integral is to understand how to calculate the area of these disks! This is where drawing tends to come in handy (don’t worry it doesn’t have to be good).

Image Courtesy of Julianna Fontanilla
As you can see on the right, the areas of these discs or cross sections will always be circular since to find them, we take a set distance/radius and rotate it 360 degrees. From basic algebra, we know that the area of a circle equals . From here, we want to find r.

Image Courtesy of Julianna Fontanilla
As you can see in the picture, r is equal to the distance between the function’s value and the axis of rotation. In this example, the axis of rotation is implied to be , since it is a graphed straight line. This means that r can be mathematically represented by , and if the axis of rotation is (where b is some constant), r can be represented by . In the same way, r can also be represented by where the axis of rotation is vertical and equal to
Putting this together with the earlier knowledge that area is , we get that the area in terms of x or y equals or .
Therefore, the integral should look like or ** where the axis of rotation is or .
The upper and lower limit of the integral (c and d) is either outright stated in the problem or occurs at the intersections of f(x) with an axis or another function, maybe g(x). This is visually apparent by graphing each function, but can also be solved algebraically by setting f(x) = g(x) or f(x) = 0 or whatever other line or function that was mentioned in the problem.
👍TL;DR
Just need an equation to memorize? Use one of these integrals:
Use the first equation when rotating around a horizontal axis given as and the second equation for a vertical axis given as . Make sure the square exponent goes outside of the parenthesis, and be mindful that subtracting a negative constant gives a positive value!
🌶️ Practice Time!
Rotate the region bounded by between and about the line .

Courtesy of Desmos
Give it a try then scroll down for the solution!
✏️ Answer to Practice Question
We know that the integral’s general format is or . Since we are rotating around a horizontal line (the green one in the picture), we will be using the first equation. Remember that horizontal axes usually use f(x)dx and vertical ones use f(y)dy!
Our upper and lower bounds are given to us directly in the problem, as -2 and -1. We also know that and that the axis of rotation is so
Plugging this into the general format, we get
For more help on how to solve this integral, go here for our guide on integration and accumulation!
First of all, the constant multiple rule for integration states that so the above integral equals
Using FOIL on the middle of the integral gives
Using some basic u-substitution, this integral simplifies to
If you are unsure if you integrated properly, you can always take the derivative of your solution to see if it matches the original!
Our final answer can be found by plugging in -1 and -2 for x, and subtracting appropriately. This gives
which also equals
In a calculator, this is approximately equal to 40.7. Don’t forget to multiply by at the end! You got this! 🍀

© 2024 Fiveable Inc. All rights reserved.