Browse By Unit
8.4 Finding the Area Between Curves Expressed as Functions of x
2 min read•june 18, 2024
8.4 Finding the Area Between Curves Expressed as Functions of x
Welcome back! On both the AB and BC exams, understanding how to evaluate the area between 1 or more functions is essential. In this topic, we will explain exactly how you find the area between two curves in terms of x so you can knock those questions out of the park. 🚀
🔷 The Area Between Curves
When given two functions, you can determine the area between them by subtracting the integral of the bottom function () from the integral of the top function :
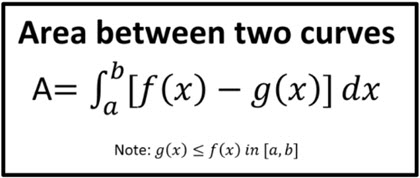
Image Curtesy of Andymath
To determine the upper and lower boundaries of your definite integral, simply find what x-values the two graphs intersect at. This can be done both manually and with a graphing calculator, but you’ll most commonly be asked to use a graphing calculator on the exam.
Let’s go through a question together.
✏️ The Area Between Curves Walkthrough
Find the area between the functions and on the interval .
To start this problem, first, determine which function is greater on the interval, otherwise known as the “top function”. In this case, the graph of is greater than , so we will subtract from .
Replace and with the actual functions!
Now, using the integration techniques you know, integrate and solve the definite integral.
Great job! 🙌
🟦 2022 AP Calc AB FRQ #2a
The following free-response question (FRQ) is from the 2022 AP Calculus AB examination administered by College Board. All credit to College Board.
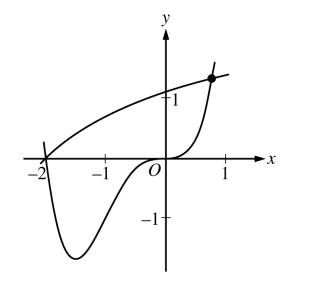
Let f and g be the functions defined by and . The graphs of f and g, shown in the figure above, intersect at and , where .
Find the area of the region enclosed by the graphs of f and g.
🤔 Answering this FRQ
Before you can actually evaluate the definite integral to find the area, we must first find the value of B. Using a graphing calculator, input both the functions and trace them. Afterwards, you can find where both the functions intersect. If you need further guidance as to how to use your graphing calculator, check out our blog, “What Calculator Functions Will Save Your Life?” here.
Doing this, we can find that the value of B is 0.781975. Now, rewrite and evaluate our definite integral to evaluate the area:
⭐Closing
Awesome work! You can now evaluate the area between two functions in terms of x using definite integrals. Understanding how to use your calculator is essential to excelling at this topic, so make sure to look over all of your calculator functions before practicing. 🤗
<< Hide Menu
8.4 Finding the Area Between Curves Expressed as Functions of x
2 min read•june 18, 2024
8.4 Finding the Area Between Curves Expressed as Functions of x
Welcome back! On both the AB and BC exams, understanding how to evaluate the area between 1 or more functions is essential. In this topic, we will explain exactly how you find the area between two curves in terms of x so you can knock those questions out of the park. 🚀
🔷 The Area Between Curves
When given two functions, you can determine the area between them by subtracting the integral of the bottom function () from the integral of the top function :
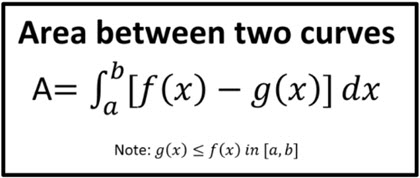
Image Curtesy of Andymath
To determine the upper and lower boundaries of your definite integral, simply find what x-values the two graphs intersect at. This can be done both manually and with a graphing calculator, but you’ll most commonly be asked to use a graphing calculator on the exam.
Let’s go through a question together.
✏️ The Area Between Curves Walkthrough
Find the area between the functions and on the interval .
To start this problem, first, determine which function is greater on the interval, otherwise known as the “top function”. In this case, the graph of is greater than , so we will subtract from .
Replace and with the actual functions!
Now, using the integration techniques you know, integrate and solve the definite integral.
Great job! 🙌
🟦 2022 AP Calc AB FRQ #2a
The following free-response question (FRQ) is from the 2022 AP Calculus AB examination administered by College Board. All credit to College Board.

Let f and g be the functions defined by and . The graphs of f and g, shown in the figure above, intersect at and , where .
Find the area of the region enclosed by the graphs of f and g.
🤔 Answering this FRQ
Before you can actually evaluate the definite integral to find the area, we must first find the value of B. Using a graphing calculator, input both the functions and trace them. Afterwards, you can find where both the functions intersect. If you need further guidance as to how to use your graphing calculator, check out our blog, “What Calculator Functions Will Save Your Life?” here.
Doing this, we can find that the value of B is 0.781975. Now, rewrite and evaluate our definite integral to evaluate the area:
⭐Closing
Awesome work! You can now evaluate the area between two functions in terms of x using definite integrals. Understanding how to use your calculator is essential to excelling at this topic, so make sure to look over all of your calculator functions before practicing. 🤗

© 2024 Fiveable Inc. All rights reserved.