Browse By Unit
6.2 Approximating Areas with Riemann Sums
1 min read•june 18, 2024
Emery
Emery
6.2 Approximating Areas with Riemann Sums
Welcome back to AP Calc with Fiveable! In the last guide, we explored accumulations of change and thought about how to compute them. Here, we’ll take a deep dive into Riemann sums, a method for approximating the area under the curve to find the accumulation of change.
📶 Graphical Riemann Sums
As we delve into integral calculus, our goal has shifted from computing the instantaneous rate of change to computing the area under the curve. Riemann sums are a useful tool for approximating this. Take a look at this graph:
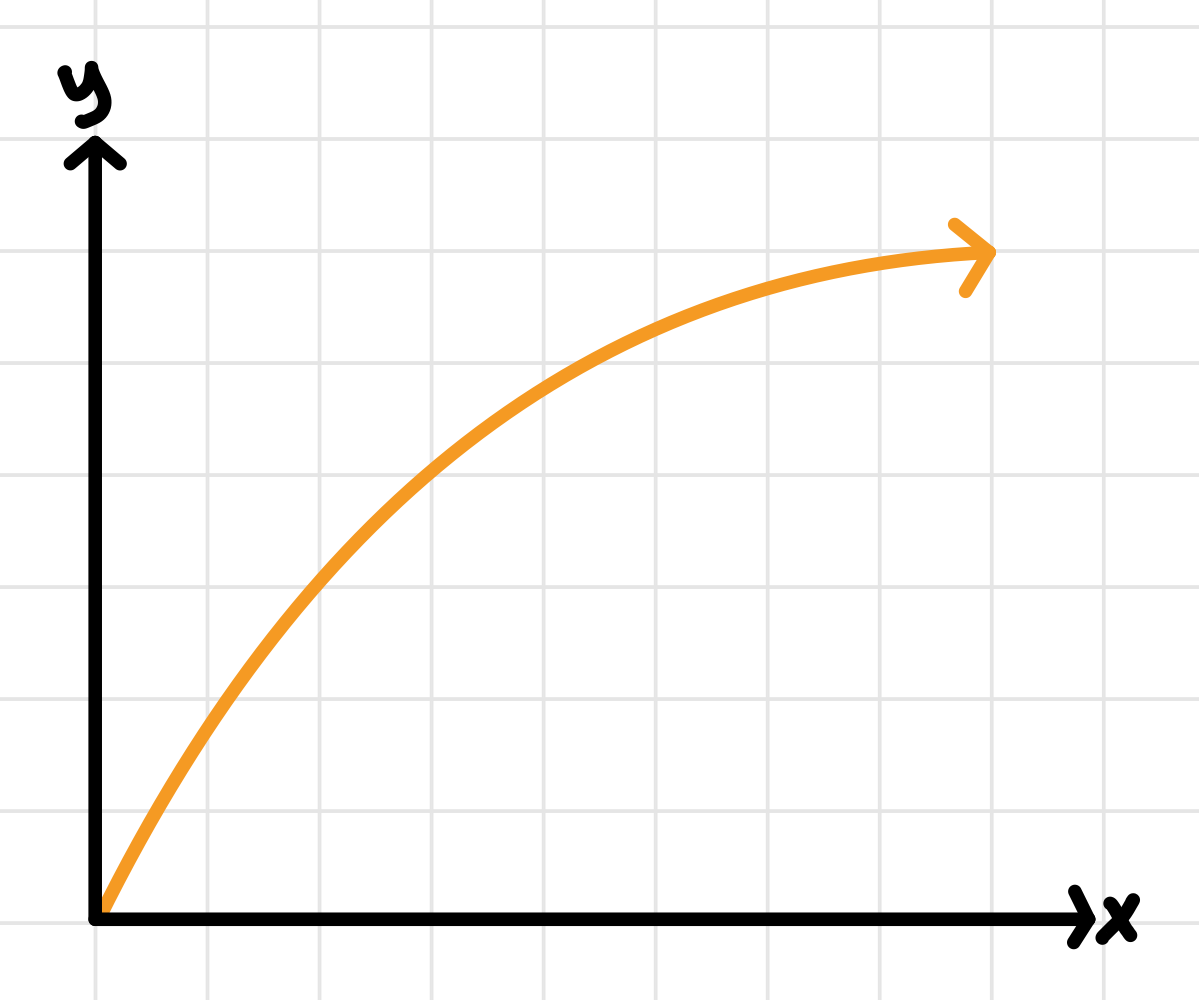
Image courtesy of Emery
You would have a hard time computing this geometrically. But, we can approximate it using familiar shapes, like this:
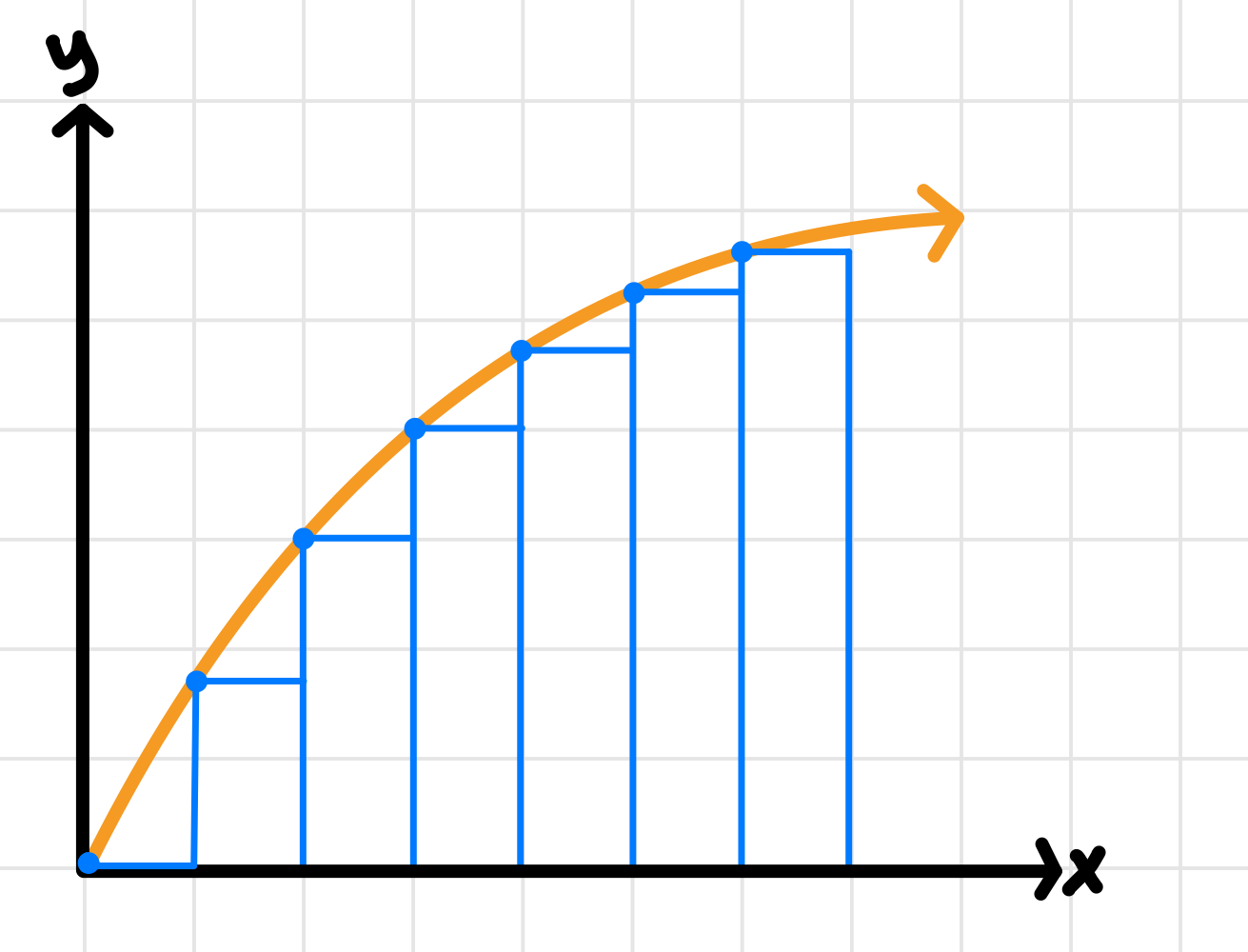
Image courtesy of Emery
We can see that this isn’t exact, but that our approximation improves if we use more and more rectangles:
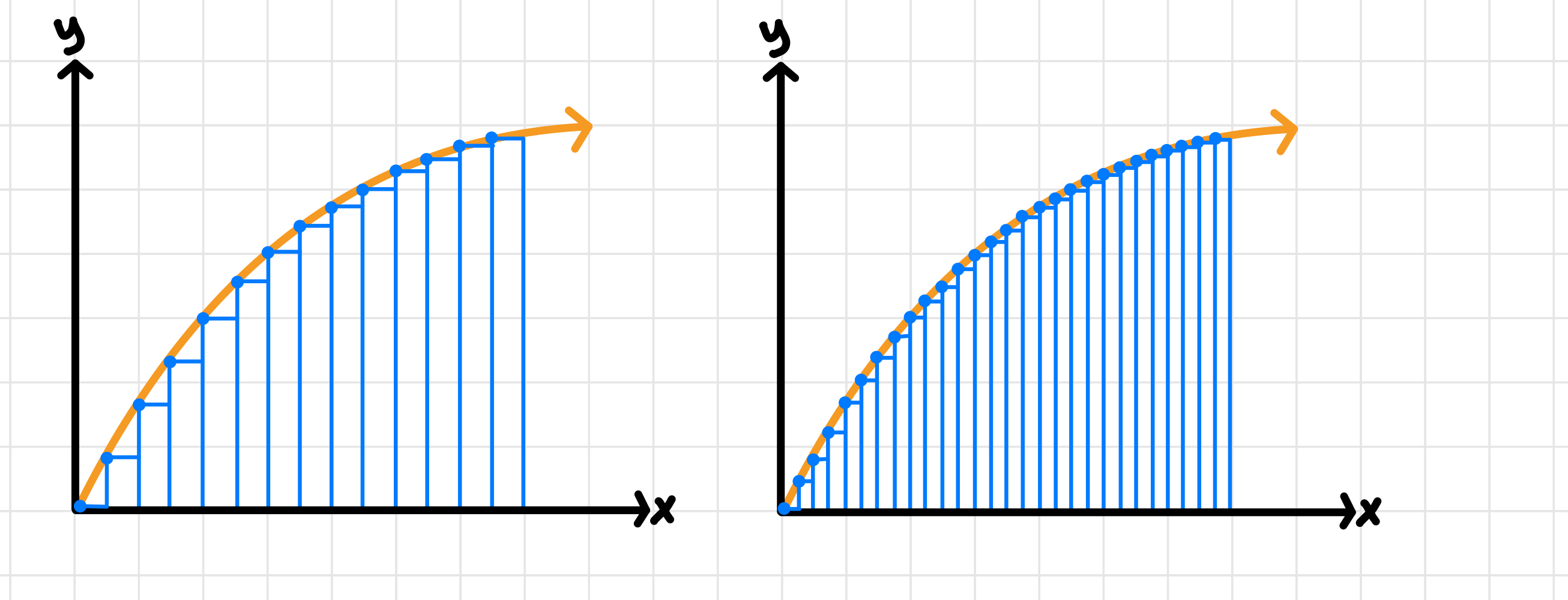
Image courtesy of Emery
The use of these rectangles to approximate the area under the curve is called a Riemann sum. There are four main Riemann sums:
- Left Riemann Sum
- Right Riemann Sum
- Midpoint Riemann Sum
- Trapezoidal Sum
Now, let’s get into each of these in detail!
↔️ Left and Right Riemann Sum
There are two basic types of Riemann sums, called “left endpoint” and “right endpoint.” Here is an example of the same curve with a left Riemann sum, versus one with a right Riemann sum:

Image courtesy of Emery
You can see that the left and right refer to which points we use to determine the height of our rectangles. Left Riemann sums touch the curve with their top left corners, and right Riemann sums touch the curve with their top right corners.
➗ Subdivisions
Another thing that we can vary when deciding to take a Riemann sum is the width of our base. Our base length can either be uniform or non-uniform, as illustrated here:
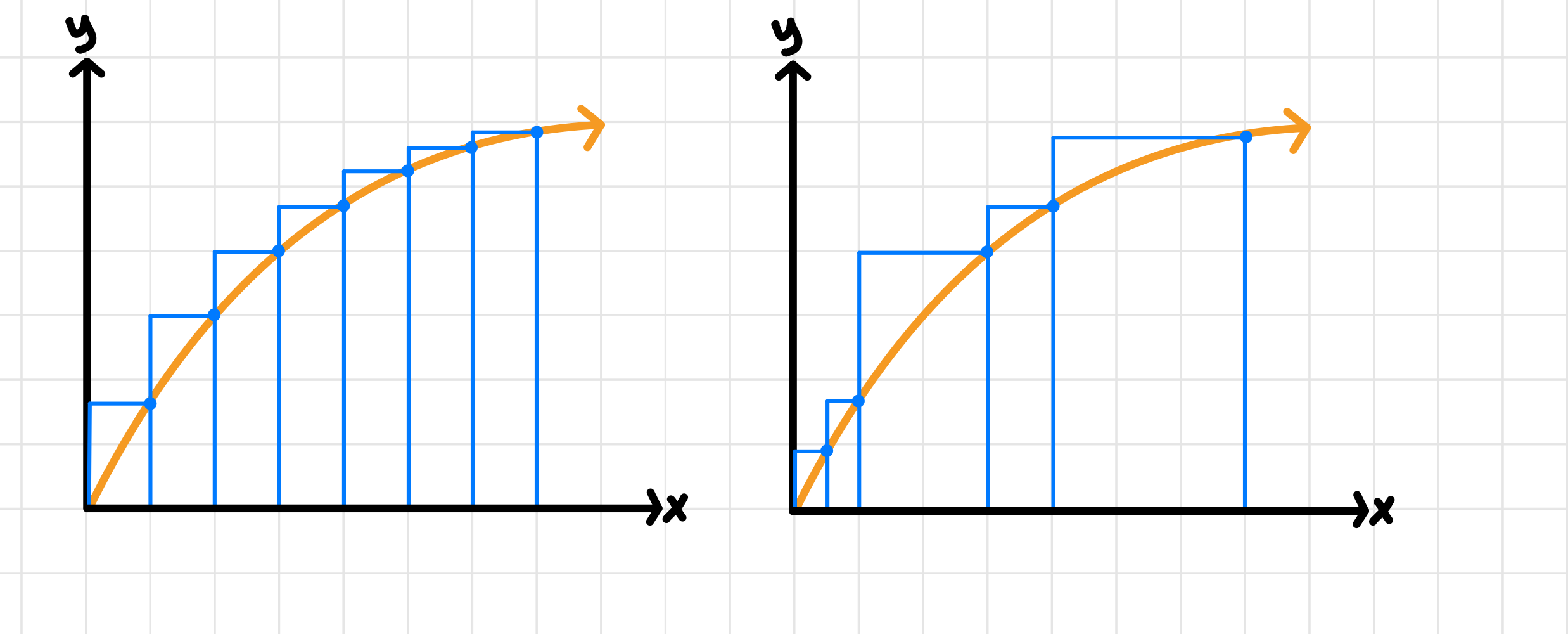
Image courtesy of Emery
The base lengths formed by dividing up the total interval are called “subdivisions.”
🤔 Overestimating vs Underestimating
We know that a Riemann sum isn’t a perfect calculation of our area under the curve, but are we overestimating or underestimating when we use one? Try these problems and then fill in the blanks to see if you can figure out the pattern!
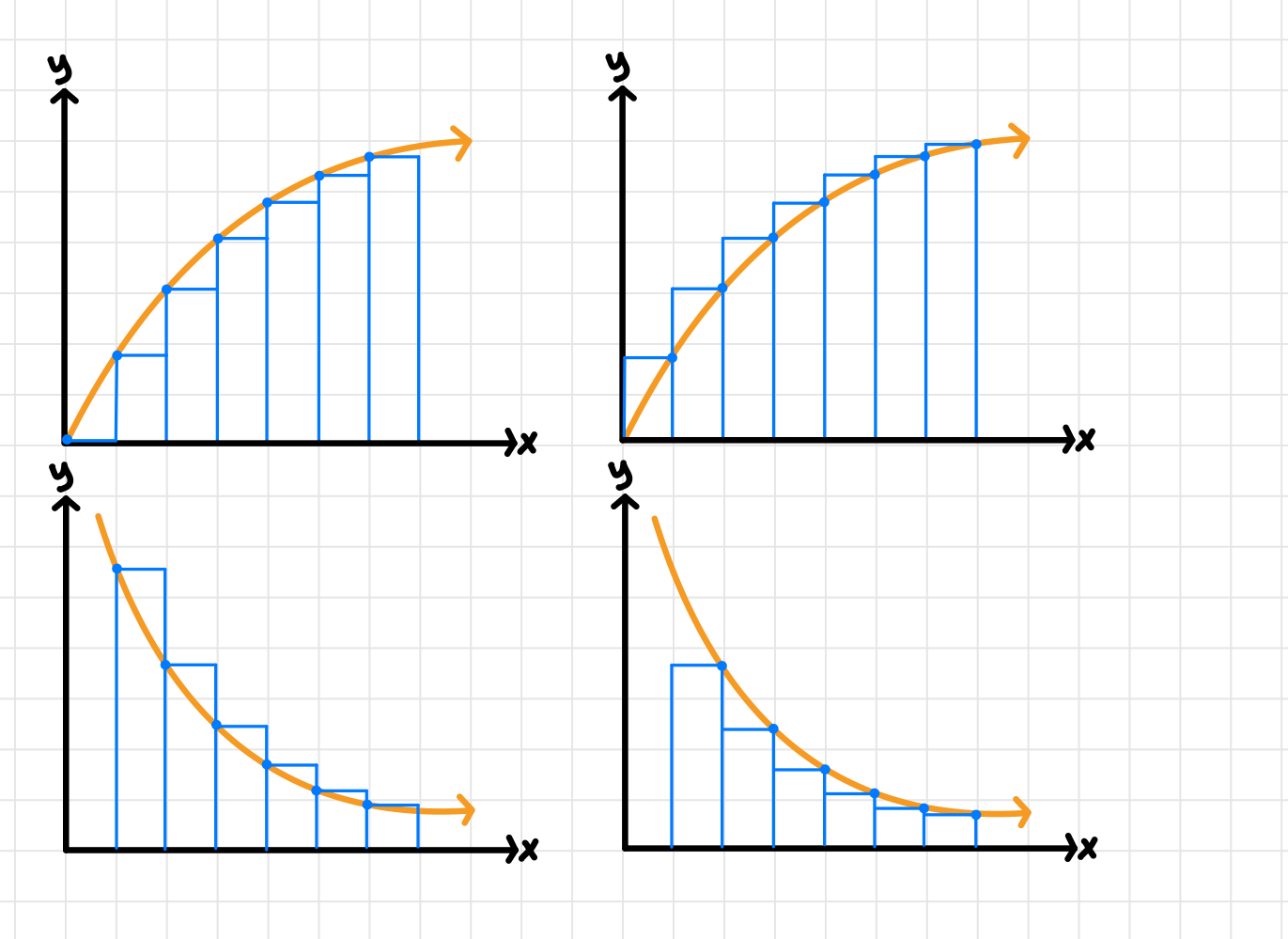
Image courtesy of Emery
Fill in the Blanks! 🧠
- A left Riemann sum ________when a function is ________.
- A right Riemann sum ________when a function is ________.
- A left Riemann sum ________when a function is ________.
- A right Riemann sum ________when a function is ________.
⚡ Answer Key:
If you haven’t already guessed the pattern, here are the rules:
- A left Riemann sum underestimates when a function is increasing 📈
- A right Riemann sum overestimates when a function is increasing 📈
- A left Riemann sum overestimates when a function is decreasing 📉
- A right Riemann sum underestimates when a function is decreasing 📉
Now that we know which types of Riemann sums make which types of errors in their estimations, how might we make our approximation more accurate?
📐 Trapezoidal and Midpoint Riemann Sums
If you guessed by averaging the two estimations, you’d be correct! We can do this in one of two ways.
📐 Trapezoidal Riemann Sum
If you’ve already calculated the left and right Riemann sum for a graph, you can simply take their average. But, there’s an even faster way to do this, using another simple geometric shape—the trapezoid! Instead of finding just the left or right endpoints, we mark every point over the interval we’re interested in. Then, we connect pairs of points together:

Image courtesy of Emery
This creates trapezoids! Instead of using the area formula for a rectangle, we now take the average of the two side lengths and multiple them by the base, using this formula:
📍 Midpoint Riemann Sum
Midpoint Riemann sums have the same goal as trapezoidal Riemann sums—to minimize the amount of error. They accomplish this by using the middle point of the rectangle as its height, as illustrated here:
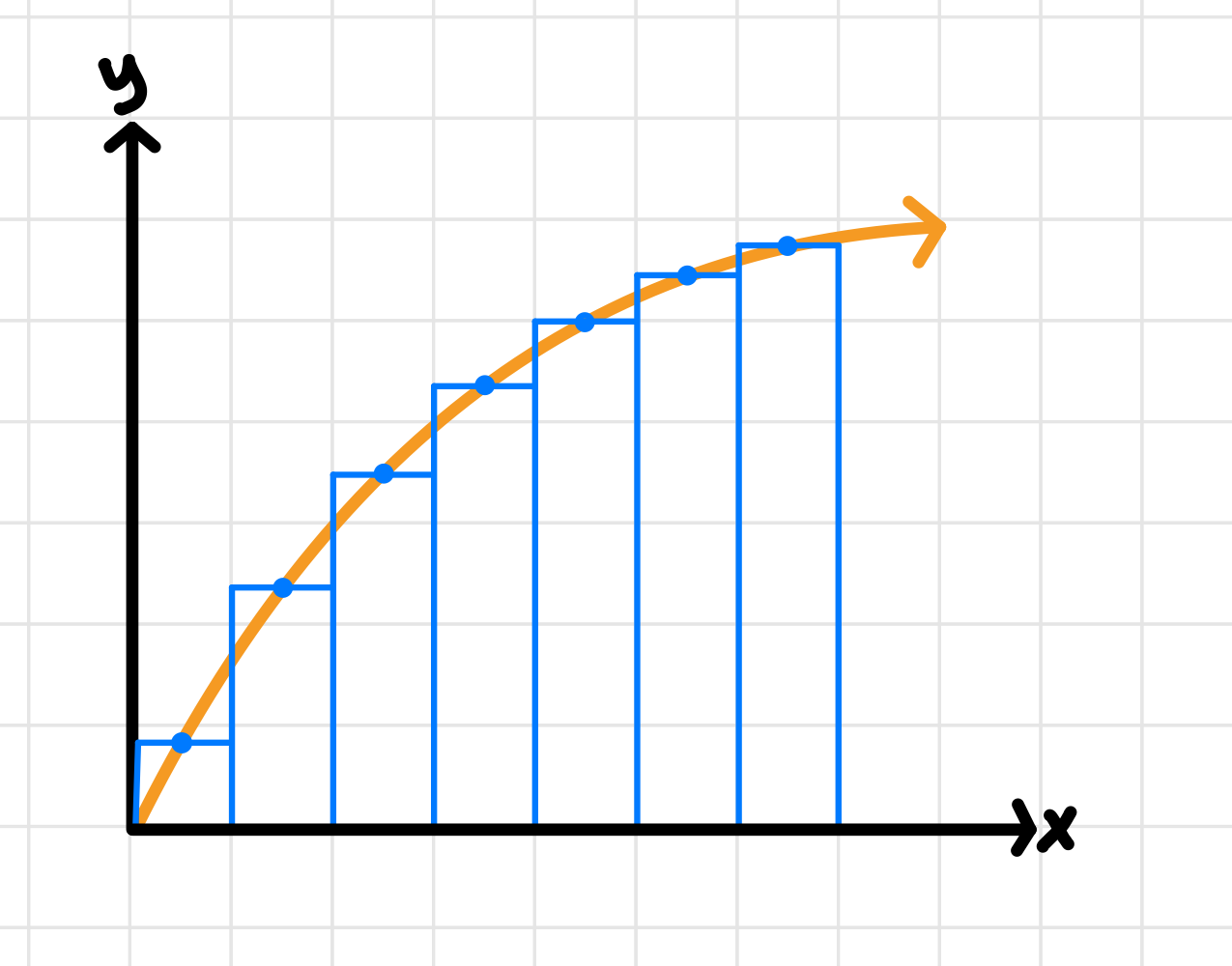
Image courtesy of Emery
🤔 Overestimating vs Underestimating
Just like left and right Riemann sums, the trapezoidal and midpoint Riemann sums may be an over- or underestimation depending on the type of graph.
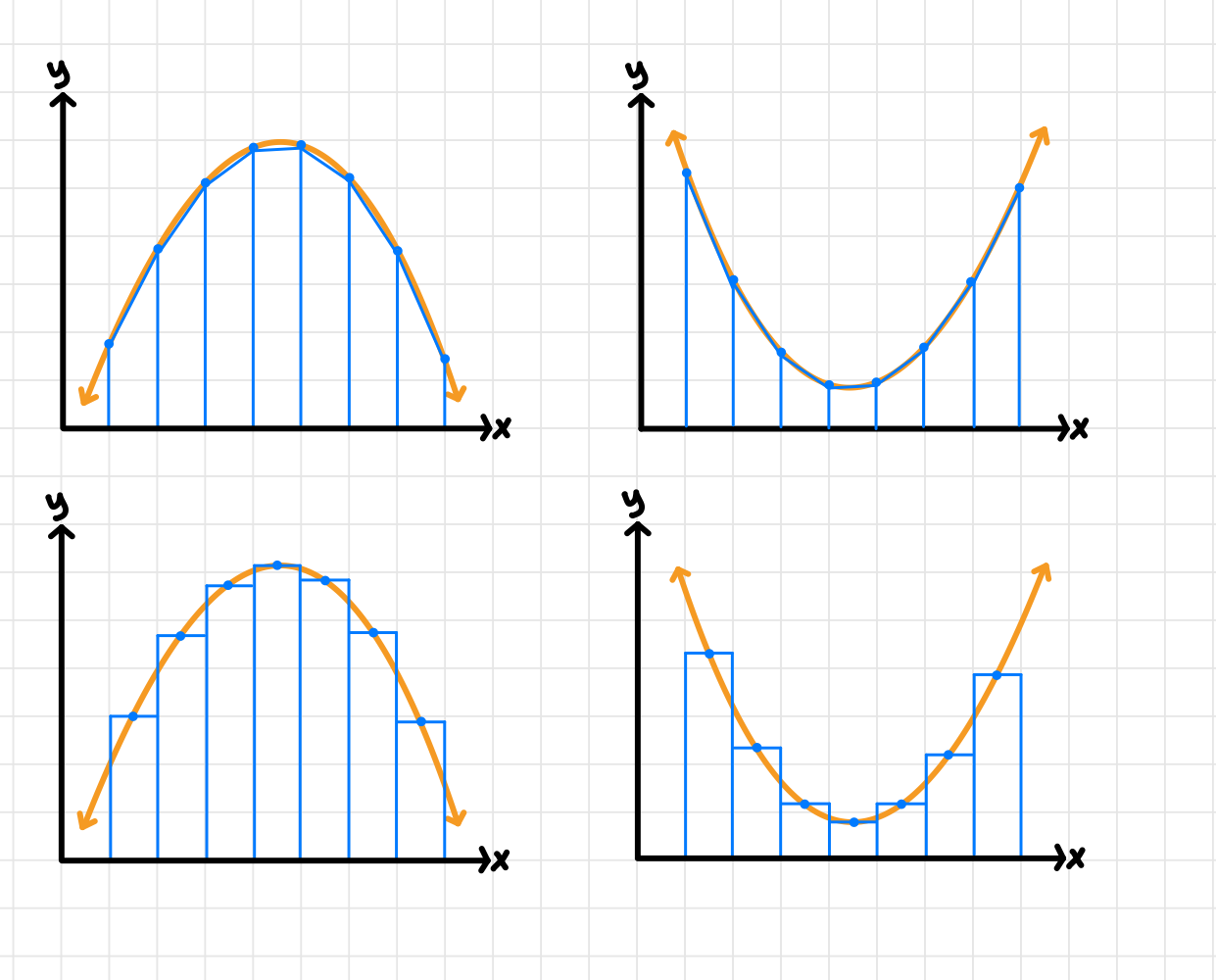
Image courtesy of Emery
Be familiar with the following:
- A trapezoidal Riemann sum underestimates when a function is concave down.
- A trapezoidal Riemann sum overestimates when a function is concave up.
- A midpoint Riemann sum underestimates when a function is concave up.
- A midpoint Riemann sum overestimates when a function is concave down.
🔢 Numerical Riemann Sums
Sometimes we’re not given a graph to base our estimates on! Let’s work through a sample problem to learn how to approach these types of problems.
Given the function , find and over the interval [0,4].
The very first thing you should do in this type of problem is draw a graph!
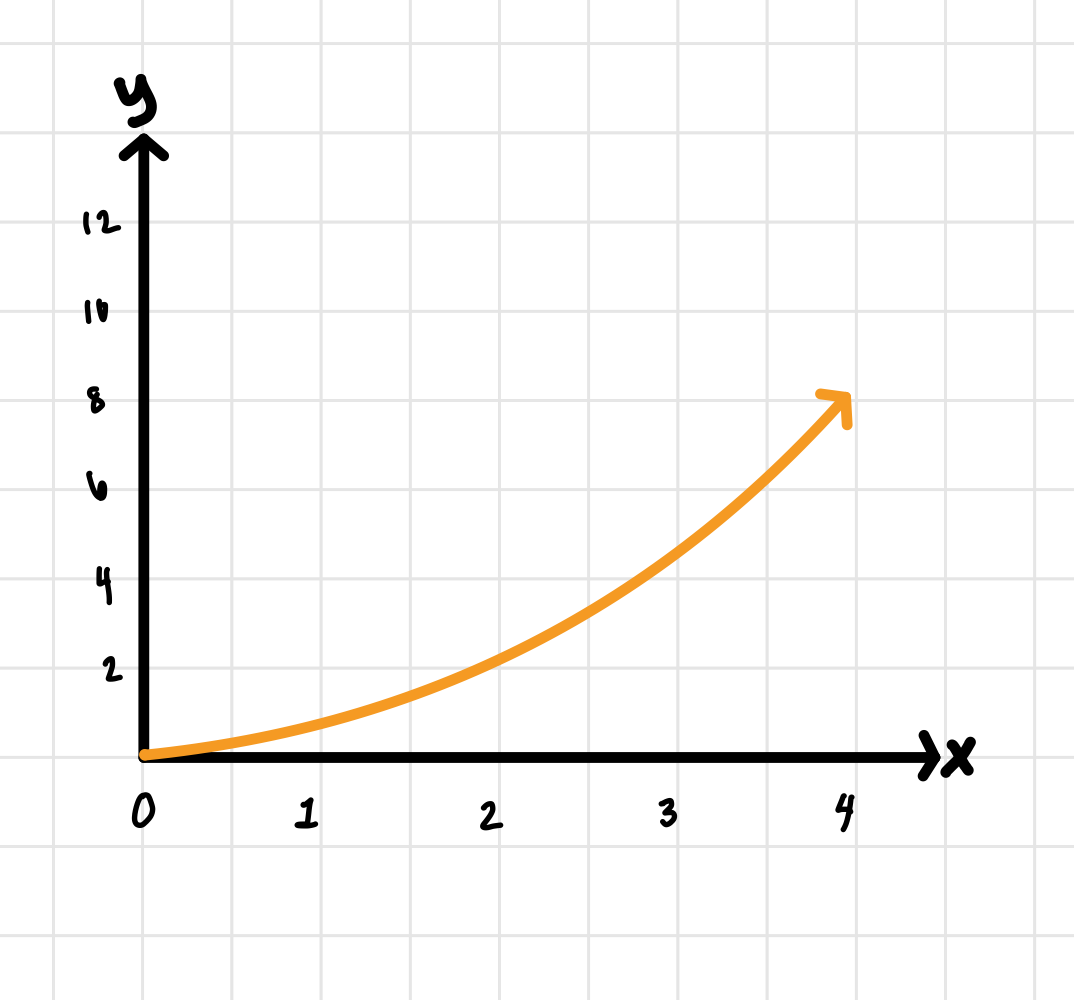
Image courtesy of Emery
Then, pick one of the Riemann sums to calculate. We’re going to solve for and first.
First, figure out how wide each rectangle will be by dividing the total interval by the number of subdivisions we want:
Then, draw our rectangles on the graph for each type of endpoint:
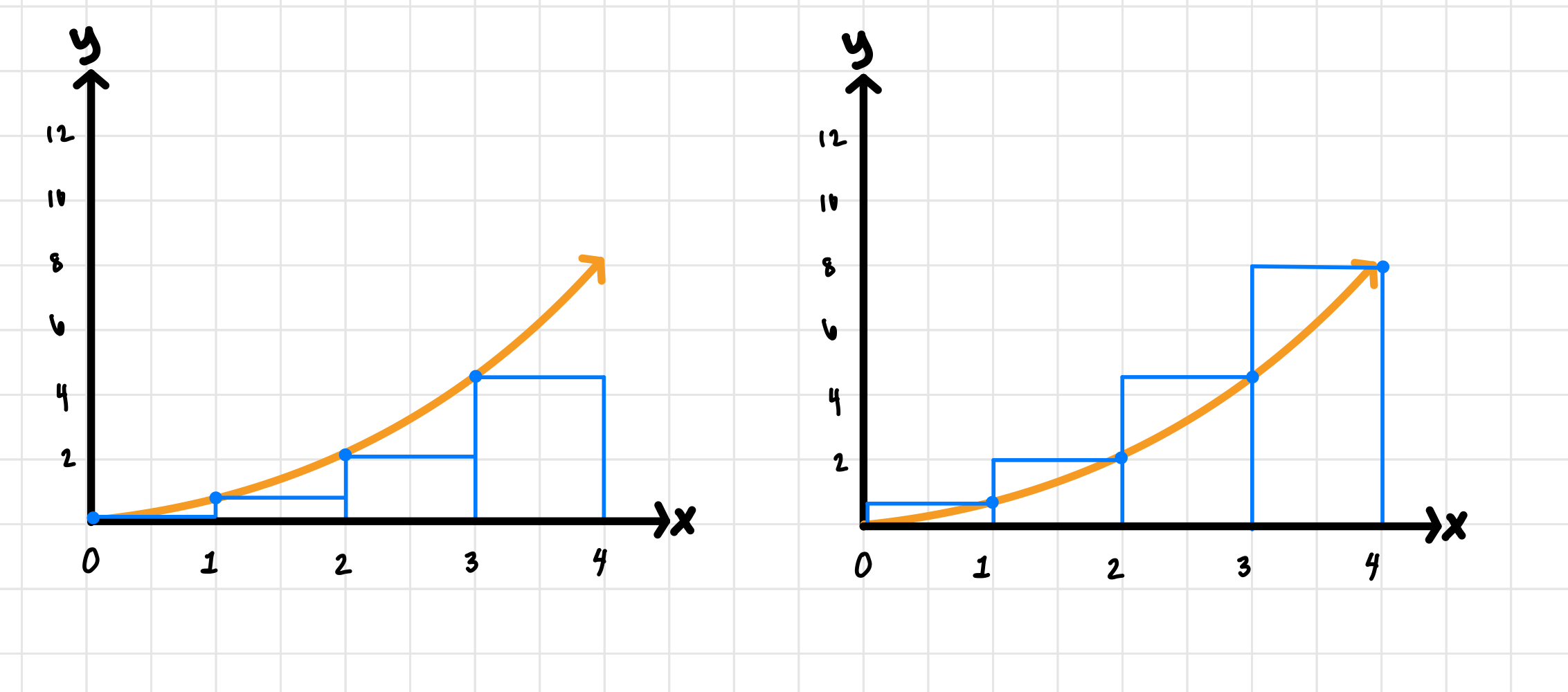
Image courtesy of Emery
We can also make a table of values from the graph:
| x | y (height) |
| 0 | 0 |
| 1 | 0.5 |
| 2 | 2 |
| 3 | 4.5 |
| 4 | 8 |
Based on our graphs, to find we need to use the left endpoints, which are . Since our base width is 1, we can just sum their values. Thus,
Let’s do the same thing for , using :
Now on to !
We know that there will be four trapezoids since we are using the same number of subdivisions. We can draw it like this:
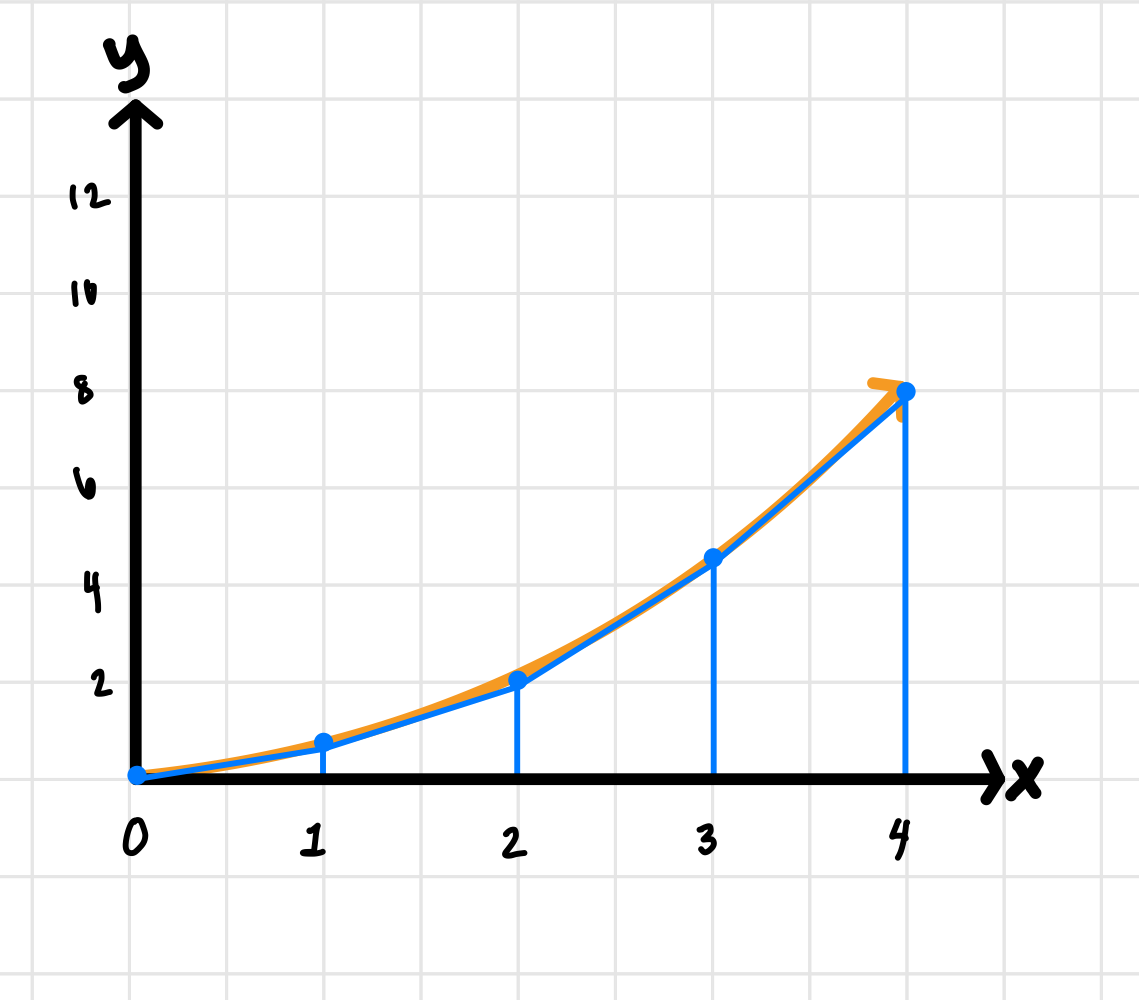
Image courtesy of Emery
We can also use the same table of values from the first part of the problem to find our values for a and b.
| x | y (height) |
| 0 | 0 |
| 1 | 0.5 |
| 2 | 2 |
| 3 | 4.5 |
| 4 | 8 |
Let’s plug these values into our equation to find the area of our first trapezoid:
We can do this for all four trapezoids and add them up to get our total area:
Finally, let’s find , starting by drawing our rectangles onto the graph:
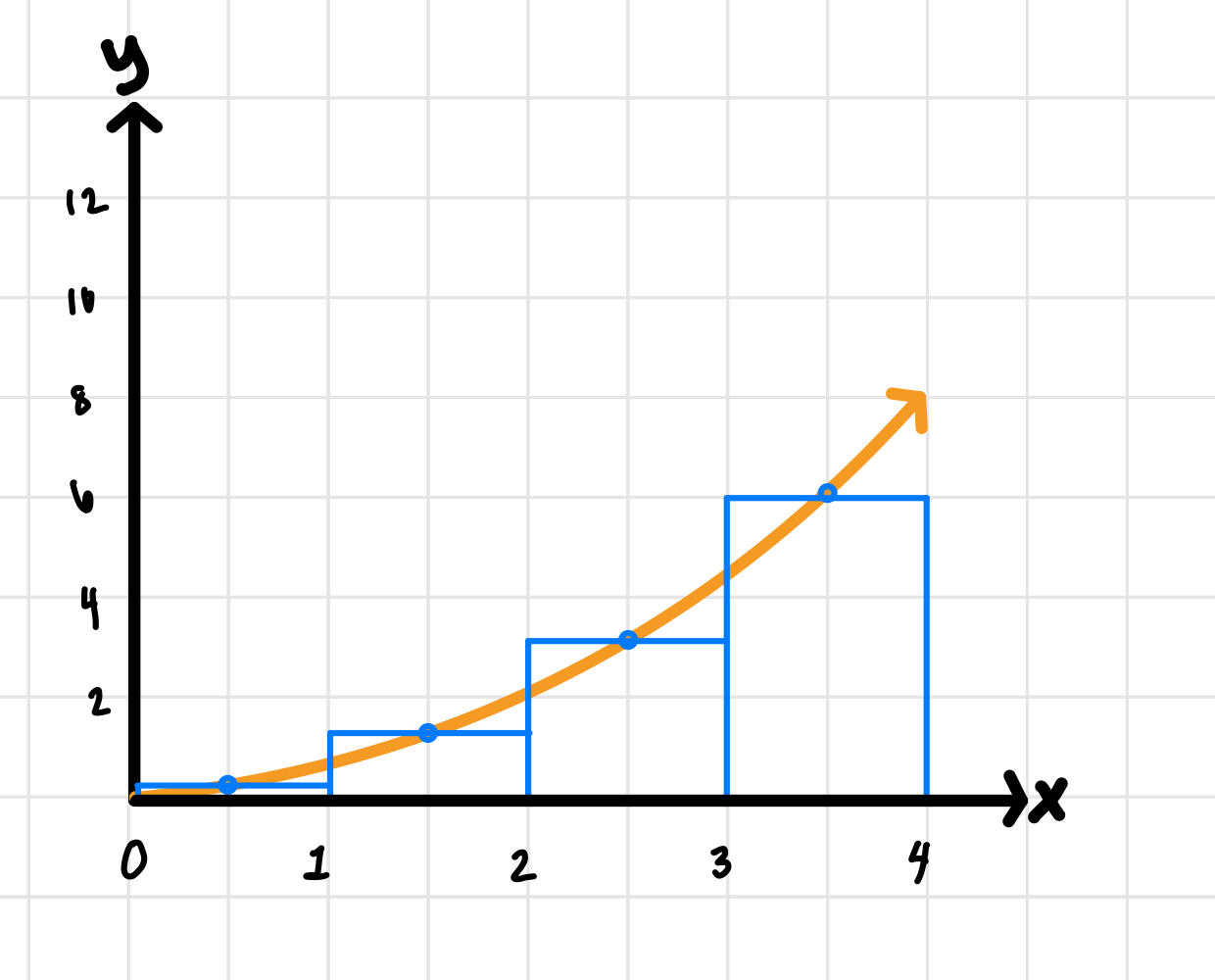
Image courtesy of Emery
First, we can plug in our x-values from the graph to find the height of each rectangle:
| x | y (height) |
| 0.5 | 0.125 |
| 1.5 | 1.125 |
| 2.5 | 3.125 |
| 3.5 | 6.125 |
Since our the width of each base is just 1, we can simply sum the four values to get our area under the curve estimated by :
Bonus Question: Are and overestimates or underestimates?
Solution: is an overestimate and is an underestimate, which means the true area under the curve lies somewhere between 10.5 and 11!
📝 Practice Problems and Solutions
Now take some time to practice these on your own!
❓Questions
- Given the function over the interval [1, 5], calculate the Riemann sum with using the right endpoints of each subinterval.
- A function is defined over the interval [0, 2]. Compute the left Riemann sum with for this function.
- Given the function over the interval [2, 8], find and .
✏️ Solutions
Problem 1 Solution****
First, let’s graph this function over the given interval:
Image courtesy of Emery
Then, let’s figure out what the width of our rectangles will be and graph with the right endpoints: .
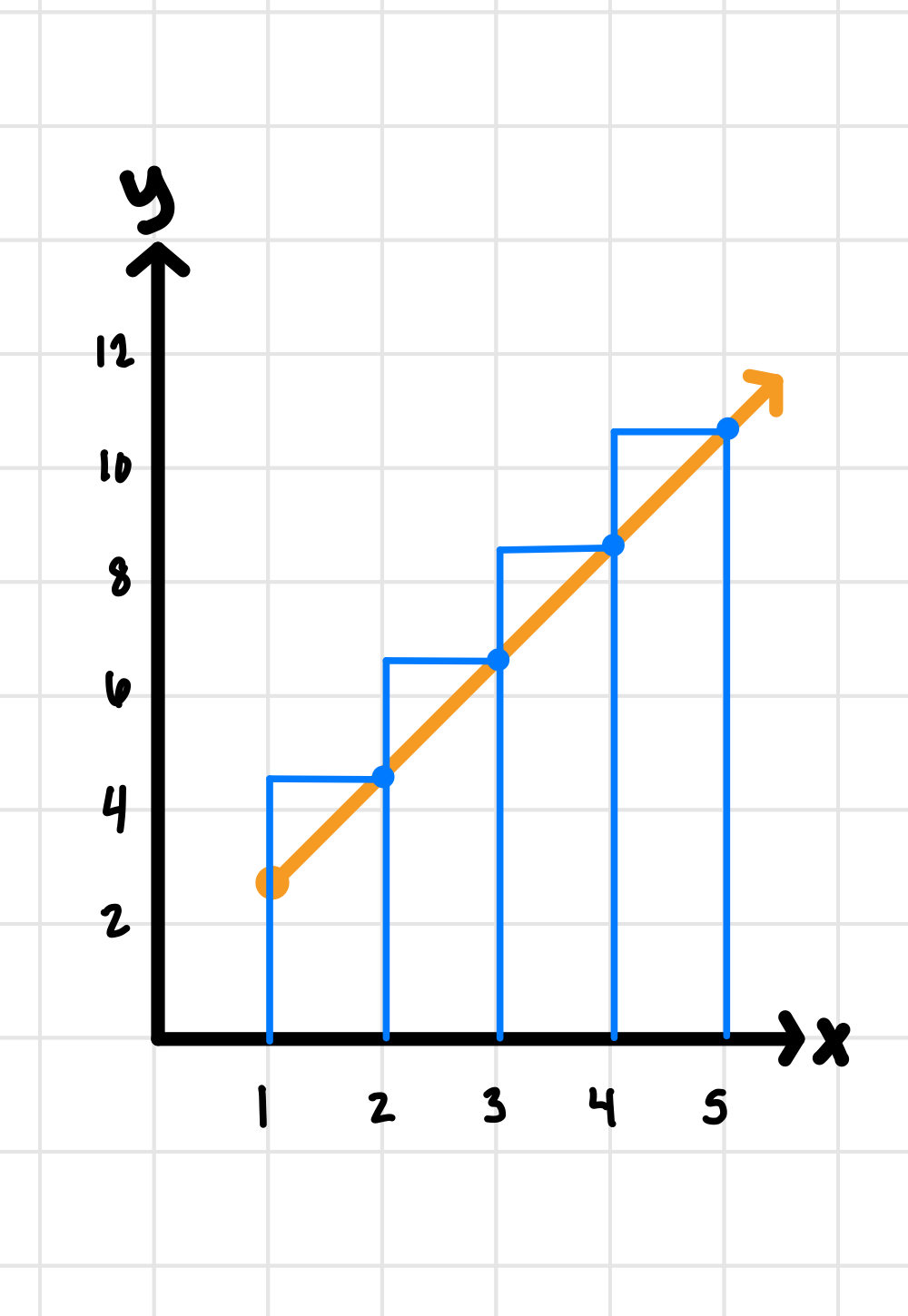
Image courtesy of Emery
Now, let’s find their heights numerically:
| x-value | y (height) |
| 2 | 5 |
| 3 | 7 |
| 4 | 9 |
| 5 | 11 |
Now, let’s solve by summing the areas of each rectangle:
Problem 2 Solution****
First, let’s graph this function over the given interval:
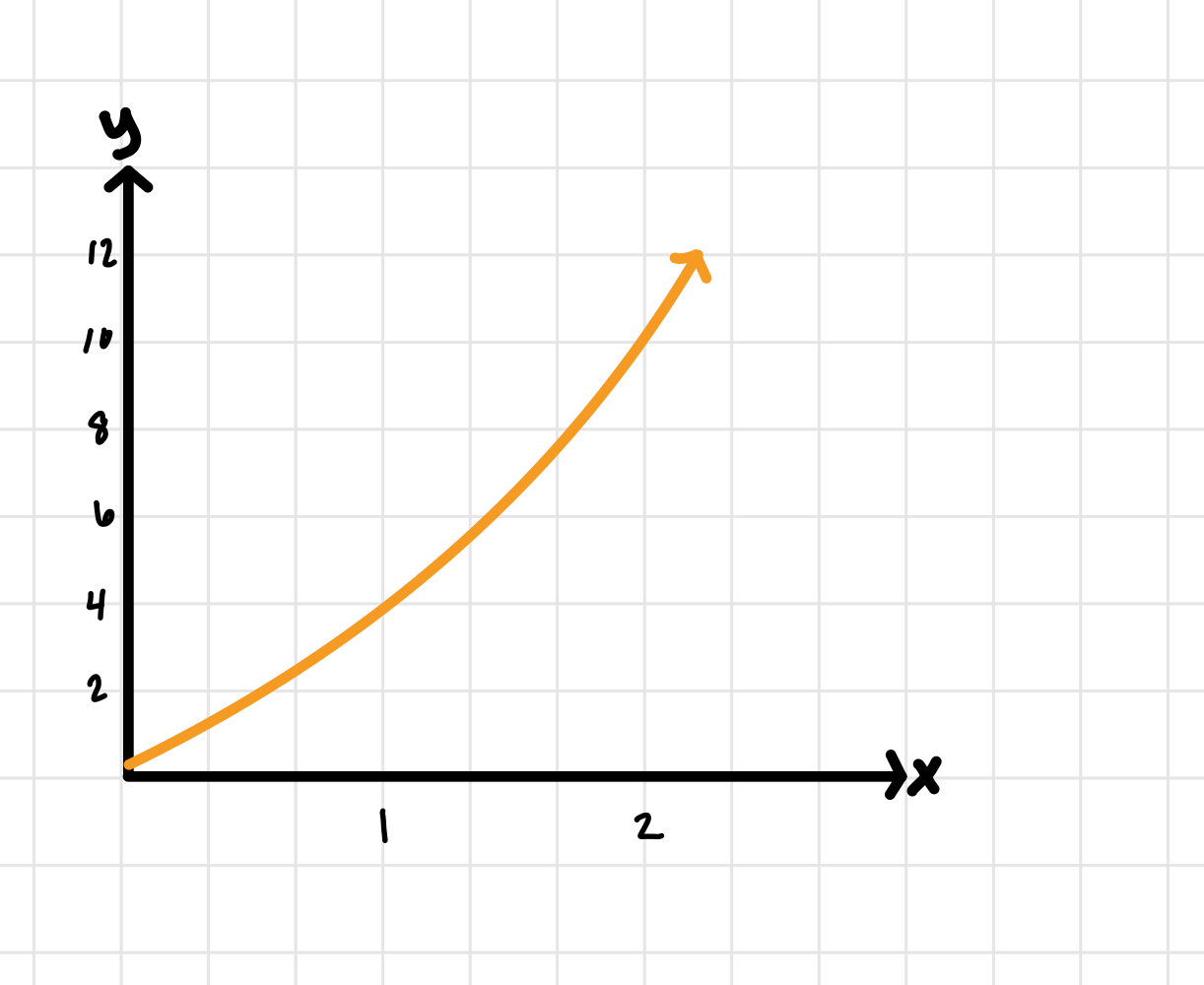
Image courtesy of Emery
Then, let’s figure out the width of our rectangles and graph with the left endpoints:

Image courtesy of Emery
Now, let’s find their heights numerically:
| x-value | y (height) |
| 0 | 0 |
| 1/3 | 10/9 |
| 2/3 | 22/9 |
| 1 | 4 |
| 4/3 | 52/9 |
| 5/3 | 70/9 |
Now, let’s solve by summing the areas of each rectangle:
We can rewrite this by factoring out our base length like so:
Problem 3 Solution****
First, let’s graph the function over the given interval:

Image courtesy of Emery
Then, let’s figure out the width of our rectangles and graph with the trapezoids:

Image courtesy of Emery
Let’s start by solving for by creating a table of values:
| x-value | y (height) |
| 2 | 8 |
| 2.5 | 14.75 |
| 3 | 23 |
| 3.5 | 32.75 |
| 4 | 44 |
| 4.5 | 56.75 |
| 5 | 71 |
| 5.5 | 86.75 |
| 6 | 104 |
| 6.5 | 122.75 |
| 7 | 143 |
| 7.5 | 164.75 |
| 8 | 188 |
Now, let’s plug it into our equation:
And simplify!
Let’s do the same with midpoints:
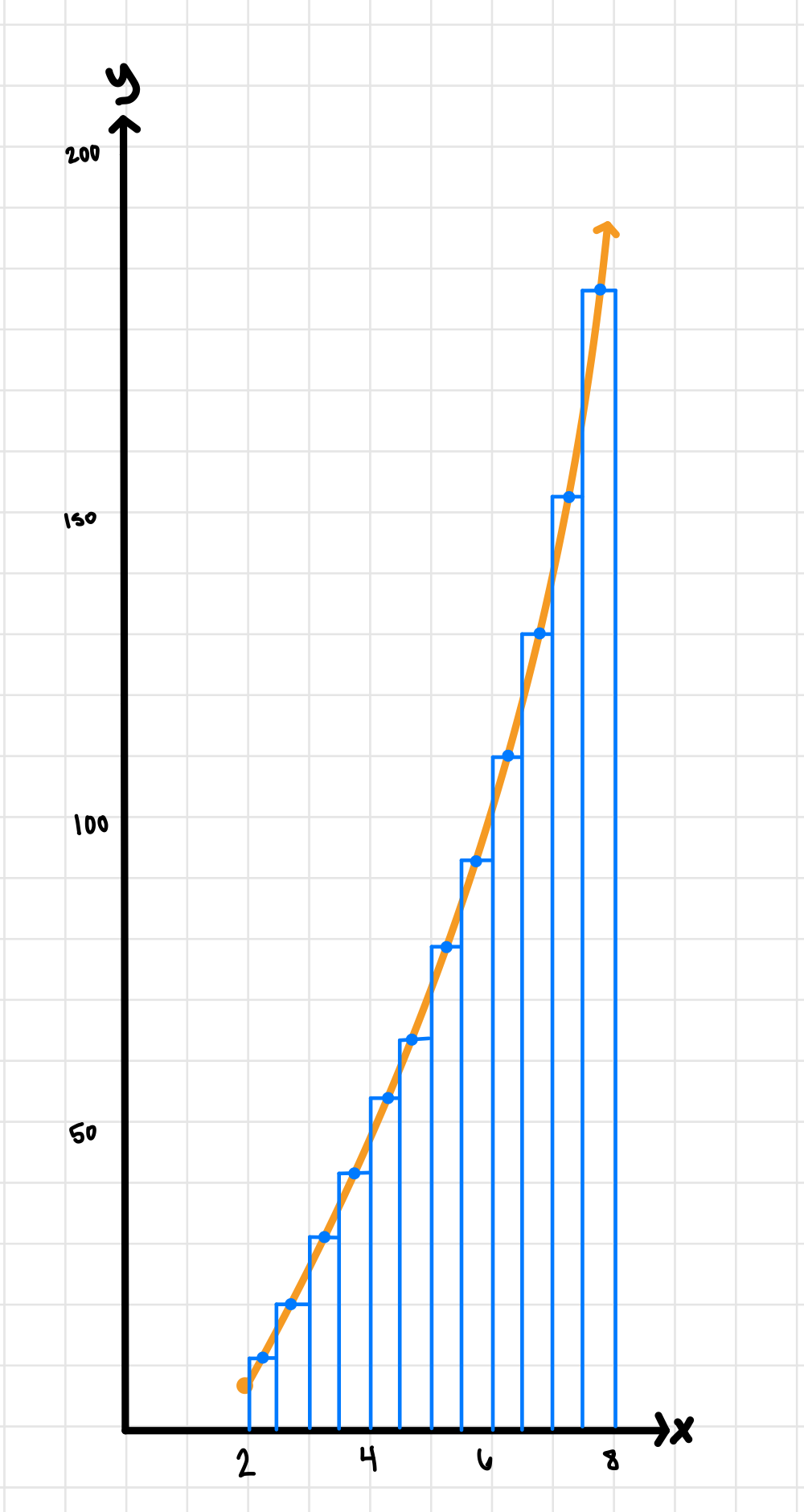
Image courtesy of Emery
| x-value | y (height) |
| 2.25 | 11.1875 |
| 2.75 | 18.6875 |
| 3.25 | 27.6875 |
| 3.75 | 38.1875 |
| 4.25 | 50.1875 |
| 4.75 | 63.6875 |
| 5.25 | 78.6875 |
| 5.75 | 95.1875 |
| 6.25 | 113.1875 |
| 6.75 | 132.6875 |
| 7.25 | 153.6875 |
| 7.75 | 176.1875 |
Now, let’s plug in and solve:
🌟 Closing
Here are the key takeaways you should now understand about Riemann sums:
- What a left, right, trapezoidal, or midpoint Riemann sum is and…
- How to calculate their values numerically
- When they are overestimates or underestimates
- How to determine the width of rectangles or trapezoids
- How to depict Riemann sums graphically
Best of luck! 🍀
<< Hide Menu
6.2 Approximating Areas with Riemann Sums
1 min read•june 18, 2024
Emery
Emery
6.2 Approximating Areas with Riemann Sums
Welcome back to AP Calc with Fiveable! In the last guide, we explored accumulations of change and thought about how to compute them. Here, we’ll take a deep dive into Riemann sums, a method for approximating the area under the curve to find the accumulation of change.
📶 Graphical Riemann Sums
As we delve into integral calculus, our goal has shifted from computing the instantaneous rate of change to computing the area under the curve. Riemann sums are a useful tool for approximating this. Take a look at this graph:

Image courtesy of Emery
You would have a hard time computing this geometrically. But, we can approximate it using familiar shapes, like this:

Image courtesy of Emery
We can see that this isn’t exact, but that our approximation improves if we use more and more rectangles:

Image courtesy of Emery
The use of these rectangles to approximate the area under the curve is called a Riemann sum. There are four main Riemann sums:
- Left Riemann Sum
- Right Riemann Sum
- Midpoint Riemann Sum
- Trapezoidal Sum
Now, let’s get into each of these in detail!
↔️ Left and Right Riemann Sum
There are two basic types of Riemann sums, called “left endpoint” and “right endpoint.” Here is an example of the same curve with a left Riemann sum, versus one with a right Riemann sum:

Image courtesy of Emery
You can see that the left and right refer to which points we use to determine the height of our rectangles. Left Riemann sums touch the curve with their top left corners, and right Riemann sums touch the curve with their top right corners.
➗ Subdivisions
Another thing that we can vary when deciding to take a Riemann sum is the width of our base. Our base length can either be uniform or non-uniform, as illustrated here:

Image courtesy of Emery
The base lengths formed by dividing up the total interval are called “subdivisions.”
🤔 Overestimating vs Underestimating
We know that a Riemann sum isn’t a perfect calculation of our area under the curve, but are we overestimating or underestimating when we use one? Try these problems and then fill in the blanks to see if you can figure out the pattern!

Image courtesy of Emery
Fill in the Blanks! 🧠
- A left Riemann sum ________when a function is ________.
- A right Riemann sum ________when a function is ________.
- A left Riemann sum ________when a function is ________.
- A right Riemann sum ________when a function is ________.
⚡ Answer Key:
If you haven’t already guessed the pattern, here are the rules:
- A left Riemann sum underestimates when a function is increasing 📈
- A right Riemann sum overestimates when a function is increasing 📈
- A left Riemann sum overestimates when a function is decreasing 📉
- A right Riemann sum underestimates when a function is decreasing 📉
Now that we know which types of Riemann sums make which types of errors in their estimations, how might we make our approximation more accurate?
📐 Trapezoidal and Midpoint Riemann Sums
If you guessed by averaging the two estimations, you’d be correct! We can do this in one of two ways.
📐 Trapezoidal Riemann Sum
If you’ve already calculated the left and right Riemann sum for a graph, you can simply take their average. But, there’s an even faster way to do this, using another simple geometric shape—the trapezoid! Instead of finding just the left or right endpoints, we mark every point over the interval we’re interested in. Then, we connect pairs of points together:

Image courtesy of Emery
This creates trapezoids! Instead of using the area formula for a rectangle, we now take the average of the two side lengths and multiple them by the base, using this formula:
📍 Midpoint Riemann Sum
Midpoint Riemann sums have the same goal as trapezoidal Riemann sums—to minimize the amount of error. They accomplish this by using the middle point of the rectangle as its height, as illustrated here:

Image courtesy of Emery
🤔 Overestimating vs Underestimating
Just like left and right Riemann sums, the trapezoidal and midpoint Riemann sums may be an over- or underestimation depending on the type of graph.

Image courtesy of Emery
Be familiar with the following:
- A trapezoidal Riemann sum underestimates when a function is concave down.
- A trapezoidal Riemann sum overestimates when a function is concave up.
- A midpoint Riemann sum underestimates when a function is concave up.
- A midpoint Riemann sum overestimates when a function is concave down.
🔢 Numerical Riemann Sums
Sometimes we’re not given a graph to base our estimates on! Let’s work through a sample problem to learn how to approach these types of problems.
Given the function , find and over the interval [0,4].
The very first thing you should do in this type of problem is draw a graph!

Image courtesy of Emery
Then, pick one of the Riemann sums to calculate. We’re going to solve for and first.
First, figure out how wide each rectangle will be by dividing the total interval by the number of subdivisions we want:
Then, draw our rectangles on the graph for each type of endpoint:
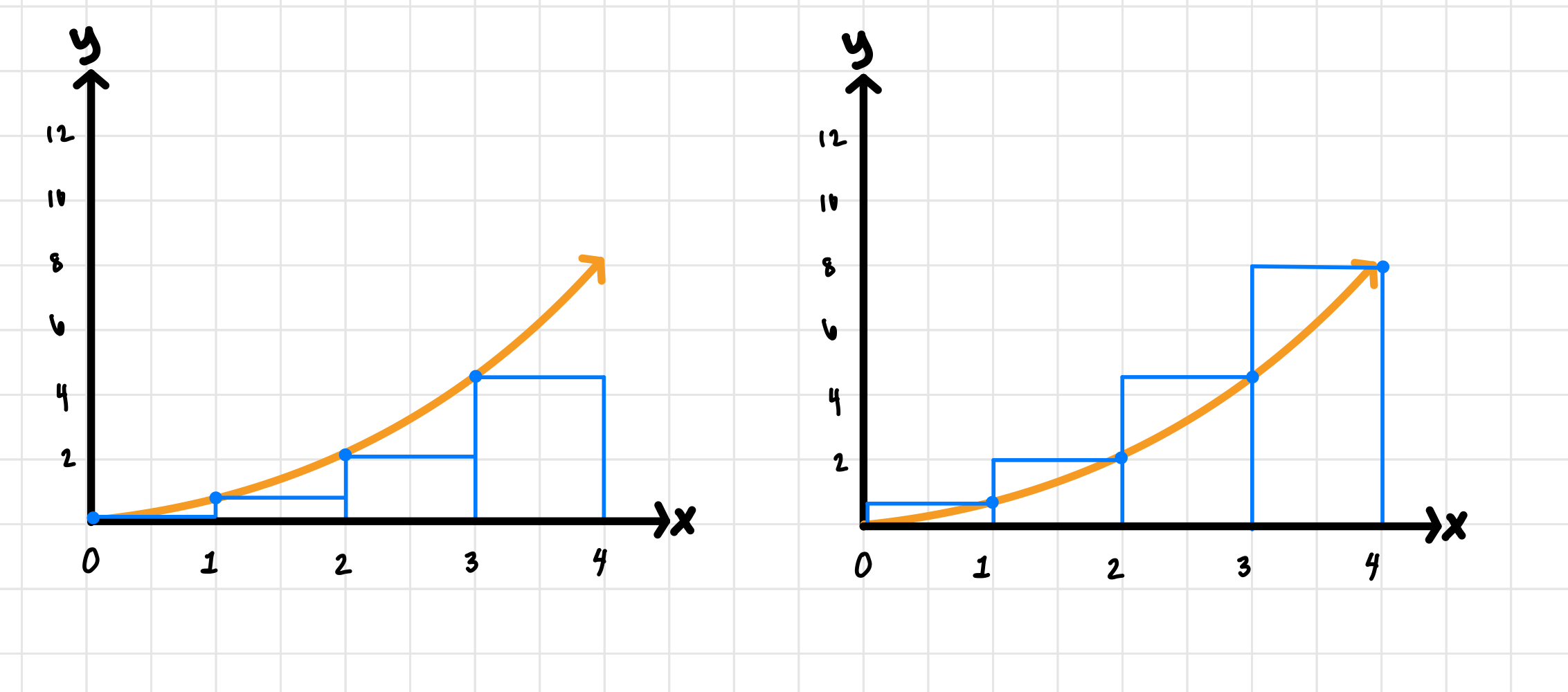
Image courtesy of Emery
We can also make a table of values from the graph:
| x | y (height) |
| 0 | 0 |
| 1 | 0.5 |
| 2 | 2 |
| 3 | 4.5 |
| 4 | 8 |
Based on our graphs, to find we need to use the left endpoints, which are . Since our base width is 1, we can just sum their values. Thus,
Let’s do the same thing for , using :
Now on to !
We know that there will be four trapezoids since we are using the same number of subdivisions. We can draw it like this:
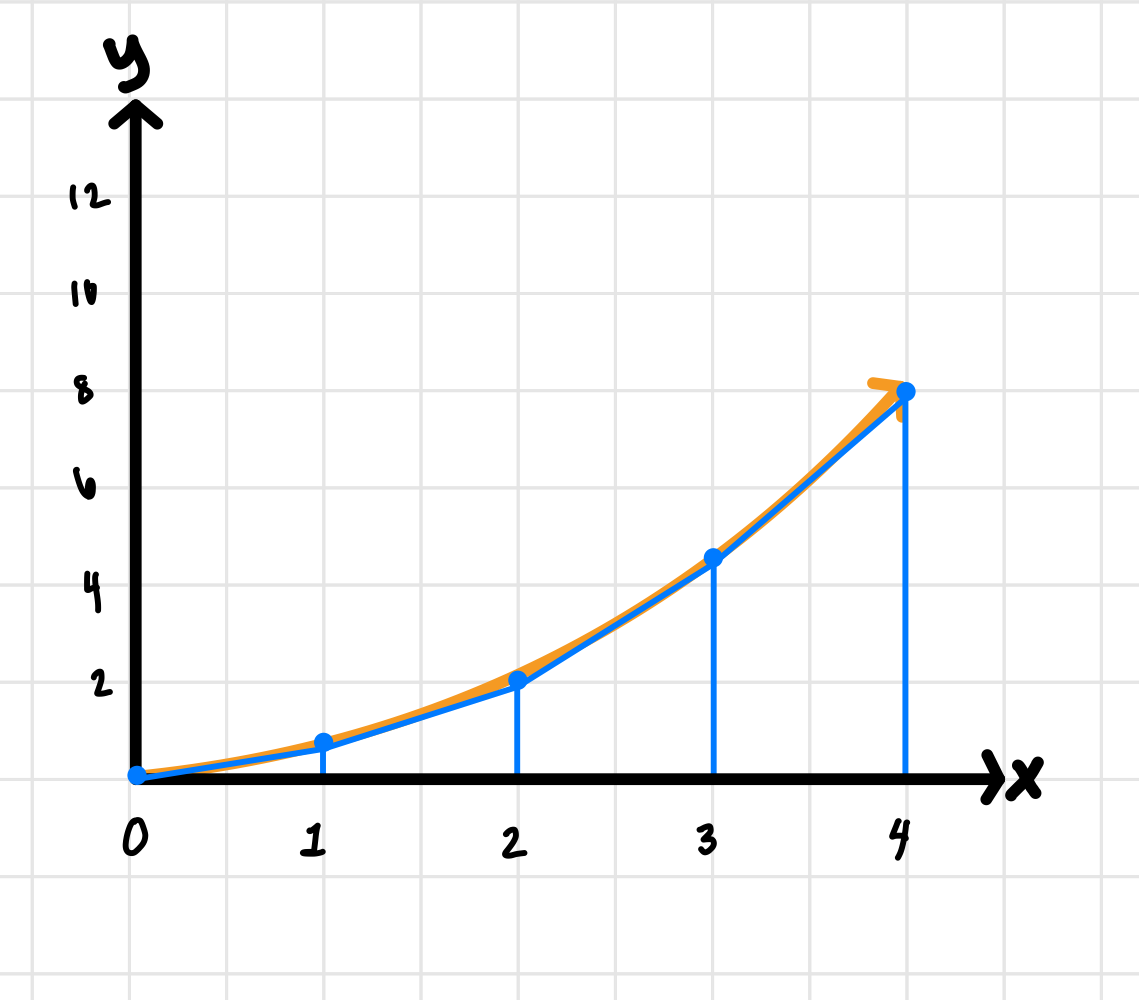
Image courtesy of Emery
We can also use the same table of values from the first part of the problem to find our values for a and b.
| x | y (height) |
| 0 | 0 |
| 1 | 0.5 |
| 2 | 2 |
| 3 | 4.5 |
| 4 | 8 |
Let’s plug these values into our equation to find the area of our first trapezoid:
We can do this for all four trapezoids and add them up to get our total area:
Finally, let’s find , starting by drawing our rectangles onto the graph:

Image courtesy of Emery
First, we can plug in our x-values from the graph to find the height of each rectangle:
| x | y (height) |
| 0.5 | 0.125 |
| 1.5 | 1.125 |
| 2.5 | 3.125 |
| 3.5 | 6.125 |
Since our the width of each base is just 1, we can simply sum the four values to get our area under the curve estimated by :
Bonus Question: Are and overestimates or underestimates?
Solution: is an overestimate and is an underestimate, which means the true area under the curve lies somewhere between 10.5 and 11!
📝 Practice Problems and Solutions
Now take some time to practice these on your own!
❓Questions
- Given the function over the interval [1, 5], calculate the Riemann sum with using the right endpoints of each subinterval.
- A function is defined over the interval [0, 2]. Compute the left Riemann sum with for this function.
- Given the function over the interval [2, 8], find and .
✏️ Solutions
Problem 1 Solution****
First, let’s graph this function over the given interval:

Image courtesy of Emery
Then, let’s figure out what the width of our rectangles will be and graph with the right endpoints: .

Image courtesy of Emery
Now, let’s find their heights numerically:
| x-value | y (height) |
| 2 | 5 |
| 3 | 7 |
| 4 | 9 |
| 5 | 11 |
Now, let’s solve by summing the areas of each rectangle:
Problem 2 Solution****
First, let’s graph this function over the given interval:
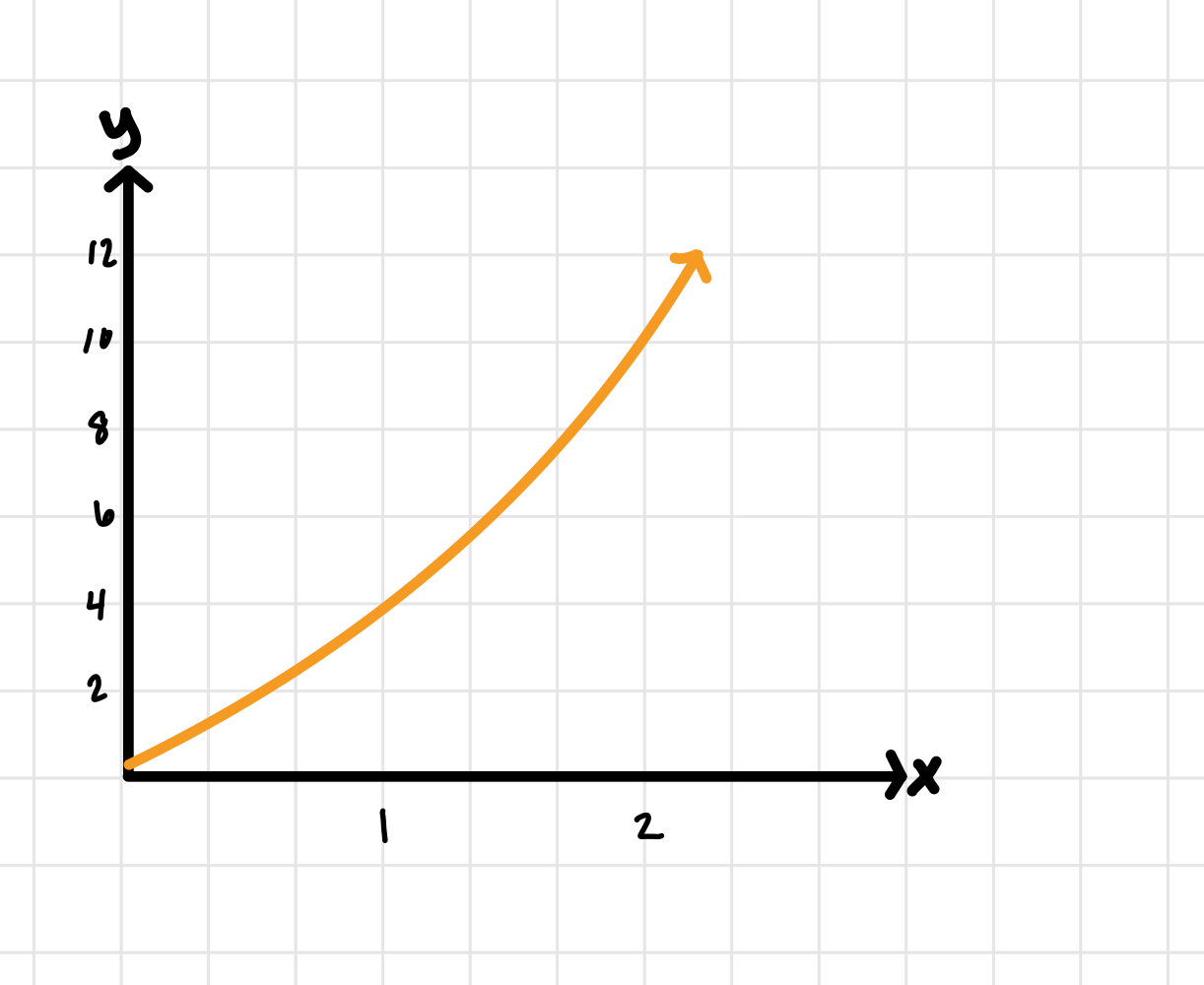
Image courtesy of Emery
Then, let’s figure out the width of our rectangles and graph with the left endpoints:

Image courtesy of Emery
Now, let’s find their heights numerically:
| x-value | y (height) |
| 0 | 0 |
| 1/3 | 10/9 |
| 2/3 | 22/9 |
| 1 | 4 |
| 4/3 | 52/9 |
| 5/3 | 70/9 |
Now, let’s solve by summing the areas of each rectangle:
We can rewrite this by factoring out our base length like so:
Problem 3 Solution****
First, let’s graph the function over the given interval:

Image courtesy of Emery
Then, let’s figure out the width of our rectangles and graph with the trapezoids:

Image courtesy of Emery
Let’s start by solving for by creating a table of values:
| x-value | y (height) |
| 2 | 8 |
| 2.5 | 14.75 |
| 3 | 23 |
| 3.5 | 32.75 |
| 4 | 44 |
| 4.5 | 56.75 |
| 5 | 71 |
| 5.5 | 86.75 |
| 6 | 104 |
| 6.5 | 122.75 |
| 7 | 143 |
| 7.5 | 164.75 |
| 8 | 188 |
Now, let’s plug it into our equation:
And simplify!
Let’s do the same with midpoints:

Image courtesy of Emery
| x-value | y (height) |
| 2.25 | 11.1875 |
| 2.75 | 18.6875 |
| 3.25 | 27.6875 |
| 3.75 | 38.1875 |
| 4.25 | 50.1875 |
| 4.75 | 63.6875 |
| 5.25 | 78.6875 |
| 5.75 | 95.1875 |
| 6.25 | 113.1875 |
| 6.75 | 132.6875 |
| 7.25 | 153.6875 |
| 7.75 | 176.1875 |
Now, let’s plug in and solve:
🌟 Closing
Here are the key takeaways you should now understand about Riemann sums:
- What a left, right, trapezoidal, or midpoint Riemann sum is and…
- How to calculate their values numerically
- When they are overestimates or underestimates
- How to determine the width of rectangles or trapezoids
- How to depict Riemann sums graphically
Best of luck! 🍀

© 2024 Fiveable Inc. All rights reserved.