Browse By Unit
5.8 Sketching Graphs of Functions and Their Derivatives
5 min read•june 18, 2024
Kashvi Panjolia
Kashvi Panjolia
5.8 My Combo
Previously you learned all about utilizing a function’s derivatives to find its increasing and decreasing intervals, relative and global extrema, concave up and concave down intervals, and more! Can we combine all this to form a complete image of a function’s graph? Yes, we can! Today, you’ll learn how to utilize all these tools in your toolbox to form an overall picture of a function.
📈 Sketching Graphs
Drawing the graphs of functions and their derivatives is very useful in determining key features of the function. From a graph, you can identify discontinuities, find critical points, and extrema, and discern many other important elements of a function.
There are seven steps to sketching a graph. This may seem like a lot, but once you break it down, you’ll get a hang of it! 🔎
- 〰️ Find the domain of the function and determine if there are any discontinuities.
- 🎯 Identify key features of the function, such as intercepts and symmetry.
- 💯 Find critical points.
- 📶 Determine where the function increases and decreases.
- 🤔 Find the extrema of the function.
- 🥈 An alternative to steps 4) and 5) is to use the Second Derivative Test to determine the extrema of the function.
- ✏️ Determine points of inflection and intervals of concavity.
And there we have it! An overview of what the entire function looks like! You can now use all these interesting points to sketch a graph of the function. 😄
🎨 Sketching Graphs Walkthrough
Now, let’s delve deeper into what each of these steps entails and sketch the following function!
〰️ Step 1) Find the domain and look for discontinuities.
A useful fact to memorize is that all polynomial functions have a domain consisting of all real numbers. Since we’re graphing a polynomial here, we know that the domain consists of all real numbers.
When looking for discontinuities, note if the function is rational or has any points where is not defined. Since there seem to be no points where is not defined, we can conclude that this function is continuous everywhere in its domain.
🎯 Step 2) Identify key features of the function, such as intercepts and symmetry.
First, let’s look for x-intercepts, where .
We can quickly do this by setting each factor equal to zero and solving for x.
And now, to set equal to 0.
This gives us two x-intercepts: and . The coordinates of these x-intercepts are and . Great! We got our first points we can plot.
Let’s now look for y-intercepts, where .
We have another point we can jot down to plot later! The coordinates of the y-intercept are .
Lastly, let’s look for symmetry. A function is symmetric with respect to a line if, when reflected across that line, the function looks the same as the original function. There are two types of symmetry a function may have:
- Even - the function is symmetrical across the y-axis. for all in the domain of the function.
- Odd - the function is symmetric about the origin. for all in the domain of the function.
If neither of these statements is true, the function has no symmetry. With our function, this is the case, so our function has no symmetry.

Image Courtesy of The Organic Chemistry Tutor
💯 Step 3) Find critical points.
If you recall from earlier sections of the unit, the first step of using a function’s derivative to determine its behavior involved finding critical points! These points occur when the function’s first derivative is equal to zero or is undefined.
The first derivative of our function is the following, using the product rule.
Setting this equal to zero and solving for x, we get and as the function’s critical points. We can use this information in the next step!
📶 Step 4) Determine where the function increases and decreases.
Using these critical points, we can determine the intervals where the function increases and decreases.
- ➕=📈 If the derivative of the function on the interval between two adjacent/nearest critical points is negative, then the function is decreasing on that interval.
- ➖=📉 If the derivative of the function is positive, then the function is increasing on that interval.
Please revisit our AP Calculus - 5.3 Determining Intervals on Which a Function Is Increasing or Decreasing guide for a more in-depth explanation!
Let’s evaluate the first derivative around each of our critical points:
| Interval | Verdict | ||
| is increasing | |||
| is decreasing | |||
| is increasing |
Whew! Now we know that is increasing between and and decreasing between .
🤔 Step 5) Find the extrema of the function.
Based on the information we discovered in the last step, we can easily apply the First Derivative Test to find the extrema of the function!
- ⬇️ The critical points where the function is decreasing on its left and increasing on its right are minimums.
- ⬆️ The critical points where the function is increasing on its left and decreasing on its right are maximums.
Visit our AP Calculus - 5.4 Using the First Derivative Test to Determine Relative (Local) Extrema guide if you need a refresher!
We know that to the left of , the function is increasing, and to the right of , the function is decreasing. Therefore, is a local maximum.
Vice versa is true for our critical point at . Since the function is decreasing to its left and increasing to its right, is a local minimum.
🥈 Alternative to Steps 4 & 5
An alternative to steps 4) and 5) is to use the Second Derivative Test to determine the extrema of the function. Recall that this test states that…
- If the second derivative of a function at a critical point is negative, then the function has a relative maximum at that point (and it’s concave down).
- If the second derivative of a function at a critical point is positive, then the function has a relative minimum at that point (and it’s concave up).
Please see our AP Calculus - 5.7 Using the Second Derivative Test to Determine Extrema guide.
✏️ Step 6) Determine points of inflection and concavity.
A function has a possible point of inflection if its second derivative is equal to zero at the point. To verify it is indeed a point of inflection, we must check to see if the function changes from concave up to concave down or vice versa (aka the second derivative changes from negative to positive or vice versa) on the two sides of the point.
For more information, revisit our AP Calculus - 5.6 Determining Concavity of Functions over Their Domains guide!
Here’s the second derivative of our function, .
Let’s find the possible point of inflection by setting this equal to 0.
Great! Now, we have to analyze the sign of the second derivative to see if this is a true point of inflection.
| Concavity | ||
| Concave down | ||
| Concave up |
Since the second derivative’s sign switches and the function’s concavity changes, is a point of inflection.
🎨 Putting it All Together!
Compiling all of the information we found, we know that:
- The function is continuous.
- We can plot , , and .
- is increasing between and .
- is decreasing between .
- is a local maximum.
- is a local minimum.
- Concavity changes at from concave down, to concave up.
And here we have it!
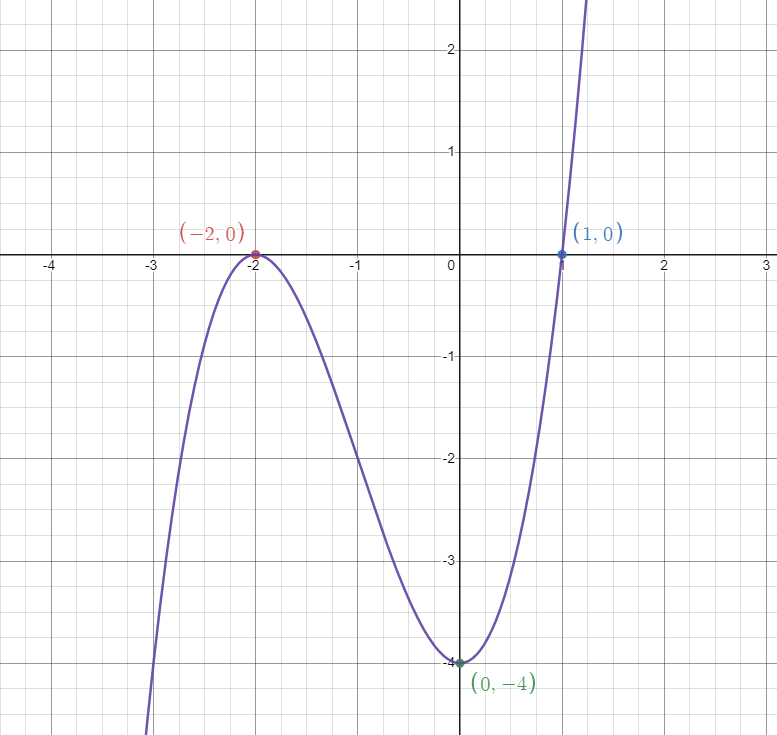
Image Created with Desmos.
You may not have needed all of the information we obtained, but having it all helps you double-check that you graphed correctly. Great work! 👏
📝 Sketching Graphs Practice
Try to sketch the following function on your own! What does the graph of look like?
Be sure to go through each step on your own before you scroll down further and see the answer!
✅ Sketching Graphs Question Solution
We’ll briefly go through each step and then show you the graph. Instead of going through steps 4 and 5 this time, we’ll try the alternative.
- 〰️ Find the domain of the function and determine if there are any discontinuities.
- Since this is a polynomial, the domain is all real numbers and there are no discontinuities.
- 🎯 Identify key features of the function, such as intercepts and symmetry.
- The x-intercept is and the y-intercept is .
- This function has neither even nor odd symmetry.
- 💯 Find critical points.
- By setting equal to 0 and factoring, we know that the function has critical points at and .
- 🥈 Alternative method: use the Second Derivative Test to determine the extrema of the function.
- . Since , this means the function is concave down at this point, and thus by the Second Derivative Test is a maximum.
- . Since , this means the function is concave up at this point, and thus by the Second Derivative Test is a minimum.
- ✏️ Determine points of inflection and intervals of concavity.
- is the only possible point of inflection. When we check concavity of the function to its left and right, we find that the function is concave down to the left of the point and concave up to the right of the point.
- Since the concavity of the function changes at , it is a point of inflection.
- 🎨 Putting it All Together!
- The y-intercept is .
- is a maximum.
- is a minimum.
- is a point of inflection (concave down to the left, concave up to the right)
We can plug these points into to get their exact y-values.
With this information, we see that looks like the following:
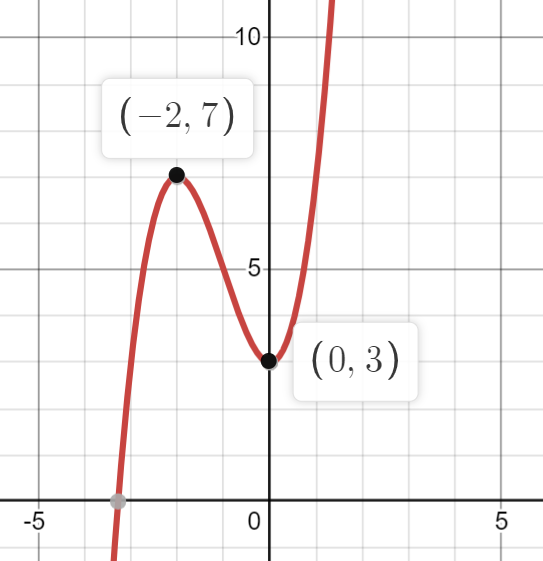
Image Created with Desmos.
⭐ Closing
You can follow these same steps for drawing the graph of the derivative of a function, and the second derivative. While you may not have to draw a graph from scratch on the AP exam, you will likely have to know how to determine the key information about a function from its graph, and drawing the graph can give you an in-depth understanding of these key features. ✍️
<< Hide Menu
5.8 Sketching Graphs of Functions and Their Derivatives
5 min read•june 18, 2024
Kashvi Panjolia
Kashvi Panjolia
5.8 My Combo
Previously you learned all about utilizing a function’s derivatives to find its increasing and decreasing intervals, relative and global extrema, concave up and concave down intervals, and more! Can we combine all this to form a complete image of a function’s graph? Yes, we can! Today, you’ll learn how to utilize all these tools in your toolbox to form an overall picture of a function.
📈 Sketching Graphs
Drawing the graphs of functions and their derivatives is very useful in determining key features of the function. From a graph, you can identify discontinuities, find critical points, and extrema, and discern many other important elements of a function.
There are seven steps to sketching a graph. This may seem like a lot, but once you break it down, you’ll get a hang of it! 🔎
- 〰️ Find the domain of the function and determine if there are any discontinuities.
- 🎯 Identify key features of the function, such as intercepts and symmetry.
- 💯 Find critical points.
- 📶 Determine where the function increases and decreases.
- 🤔 Find the extrema of the function.
- 🥈 An alternative to steps 4) and 5) is to use the Second Derivative Test to determine the extrema of the function.
- ✏️ Determine points of inflection and intervals of concavity.
And there we have it! An overview of what the entire function looks like! You can now use all these interesting points to sketch a graph of the function. 😄
🎨 Sketching Graphs Walkthrough
Now, let’s delve deeper into what each of these steps entails and sketch the following function!
〰️ Step 1) Find the domain and look for discontinuities.
A useful fact to memorize is that all polynomial functions have a domain consisting of all real numbers. Since we’re graphing a polynomial here, we know that the domain consists of all real numbers.
When looking for discontinuities, note if the function is rational or has any points where is not defined. Since there seem to be no points where is not defined, we can conclude that this function is continuous everywhere in its domain.
🎯 Step 2) Identify key features of the function, such as intercepts and symmetry.
First, let’s look for x-intercepts, where .
We can quickly do this by setting each factor equal to zero and solving for x.
And now, to set equal to 0.
This gives us two x-intercepts: and . The coordinates of these x-intercepts are and . Great! We got our first points we can plot.
Let’s now look for y-intercepts, where .
We have another point we can jot down to plot later! The coordinates of the y-intercept are .
Lastly, let’s look for symmetry. A function is symmetric with respect to a line if, when reflected across that line, the function looks the same as the original function. There are two types of symmetry a function may have:
- Even - the function is symmetrical across the y-axis. for all in the domain of the function.
- Odd - the function is symmetric about the origin. for all in the domain of the function.
If neither of these statements is true, the function has no symmetry. With our function, this is the case, so our function has no symmetry.

Image Courtesy of The Organic Chemistry Tutor
💯 Step 3) Find critical points.
If you recall from earlier sections of the unit, the first step of using a function’s derivative to determine its behavior involved finding critical points! These points occur when the function’s first derivative is equal to zero or is undefined.
The first derivative of our function is the following, using the product rule.
Setting this equal to zero and solving for x, we get and as the function’s critical points. We can use this information in the next step!
📶 Step 4) Determine where the function increases and decreases.
Using these critical points, we can determine the intervals where the function increases and decreases.
- ➕=📈 If the derivative of the function on the interval between two adjacent/nearest critical points is negative, then the function is decreasing on that interval.
- ➖=📉 If the derivative of the function is positive, then the function is increasing on that interval.
Please revisit our AP Calculus - 5.3 Determining Intervals on Which a Function Is Increasing or Decreasing guide for a more in-depth explanation!
Let’s evaluate the first derivative around each of our critical points:
| Interval | Verdict | ||
| is increasing | |||
| is decreasing | |||
| is increasing |
Whew! Now we know that is increasing between and and decreasing between .
🤔 Step 5) Find the extrema of the function.
Based on the information we discovered in the last step, we can easily apply the First Derivative Test to find the extrema of the function!
- ⬇️ The critical points where the function is decreasing on its left and increasing on its right are minimums.
- ⬆️ The critical points where the function is increasing on its left and decreasing on its right are maximums.
Visit our AP Calculus - 5.4 Using the First Derivative Test to Determine Relative (Local) Extrema guide if you need a refresher!
We know that to the left of , the function is increasing, and to the right of , the function is decreasing. Therefore, is a local maximum.
Vice versa is true for our critical point at . Since the function is decreasing to its left and increasing to its right, is a local minimum.
🥈 Alternative to Steps 4 & 5
An alternative to steps 4) and 5) is to use the Second Derivative Test to determine the extrema of the function. Recall that this test states that…
- If the second derivative of a function at a critical point is negative, then the function has a relative maximum at that point (and it’s concave down).
- If the second derivative of a function at a critical point is positive, then the function has a relative minimum at that point (and it’s concave up).
Please see our AP Calculus - 5.7 Using the Second Derivative Test to Determine Extrema guide.
✏️ Step 6) Determine points of inflection and concavity.
A function has a possible point of inflection if its second derivative is equal to zero at the point. To verify it is indeed a point of inflection, we must check to see if the function changes from concave up to concave down or vice versa (aka the second derivative changes from negative to positive or vice versa) on the two sides of the point.
For more information, revisit our AP Calculus - 5.6 Determining Concavity of Functions over Their Domains guide!
Here’s the second derivative of our function, .
Let’s find the possible point of inflection by setting this equal to 0.
Great! Now, we have to analyze the sign of the second derivative to see if this is a true point of inflection.
| Concavity | ||
| Concave down | ||
| Concave up |
Since the second derivative’s sign switches and the function’s concavity changes, is a point of inflection.
🎨 Putting it All Together!
Compiling all of the information we found, we know that:
- The function is continuous.
- We can plot , , and .
- is increasing between and .
- is decreasing between .
- is a local maximum.
- is a local minimum.
- Concavity changes at from concave down, to concave up.
And here we have it!

Image Created with Desmos.
You may not have needed all of the information we obtained, but having it all helps you double-check that you graphed correctly. Great work! 👏
📝 Sketching Graphs Practice
Try to sketch the following function on your own! What does the graph of look like?
Be sure to go through each step on your own before you scroll down further and see the answer!
✅ Sketching Graphs Question Solution
We’ll briefly go through each step and then show you the graph. Instead of going through steps 4 and 5 this time, we’ll try the alternative.
- 〰️ Find the domain of the function and determine if there are any discontinuities.
- Since this is a polynomial, the domain is all real numbers and there are no discontinuities.
- 🎯 Identify key features of the function, such as intercepts and symmetry.
- The x-intercept is and the y-intercept is .
- This function has neither even nor odd symmetry.
- 💯 Find critical points.
- By setting equal to 0 and factoring, we know that the function has critical points at and .
- 🥈 Alternative method: use the Second Derivative Test to determine the extrema of the function.
- . Since , this means the function is concave down at this point, and thus by the Second Derivative Test is a maximum.
- . Since , this means the function is concave up at this point, and thus by the Second Derivative Test is a minimum.
- ✏️ Determine points of inflection and intervals of concavity.
- is the only possible point of inflection. When we check concavity of the function to its left and right, we find that the function is concave down to the left of the point and concave up to the right of the point.
- Since the concavity of the function changes at , it is a point of inflection.
- 🎨 Putting it All Together!
- The y-intercept is .
- is a maximum.
- is a minimum.
- is a point of inflection (concave down to the left, concave up to the right)
We can plug these points into to get their exact y-values.
With this information, we see that looks like the following:

Image Created with Desmos.
⭐ Closing
You can follow these same steps for drawing the graph of the derivative of a function, and the second derivative. While you may not have to draw a graph from scratch on the AP exam, you will likely have to know how to determine the key information about a function from its graph, and drawing the graph can give you an in-depth understanding of these key features. ✍️

© 2024 Fiveable Inc. All rights reserved.