Browse By Unit
4.5 Solving Related Rates Problems
Welcome back to AP Calculus with Fiveable! In this session, we're diving into the world of related rates. Get ready to apply your calculus skills to real-world scenarios and solve problems that involve the rates at which quantities change with respect to time. 🕰️
🔗 Related Rates Basics
Related rates problems involve finding the rate at which a variable changes concerning the rate of change of another related variable. These scenarios may involve geometric figures and equations that connect different variables to time.
To review related rates, check out the previous Fiveable guide: Introduction to Related Rates.
🪜 Steps to Solve Related Rates Problems
When you first look at a related rates problem, you will be presented with so much information that you may feel overwhelmed. It’s okay to take a step back and organize before solving anything out!
The following steps will help you manage a related rates problem efficiently.
- 📚 Read the Problem Carefully: Identify values that are significant to the problem. You may find it helpful to circle, underline, or rewrite these values off to the side.
- ✏️ Draw a Diagram: Visualizing the situation by drawing a diagram can help us understand how each of the variables are changing. Make sure to accurately label variables and indicate their rates of change.
- 🏁 Set up an Equation: Use the information given to set up an equation that relates the variables involved. Usually, these equations are geometric, or given.
- 💫 Implicit Differentiation: Differentiate the equation implicitly with respect to time (t). This usually involves applying the chain rule to each term containing a variable.
- 🔌 Substitute Known Values: Substitute any known values and rates of change into the derivative equation.
- ✅ Solve for the Desired Rate: Solve the final equation for the rate you're asked to find. Be sure to check that your units match what is expected!
Time to put these steps to action…
🧮 Related Rates Practice Problems
Let’s work on a few questions and make sure we have the concept down!
1) Expanding Rectangle
An expanding rectangle has one side of length 6 feet and the other side of length 8 feet. If the length of the shorter side is increasing at a rate of 2 feet per minute, at what rate is the area of the rectangle increasing?
Let’s begin by identifying some key facts and drawing a picture of the scenario.
Known Information
- ft
- ft
Important Equations
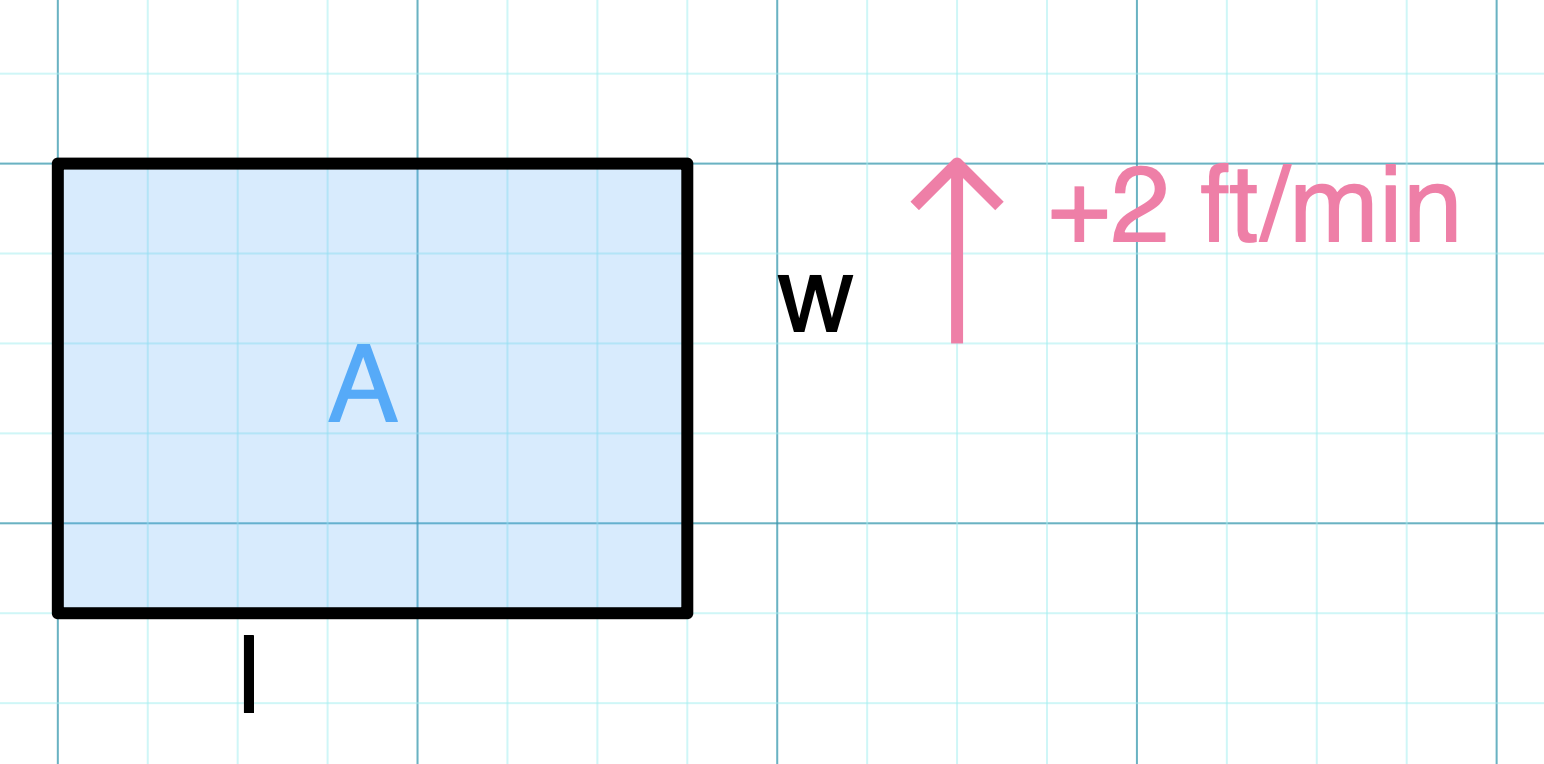
Image created with Virtual Graph Paper
Now we can set up the equation. When looking at the image, we notice that only one of the variables, the width, is changing. Since the length is not changing, we conclude that .
After directly plugging in any constants into the equation, we can find that the at any time. Now, let’s differentiate using the chain rule.
Therefore, the area of the rectangle is increasing at a rate of 16 feet per minute. Nice! 👍
2) Sliding Ladder
Consider a meter long ladder leaning against the wall. If the distance between the wall and the bottom of the ladder is increasing at m/s, how fast is the distance between the ground and the top of the ladder changing when the bottom of the ladder is feet away from the wall when it begins sliding?
This question unloaded a lot of information all at once, so take a second to reread the scenario before we get to work. You can do it! 🙌
Let’s begin by identifying some key facts and drawing a picture of the scenario.
Known Information
- m
Important Equations
-
- Pythagorean Theorem
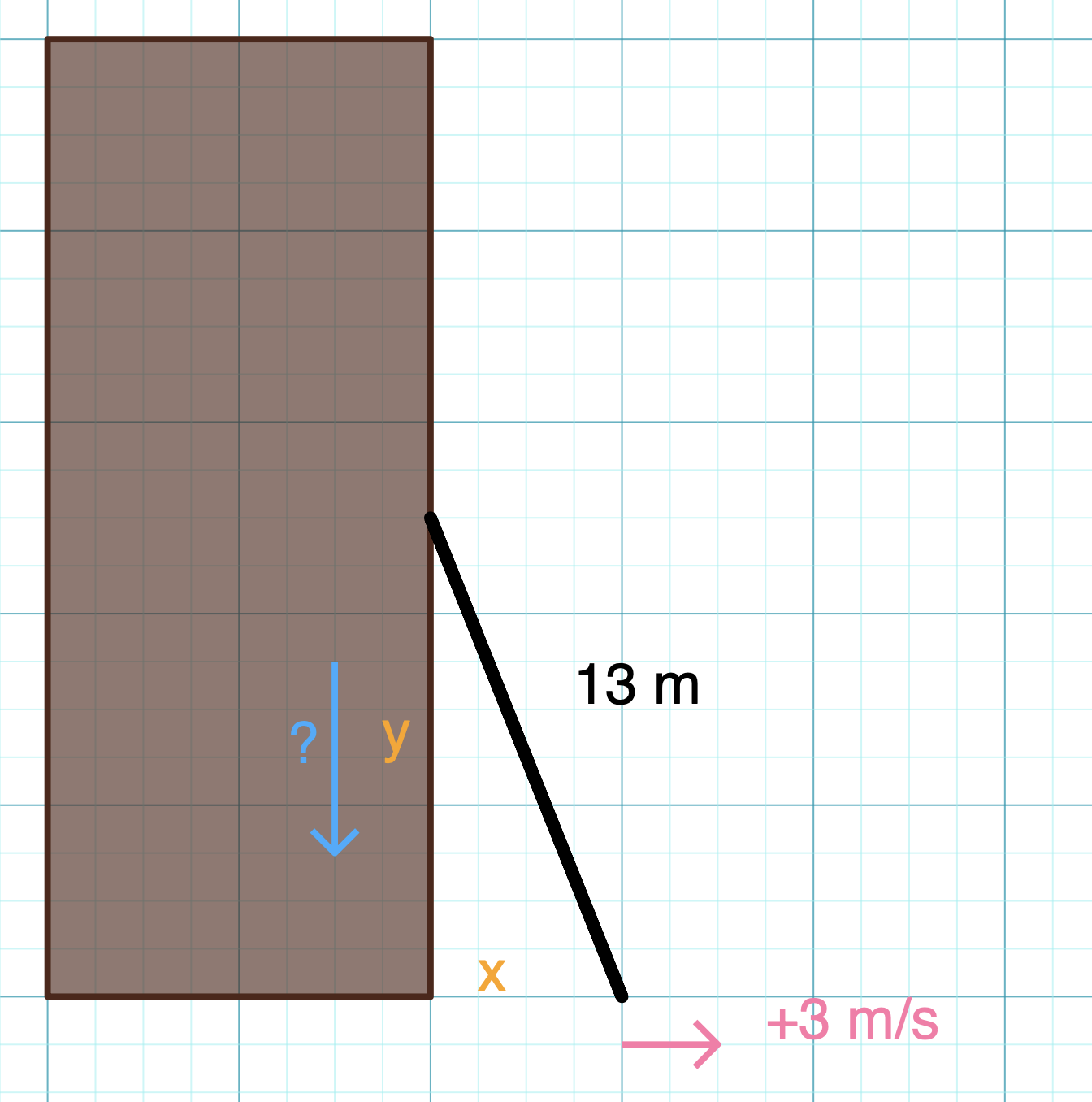
Image created with Virtual Graph Paper
Now we can use the equation relating the side lengths of the triangle made with the ladder, wall, and ground. When looking at the image, we notice that the hypotenuse of the triangle is not changing and we conclude that .
After directly plugging in any constants into the equation, we can relate the sides with the following equation: . And now we can finally take the derivative! Don’t forget to use the chain rule since we are taking the derivative with respect to time. Taking the derivative of the main equation gives us:
Now let’s plug in all known variables and see what we have to solve for.
You may have noticed that we have two missing pieces of information: the value of when and which is our ultimate solution.
We can solve for the value of by using the Pythagorean Theorem! A triangle will a side length of and a hypotenuse of is actually part of thre Pythagorean Triple . But if you didn’t pick that up, we can quickly solve for the missing value of by just plugging into the equation.
We can then isolate to get…
We're almost there!
The final step is to solve for . Using algebra, we can isolate and get and .
Therefore, we find that the distance between the top of the ladder and the ground is decreasing at a rate of meters per second when the bottom of the ladder is five feet away from the wall.
You’re on fire! Amazing job working through this difficult question. 🔥
🌟 Closing
Great work! 🙌 You now have the tools to tackle related rates problems. These types of questions often appear in the AP Calculus exam as both multiple choice and free response, challenging you to apply calculus concepts to real-world situations. Keep practicing, and you'll be able to solve related rates problems with ease!

Image Courtesy of Giphy
<< Hide Menu
4.5 Solving Related Rates Problems
Welcome back to AP Calculus with Fiveable! In this session, we're diving into the world of related rates. Get ready to apply your calculus skills to real-world scenarios and solve problems that involve the rates at which quantities change with respect to time. 🕰️
🔗 Related Rates Basics
Related rates problems involve finding the rate at which a variable changes concerning the rate of change of another related variable. These scenarios may involve geometric figures and equations that connect different variables to time.
To review related rates, check out the previous Fiveable guide: Introduction to Related Rates.
🪜 Steps to Solve Related Rates Problems
When you first look at a related rates problem, you will be presented with so much information that you may feel overwhelmed. It’s okay to take a step back and organize before solving anything out!
The following steps will help you manage a related rates problem efficiently.
- 📚 Read the Problem Carefully: Identify values that are significant to the problem. You may find it helpful to circle, underline, or rewrite these values off to the side.
- ✏️ Draw a Diagram: Visualizing the situation by drawing a diagram can help us understand how each of the variables are changing. Make sure to accurately label variables and indicate their rates of change.
- 🏁 Set up an Equation: Use the information given to set up an equation that relates the variables involved. Usually, these equations are geometric, or given.
- 💫 Implicit Differentiation: Differentiate the equation implicitly with respect to time (t). This usually involves applying the chain rule to each term containing a variable.
- 🔌 Substitute Known Values: Substitute any known values and rates of change into the derivative equation.
- ✅ Solve for the Desired Rate: Solve the final equation for the rate you're asked to find. Be sure to check that your units match what is expected!
Time to put these steps to action…
🧮 Related Rates Practice Problems
Let’s work on a few questions and make sure we have the concept down!
1) Expanding Rectangle
An expanding rectangle has one side of length 6 feet and the other side of length 8 feet. If the length of the shorter side is increasing at a rate of 2 feet per minute, at what rate is the area of the rectangle increasing?
Let’s begin by identifying some key facts and drawing a picture of the scenario.
Known Information
- ft
- ft
Important Equations

Image created with Virtual Graph Paper
Now we can set up the equation. When looking at the image, we notice that only one of the variables, the width, is changing. Since the length is not changing, we conclude that .
After directly plugging in any constants into the equation, we can find that the at any time. Now, let’s differentiate using the chain rule.
Therefore, the area of the rectangle is increasing at a rate of 16 feet per minute. Nice! 👍
2) Sliding Ladder
Consider a meter long ladder leaning against the wall. If the distance between the wall and the bottom of the ladder is increasing at m/s, how fast is the distance between the ground and the top of the ladder changing when the bottom of the ladder is feet away from the wall when it begins sliding?
This question unloaded a lot of information all at once, so take a second to reread the scenario before we get to work. You can do it! 🙌
Let’s begin by identifying some key facts and drawing a picture of the scenario.
Known Information
- m
Important Equations
-
- Pythagorean Theorem

Image created with Virtual Graph Paper
Now we can use the equation relating the side lengths of the triangle made with the ladder, wall, and ground. When looking at the image, we notice that the hypotenuse of the triangle is not changing and we conclude that .
After directly plugging in any constants into the equation, we can relate the sides with the following equation: . And now we can finally take the derivative! Don’t forget to use the chain rule since we are taking the derivative with respect to time. Taking the derivative of the main equation gives us:
Now let’s plug in all known variables and see what we have to solve for.
You may have noticed that we have two missing pieces of information: the value of when and which is our ultimate solution.
We can solve for the value of by using the Pythagorean Theorem! A triangle will a side length of and a hypotenuse of is actually part of thre Pythagorean Triple . But if you didn’t pick that up, we can quickly solve for the missing value of by just plugging into the equation.
We can then isolate to get…
We're almost there!
The final step is to solve for . Using algebra, we can isolate and get and .
Therefore, we find that the distance between the top of the ladder and the ground is decreasing at a rate of meters per second when the bottom of the ladder is five feet away from the wall.
You’re on fire! Amazing job working through this difficult question. 🔥
🌟 Closing
Great work! 🙌 You now have the tools to tackle related rates problems. These types of questions often appear in the AP Calculus exam as both multiple choice and free response, challenging you to apply calculus concepts to real-world situations. Keep practicing, and you'll be able to solve related rates problems with ease!

Image Courtesy of Giphy

© 2024 Fiveable Inc. All rights reserved.