Browse By Unit
Sumi Vora
Sumi Vora
In this unit, you will learn more about derivatives, how they are defined, and the basic derivative rules (and exceptions). As one of the core foundations of analyzing functions and change in calculus itself, it is of utmost importance to gain an in-depth understanding of this unit before moving forward to more advanced concepts.📑 This unit makes up 10-12% of the Calculus AB exam and 4-7% of the Calculus BC exam.
This list will be a good place to start in terms of self-assessing what you need to study or learn. 📖 It will also (hopefully) help you intuit a lot of the concepts that you will learn later in calculus. You can get into the nitty gritty later, but for now, try to focus on really understanding. As you are looking through this list, write down what topics you don’t remember or still need to learn. You can then go to the full study guide page for each topic to get some more information!
What is a derivative?
Suppose we are watching Michael Phelps swim a 200m race, and on this particular day, he takes 1 minute and 40 seconds to complete it. If I asked you his average speed, you might use the formula speed = distance/time and say that his average speed was 200m/100s = 2 m/s. But, he didn't swim the whole race at exactly the same speed. Maybe I want to know which exact time in the race he was swimming the fastest, or maybe I want to know his speed at exactly the 1 minute mark. "But you can't find speed for just one instant in time! That doesn't make any sense!" you might argue. You would be correct. However, we have a little work-around to approximate this speed.
First, I want to define a real-valued function with time (t) on the horizontal axis and position (s) on the vertical axis. You could switch around the axes, but you'll see why making this particular choice makes sense in just a second. Now, the speed for some interval will just be the slope of the function in some particular interval, since slope = change in vertical axis / change in horizontal axis = change in distance / change in speed. Now, we need to figure out how to approximate the slope for one particular value of t. We can take a really small interval, say 0.1 seconds, and say that the speed can't change much within such a small time frame, so this is a pretty good approximation. Then, the slope would be given by:
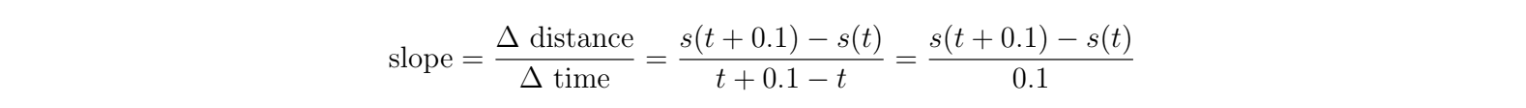
But maybe an interval of 0.1 seconds isn't good enough for us. Maybe we want 0.01, or 0.00001 seconds. As the interval decreases towards 0, the closer we get to estimating the actual instantaneous speed. Let's use the variable dt to denote the size of the interval. Then, the instantaneous rate of speed is given by:
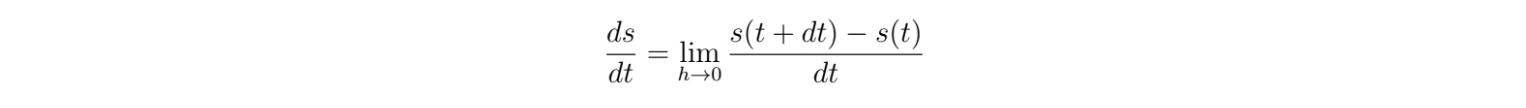
The instantaneous rate of change of a function is called the derivative. Usually, we say "the derivative with respect to _". In this case, it will be "the derivative with respect to t," since we are finding the rate of change of position with respect to time.
Notice that the deltas changed to ds in this equation. In math, whenever you see d's, we usually thing derivatives or differential equations.
I did this example using ds/dt, because this is what we usually use when we're talking about velocity and speeds. But, you'll often find derivatives defined in the xy-plane, and instead of using small dx's, we'll use h to denote the small change in x. For some real-valued function f on the xy-plane, the derivative of f with respect to x is:

You will also see the notation f'(x) or y' (read f prime of x or y prime) for derivatives in two-dimensional spaces. This is okay and you should be familiar with the notation, but it is good to get into the habit of writing it in the form dy/dx because this notation is used more in the real world (where there are more than two variables).
The derivative is the slope of the tangent line!
Given that the derivative is the instantaneous slope of a function, the derivative is also the slope of the tangent line of the function at that point. Make sure to remember this! There will be lots of applications later on.
A good way to intuit this idea is to imagine zooming in on the function, so you can approximate the slope of the function at some point as just a line. This is the tangent line. This line will just touch the function, For simplicity's sake, some books will say that the tangent line only touches the function at one point. However, this isn't always true, so don't stress if your tangent line crosses the function at another point.
An important part of the definition of a derivative is that for some point, there will only exist one derivative. That implies that there will only exist one tangent line. There are some functions, like piecewise functions and absolute value functions, where you could hypothetically draw two or three or an infinite number of tangent lines to the function. If that is the case, it is a good indication that the derivative doesn't exist. Additionally, if you draw a tangent line and the line is exactly vertical, that means that the slope is infinity, which means that the derivative is undefined. In general, a good heuristic is that if the function is smooth, continuous, and has a non-vertical slope, then the derivative exists.
Here's an example of a function with a vertical tangent line:

Computing Derivatives
Here are some good-to-know properties of derivatives. There are some good intuitive geometric explanations for why the sum, product, and quotient rules make sense, but it is usually easier to just use the formulas. However, don't spend too much time memorizing these. You can just do a few practice problems and get the hang of it.
- Constant Rule: the derivative of any constant is 0
- Constant Multiple Rule: if you have a function with a constant multiplied by an expression, the derivative of the function is just the derivative of the expression times the constant. For example, d/dx(3x) = 3 * d/dx(x)
- Sum Rule: if you have two expressions that are added together in a function, then the derivative of the function is the sum of the derivatives of these expressions. For example, if you have f(x) = sin(x) + 3x, then f'(x) = d/dx(sin(x)) + d/dx(3x)
- Product Rule: The product rule helps you find the derivative of two expressions multiplied together. If h(x) = f(x) g(x), then h'(x) = f'(x)g(x) + f(x)g'(x)
- Quotient Rule: The quotient rule comes from the product rule. If you want to find the derivative of h(x) = f(x)/g(x) = f(x) g⁻¹(x), then h'(x) = (f'(x)g(x) - f(x)g'(x))/(g(x))² There are several formulas available for computing derivatives. This can make finding derivatives very easy, but it somewhat obfuscates the definition and applications of derivatives. However, it is important to remember that these formulas are just derived from the definition of the derivative. Here is a simple example:
Suppose you want to find the derivative of the function f(x) = xⁿ*.* Then, we get:
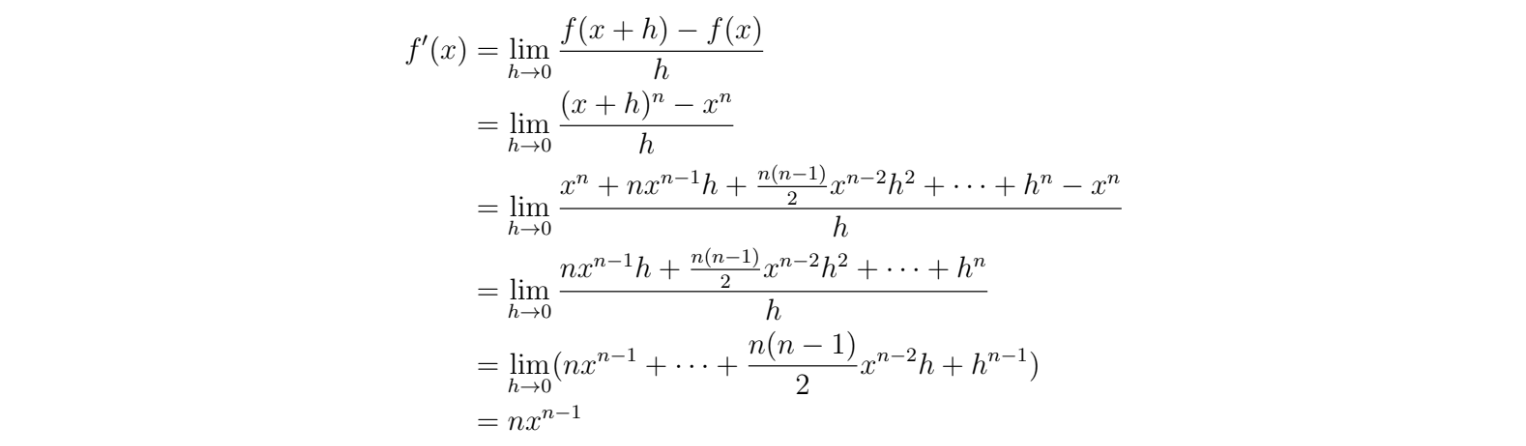
This is called the power rule.
Special Derivatives
There are some special functions that we should just know the derivatives for. Here they are:
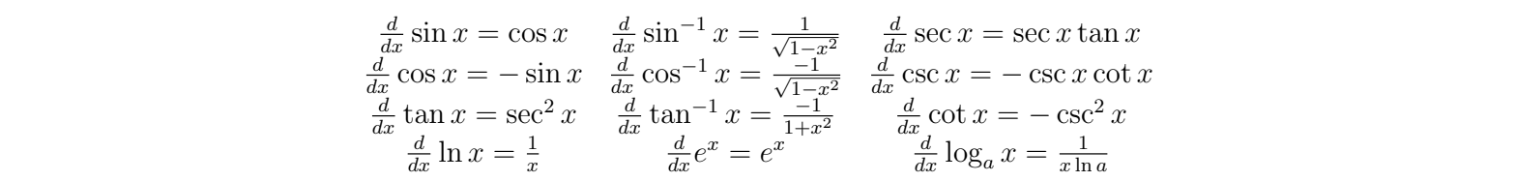
Example:
Find the derivative of f(x) = x³ + 3x ln(x) + 5
Solution:

<< Hide Menu
Sumi Vora
Sumi Vora
In this unit, you will learn more about derivatives, how they are defined, and the basic derivative rules (and exceptions). As one of the core foundations of analyzing functions and change in calculus itself, it is of utmost importance to gain an in-depth understanding of this unit before moving forward to more advanced concepts.📑 This unit makes up 10-12% of the Calculus AB exam and 4-7% of the Calculus BC exam.
This list will be a good place to start in terms of self-assessing what you need to study or learn. 📖 It will also (hopefully) help you intuit a lot of the concepts that you will learn later in calculus. You can get into the nitty gritty later, but for now, try to focus on really understanding. As you are looking through this list, write down what topics you don’t remember or still need to learn. You can then go to the full study guide page for each topic to get some more information!
What is a derivative?
Suppose we are watching Michael Phelps swim a 200m race, and on this particular day, he takes 1 minute and 40 seconds to complete it. If I asked you his average speed, you might use the formula speed = distance/time and say that his average speed was 200m/100s = 2 m/s. But, he didn't swim the whole race at exactly the same speed. Maybe I want to know which exact time in the race he was swimming the fastest, or maybe I want to know his speed at exactly the 1 minute mark. "But you can't find speed for just one instant in time! That doesn't make any sense!" you might argue. You would be correct. However, we have a little work-around to approximate this speed.
First, I want to define a real-valued function with time (t) on the horizontal axis and position (s) on the vertical axis. You could switch around the axes, but you'll see why making this particular choice makes sense in just a second. Now, the speed for some interval will just be the slope of the function in some particular interval, since slope = change in vertical axis / change in horizontal axis = change in distance / change in speed. Now, we need to figure out how to approximate the slope for one particular value of t. We can take a really small interval, say 0.1 seconds, and say that the speed can't change much within such a small time frame, so this is a pretty good approximation. Then, the slope would be given by:
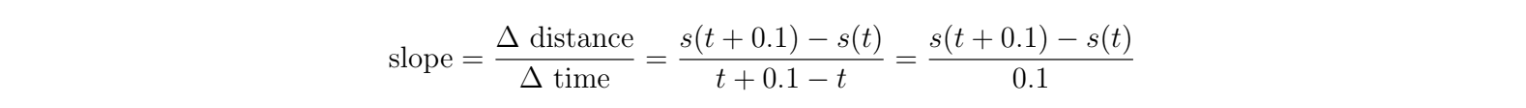
But maybe an interval of 0.1 seconds isn't good enough for us. Maybe we want 0.01, or 0.00001 seconds. As the interval decreases towards 0, the closer we get to estimating the actual instantaneous speed. Let's use the variable dt to denote the size of the interval. Then, the instantaneous rate of speed is given by:
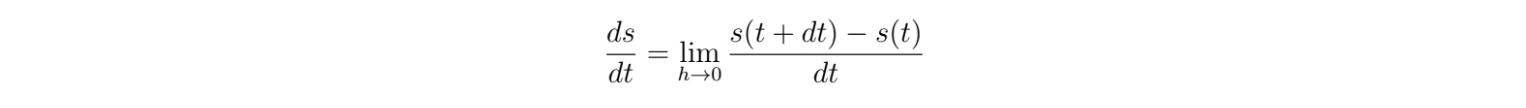
The instantaneous rate of change of a function is called the derivative. Usually, we say "the derivative with respect to _". In this case, it will be "the derivative with respect to t," since we are finding the rate of change of position with respect to time.
Notice that the deltas changed to ds in this equation. In math, whenever you see d's, we usually thing derivatives or differential equations.
I did this example using ds/dt, because this is what we usually use when we're talking about velocity and speeds. But, you'll often find derivatives defined in the xy-plane, and instead of using small dx's, we'll use h to denote the small change in x. For some real-valued function f on the xy-plane, the derivative of f with respect to x is:

You will also see the notation f'(x) or y' (read f prime of x or y prime) for derivatives in two-dimensional spaces. This is okay and you should be familiar with the notation, but it is good to get into the habit of writing it in the form dy/dx because this notation is used more in the real world (where there are more than two variables).
The derivative is the slope of the tangent line!
Given that the derivative is the instantaneous slope of a function, the derivative is also the slope of the tangent line of the function at that point. Make sure to remember this! There will be lots of applications later on.
A good way to intuit this idea is to imagine zooming in on the function, so you can approximate the slope of the function at some point as just a line. This is the tangent line. This line will just touch the function, For simplicity's sake, some books will say that the tangent line only touches the function at one point. However, this isn't always true, so don't stress if your tangent line crosses the function at another point.
An important part of the definition of a derivative is that for some point, there will only exist one derivative. That implies that there will only exist one tangent line. There are some functions, like piecewise functions and absolute value functions, where you could hypothetically draw two or three or an infinite number of tangent lines to the function. If that is the case, it is a good indication that the derivative doesn't exist. Additionally, if you draw a tangent line and the line is exactly vertical, that means that the slope is infinity, which means that the derivative is undefined. In general, a good heuristic is that if the function is smooth, continuous, and has a non-vertical slope, then the derivative exists.
Here's an example of a function with a vertical tangent line:

Computing Derivatives
Here are some good-to-know properties of derivatives. There are some good intuitive geometric explanations for why the sum, product, and quotient rules make sense, but it is usually easier to just use the formulas. However, don't spend too much time memorizing these. You can just do a few practice problems and get the hang of it.
- Constant Rule: the derivative of any constant is 0
- Constant Multiple Rule: if you have a function with a constant multiplied by an expression, the derivative of the function is just the derivative of the expression times the constant. For example, d/dx(3x) = 3 * d/dx(x)
- Sum Rule: if you have two expressions that are added together in a function, then the derivative of the function is the sum of the derivatives of these expressions. For example, if you have f(x) = sin(x) + 3x, then f'(x) = d/dx(sin(x)) + d/dx(3x)
- Product Rule: The product rule helps you find the derivative of two expressions multiplied together. If h(x) = f(x) g(x), then h'(x) = f'(x)g(x) + f(x)g'(x)
- Quotient Rule: The quotient rule comes from the product rule. If you want to find the derivative of h(x) = f(x)/g(x) = f(x) g⁻¹(x), then h'(x) = (f'(x)g(x) - f(x)g'(x))/(g(x))² There are several formulas available for computing derivatives. This can make finding derivatives very easy, but it somewhat obfuscates the definition and applications of derivatives. However, it is important to remember that these formulas are just derived from the definition of the derivative. Here is a simple example:
Suppose you want to find the derivative of the function f(x) = xⁿ*.* Then, we get:
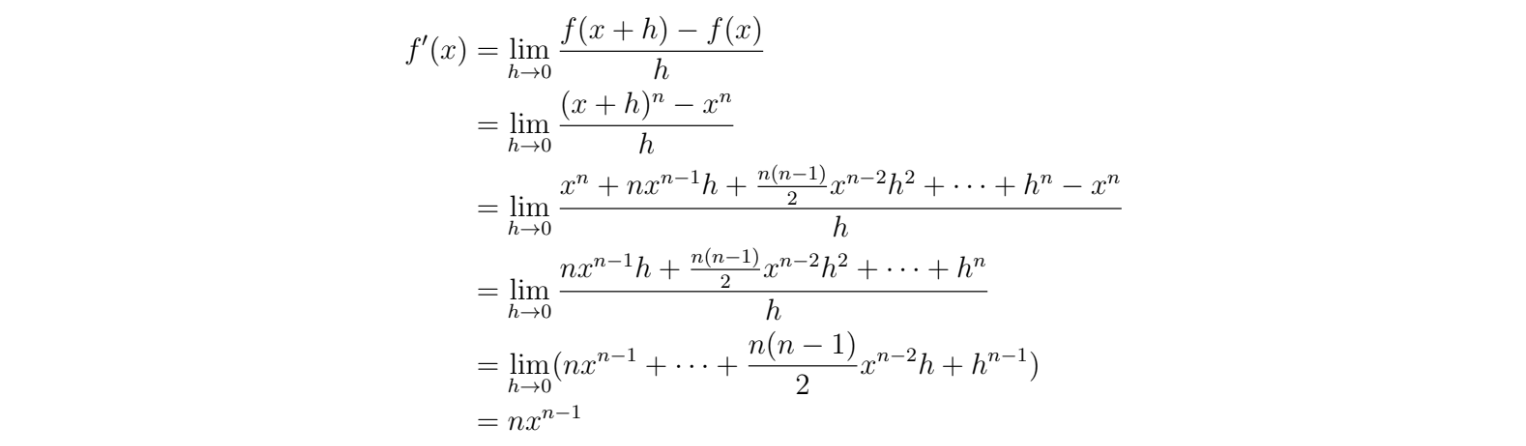
This is called the power rule.
Special Derivatives
There are some special functions that we should just know the derivatives for. Here they are:
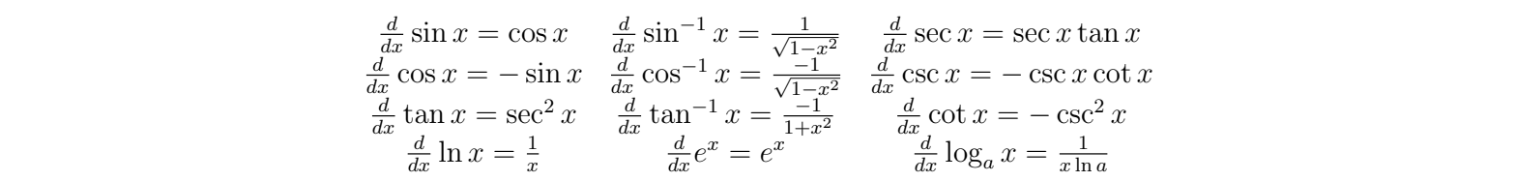
Example:
Find the derivative of f(x) = x³ + 3x ln(x) + 5
Solution:


© 2024 Fiveable Inc. All rights reserved.