Browse By Unit
10.4 Integral Test for Convergence
Welcome to AP Calc 10.4! In this guide, you’ll learn how to apply another test to determine whether series are convergent or divergent. This test will rely heavily on your understanding of indefinite integrals from Unit 6.
∫ Integral Test Theorem
The integral test states that, for a positive, decreasing function over the interval with a corresponding sequence , then…
(1) if converges, then also converges,
(2) if diverges, then also diverges,
and…
For now, we can ignore the comparison portion and just focus on the first points! Let’s break down what everything means.
🧱 Breaking Down the Integral Test Theorem
First, we need a positive, decreasing function. This means it must be above zero over the entire interval, and decreasing, or getting smaller over time. Consider the function over the interval :
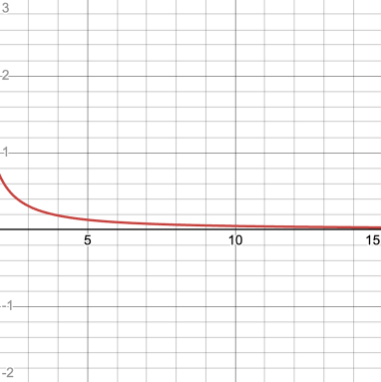
Image courtesy of Desmos
This function satisfies our initial condition. Now, we just need a series where . This is pretty easy to set up!
Now, we can apply our test!
✏️ Applying the Integral Theorem
To apply our test, we first have to take the integral of our function:
To solve this integral, we need to apply -substitution, where and :
Undoing -substitution, we find that
Finally, we evaluate over our bounds:
Because this integral evaluates as , we say it is divergent. Based on our theorem, this means that the series is also divergent.
📝 Integral Test Theorem Practice
Now it’s your turn to apply what you’ve learned!
❓Integral Test Theorem Problems
-
State the integral test and its conditions.
-
Use the integral test to determine whether the series diverges.
-
Use the integral test to determine whether the series diverges.
💡 Integral Test Theorem Solutions
-
Review the beginning of the guide for the full theorem! You need a function that is decreasing and positive over an interval and a series using that function.
-
The integral is a standard integral, giving which gives , which means that the series is convergent.
-
The integral is evaluated using -substitution, where and :
Undoing -substitution, we get:
Because the integral is not finite, we say it diverges. Therefore, our series diverges.
Excellent job! Be sure to practice this type of problem and make sure you know the conditions for using this test. Once you’ve got it down, the integral test will be a breeze! 💯
<< Hide Menu
10.4 Integral Test for Convergence
Welcome to AP Calc 10.4! In this guide, you’ll learn how to apply another test to determine whether series are convergent or divergent. This test will rely heavily on your understanding of indefinite integrals from Unit 6.
∫ Integral Test Theorem
The integral test states that, for a positive, decreasing function over the interval with a corresponding sequence , then…
(1) if converges, then also converges,
(2) if diverges, then also diverges,
and…
For now, we can ignore the comparison portion and just focus on the first points! Let’s break down what everything means.
🧱 Breaking Down the Integral Test Theorem
First, we need a positive, decreasing function. This means it must be above zero over the entire interval, and decreasing, or getting smaller over time. Consider the function over the interval :

Image courtesy of Desmos
This function satisfies our initial condition. Now, we just need a series where . This is pretty easy to set up!
Now, we can apply our test!
✏️ Applying the Integral Theorem
To apply our test, we first have to take the integral of our function:
To solve this integral, we need to apply -substitution, where and :
Undoing -substitution, we find that
Finally, we evaluate over our bounds:
Because this integral evaluates as , we say it is divergent. Based on our theorem, this means that the series is also divergent.
📝 Integral Test Theorem Practice
Now it’s your turn to apply what you’ve learned!
❓Integral Test Theorem Problems
-
State the integral test and its conditions.
-
Use the integral test to determine whether the series diverges.
-
Use the integral test to determine whether the series diverges.
💡 Integral Test Theorem Solutions
-
Review the beginning of the guide for the full theorem! You need a function that is decreasing and positive over an interval and a series using that function.
-
The integral is a standard integral, giving which gives , which means that the series is convergent.
-
The integral is evaluated using -substitution, where and :
Undoing -substitution, we get:
Because the integral is not finite, we say it diverges. Therefore, our series diverges.
Excellent job! Be sure to practice this type of problem and make sure you know the conditions for using this test. Once you’ve got it down, the integral test will be a breeze! 💯

© 2024 Fiveable Inc. All rights reserved.