Browse By Unit
1.2 Defining Limits and Using Limit Notation
1 min read•june 18, 2024
In this study guide, we’ll review how limits can be defined and how to use limit notation. Understanding limits is like peeking into the future of a function as it approaches a specific value. By the end of this reading, you’ll have a strong grasp of this critical AP Calculus skill. Let's get started by breaking down the key aspects of defining limits and using different notation forms.
🤔 Defining a Limit
At its core, a limit is the y-value of a function, , when it approaches the value . Commonly, it is notated as , which is read as “the limit of as approaches ”.
The visual below breaks down the different parts of the equation, which is how we represent limits analytically:
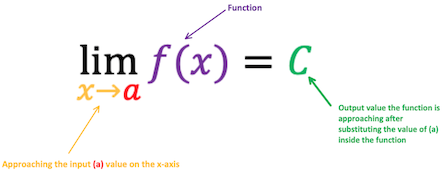
Image Courtesy of Study.com
This notation tells us that as x gets closer and closer to the value , the function f(x) inches closer and closer to the real number . Remember that the limit is not equal to , but rather gets closer and closer to it.
🤨 Representing Limits Numerically & Graphically
Limits can also be expressed numerically and graphically. Numerically, you might create a table of values approaching from both sides. Graphically, you can observe how the function approaches a certain height as gets closer to .
🔢 Representing Limits Numerically
Consider the following function:
We're interested in finding the limit of this function as approaches .
Let's set up a table of values where approaches from both the left and the right side:
| Approaching from the left () | Approaching from the left () |
| 0.9 | 1.1 |
| 0.99 | 1.01 |
| 0.999 | 1.001 |
| 0.9999 | 1.0001 |
Notice how we’re getting as closer as possible to the value 1 from both the right and left sides. Now, let’s calculate the corresponding values of by plugging each of these values in.
⬅️ Viewing the Limit from the Left Side
For :
When plugging in …
When plugging in …
When plugging in …
When plugging in …
We can already see that as gets closer and closer to , approaches and gets closer to .
➡️ Viewing the Limit from the Right Side
For :
When plugging in …
When plugging in …
When plugging in …
When plugging in …
We can also see that as gets closer to 1 from the right side, gets closer to 2! This suggests that:
This numerical representation really shows you how the function approaches a particular value as x gets arbitrarily close to the specified value.
We’ll get into estimating limit values from tables in key topic 1.4! This just gives you an idea of how limits can be represented numerically. 😄
📉 Representing Limits Graphically
Consider the linear function . We want to investigate the limit of this function as approaches 1, or . As approaches 1, let's visualize how the function behaves graphically.
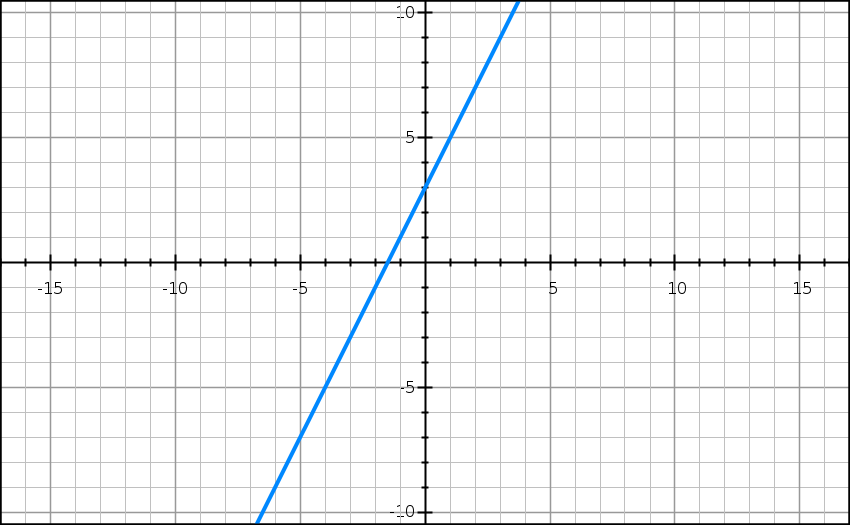
Image Courtesy of GraphSketch.com
As approaches 1 from the left and from the right , the function values smoothly progress along the straight line, converging towards a specific y-value. This limit statement indicates that as gets arbitrarily close to 1, the function approaches the value 5.
We’ll get into estimating limits from graphs more in the next key topic!
✏️Defining Limits: Practice Problems
When you go through these two practice problems, think of going through two different steps:
- ⚡ Substitute the value into the limit.
- 🧮 Evaluate the limit.
Go ahead and give it a try!
-
Consider the function . What is the value of ?
A. 3
B. 5
C. 6
D. 7
-
Consider the function . What is the value of ?
A. -8
B. 8
C. 9
D. 1
☑️ Defining Limits: Solutions to Practice Problems
-
To solve this question, follow these steps:
- Substitute the value: =
- Evaluate the limit: Substitute
Therefore, the correct answer is: B) 5
-
To solve this question, follow these steps:
- Substitute the value: =
- Evaluate the limit: Substitute
Therefore, the correct answer is: A) -8
<< Hide Menu
1.2 Defining Limits and Using Limit Notation
1 min read•june 18, 2024
In this study guide, we’ll review how limits can be defined and how to use limit notation. Understanding limits is like peeking into the future of a function as it approaches a specific value. By the end of this reading, you’ll have a strong grasp of this critical AP Calculus skill. Let's get started by breaking down the key aspects of defining limits and using different notation forms.
🤔 Defining a Limit
At its core, a limit is the y-value of a function, , when it approaches the value . Commonly, it is notated as , which is read as “the limit of as approaches ”.
The visual below breaks down the different parts of the equation, which is how we represent limits analytically:
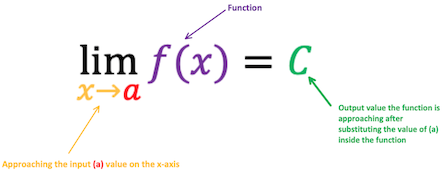
Image Courtesy of Study.com
This notation tells us that as x gets closer and closer to the value , the function f(x) inches closer and closer to the real number . Remember that the limit is not equal to , but rather gets closer and closer to it.
🤨 Representing Limits Numerically & Graphically
Limits can also be expressed numerically and graphically. Numerically, you might create a table of values approaching from both sides. Graphically, you can observe how the function approaches a certain height as gets closer to .
🔢 Representing Limits Numerically
Consider the following function:
We're interested in finding the limit of this function as approaches .
Let's set up a table of values where approaches from both the left and the right side:
| Approaching from the left () | Approaching from the left () |
| 0.9 | 1.1 |
| 0.99 | 1.01 |
| 0.999 | 1.001 |
| 0.9999 | 1.0001 |
Notice how we’re getting as closer as possible to the value 1 from both the right and left sides. Now, let’s calculate the corresponding values of by plugging each of these values in.
⬅️ Viewing the Limit from the Left Side
For :
When plugging in …
When plugging in …
When plugging in …
When plugging in …
We can already see that as gets closer and closer to , approaches and gets closer to .
➡️ Viewing the Limit from the Right Side
For :
When plugging in …
When plugging in …
When plugging in …
When plugging in …
We can also see that as gets closer to 1 from the right side, gets closer to 2! This suggests that:
This numerical representation really shows you how the function approaches a particular value as x gets arbitrarily close to the specified value.
We’ll get into estimating limit values from tables in key topic 1.4! This just gives you an idea of how limits can be represented numerically. 😄
📉 Representing Limits Graphically
Consider the linear function . We want to investigate the limit of this function as approaches 1, or . As approaches 1, let's visualize how the function behaves graphically.

Image Courtesy of GraphSketch.com
As approaches 1 from the left and from the right , the function values smoothly progress along the straight line, converging towards a specific y-value. This limit statement indicates that as gets arbitrarily close to 1, the function approaches the value 5.
We’ll get into estimating limits from graphs more in the next key topic!
✏️Defining Limits: Practice Problems
When you go through these two practice problems, think of going through two different steps:
- ⚡ Substitute the value into the limit.
- 🧮 Evaluate the limit.
Go ahead and give it a try!
-
Consider the function . What is the value of ?
A. 3
B. 5
C. 6
D. 7
-
Consider the function . What is the value of ?
A. -8
B. 8
C. 9
D. 1
☑️ Defining Limits: Solutions to Practice Problems
-
To solve this question, follow these steps:
- Substitute the value: =
- Evaluate the limit: Substitute
Therefore, the correct answer is: B) 5
-
To solve this question, follow these steps:
- Substitute the value: =
- Evaluate the limit: Substitute
Therefore, the correct answer is: A) -8

© 2024 Fiveable Inc. All rights reserved.