Browse By Unit
1.11 Defining Continuity at a Point
Now that we’ve explored different types of discontinuity, we can dive into what continuity really is and how we can define it at a point. 🎯
What is Continuity?
Continuity means that a function behaves smoothly and doesn't have sudden jumps or gaps in its graph. It's like drawing a line without lifting your pen. To check if a function is continuous, we make sure it's not broken or full of holes, and it behaves predictably as we get closer to specific points. This concept is important, especially in calculus and real analysis, to understand how functions change and interact.
On the AP exam, you’re going to have to be able to justify WHY something is continuous (or not continuous). Let's explore ways to figure out if a function is continuous!
Defining Continuity
A function f(x) is continuous at a specific point 'c' in its domain if the following three conditions are met:
1️⃣ f(c) is defined (i.e., there is a value of the function at c)
2️⃣ The limit of the function as x approaches c exists
3️⃣ The value of the function at c (f(c)) is equal to the limit of the function as x approaches c. In other words, .
Defining Continuity With A Graph
To prove that a line is continuous at a specific point using a graph, you'll need to ensure that there are no jumps, gaps, or breaks in the graph at that point. The key is to visually demonstrate that the line flows smoothly without any interruptions. Here's how you can do it:
- 📈 Plot the Graph: Start by plotting the graph of the line. Make sure it's accurate and well-drawn.
- 🤓 Focus on the Point of Interest: Identify the specific point at which you want to prove continuity.
- ⛳ Check for a Continuous Connection: Examine the graph very closely as you approach the point from both the left and the right sides. Make sure that the line doesn't have any sudden jumps or holes.
- If the line connects smoothly as you get closer to the point from both sides, it's a sign of continuity.
- If there's a noticeable gap, jump, or any kind of interruption in the graph at that point, it's not continuous.
- 🏷️ Use Labels and Annotations: To make your case clear, you can label the point in question and perhaps mark the paths approaching it from both sides. You might also annotate the graph with a note like "Continuous at this point" or "Discontinuous at this point" to highlight your conclusion.
- 🤯 Provide an Explanation: Alongside the graph, explain why the line is continuous at that point. For example, you can state that the value of the function at the point matches the limit from both directions. Alternatively, if it's discontinuous, explain the specific reason for the discontinuity.
Examples: Defining Continuity in Graphs
For example, take a look at these graphs:
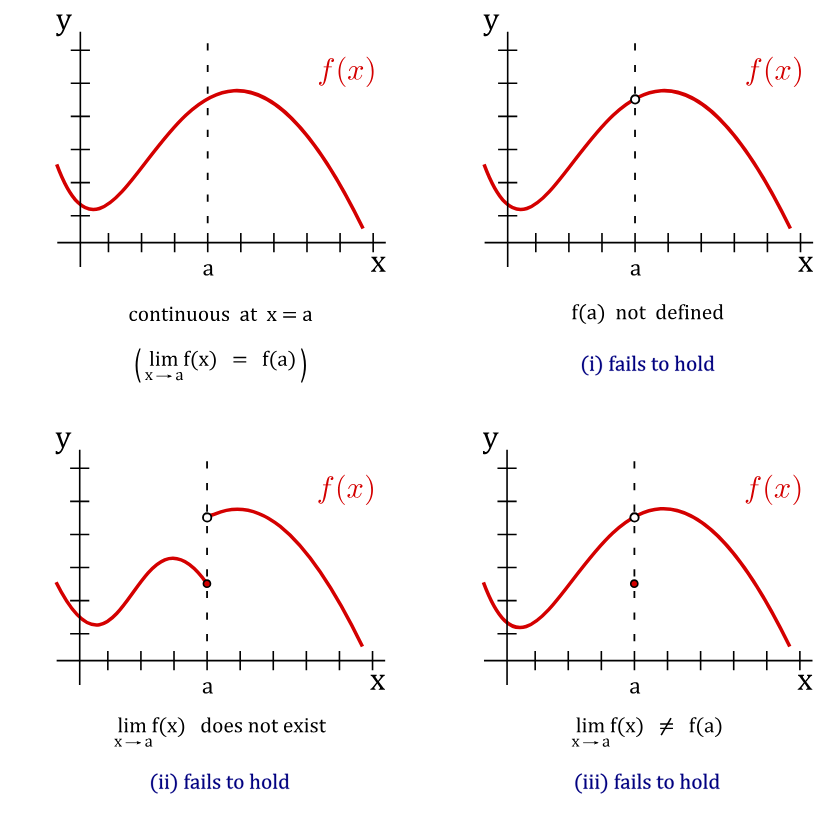
Image courtesy of SFU.ca
In this example, only the top left graph is continuous. On all other graphs, there is a skip which makes the graph discontinuous at that point. Below the graphs are explanations as to why the graph is not continuous. These explanations are what we should aim for!
Defining Continuity: Practice Questions
Defining Continuity: Question 1
Is the function continuous at ? Justify your conclusion using the definition.
Explanation: To check continuity, we need to ensure three things:
- f(2) exists (It's 3 * 2 + 5 = 11, so it's a real number).
- The limit as x approaches 2 exists.
- The limit matches the value (limit = 11).
Defining Continuity: Question 2
Consider the functions and . Are both functions continuous at ? Justify your conclusions using the definition.
Explanation: For each function, apply the definition of continuity:
- Check if f(3) and g(3) are defined ( and ).
- Calculate the limits as x approaches 3 for both functions.
- For f(x), the limit as x approaches 3 is also 9 (matching ).
- For g(x), the limit as x approaches 3 is 6 (matching ).
Perfect, both functions are continuous at x = 3. ✏️
Defining Continuity: Question 3
Examine the functions and . Are both functions continuous at ? Justify your answer.
Explanation:
- Check if p(0) and q(0) are defined (, which is undefined, and , a real number).
- Calculate the limits as x approaches 0 for both functions.
- For p(x), the limit as x approaches 0 is undefined (division by zero), which doesn't match p(0).
- For q(x), the limit as x approaches 0 is 0, which matches q(0).
Therefore, function q(x) is continuous at x = 0, while p(x) is not continuous at x = 0.
Problem-Solving Tips
Good luck, you got this! 🍀
<< Hide Menu
1.11 Defining Continuity at a Point
Now that we’ve explored different types of discontinuity, we can dive into what continuity really is and how we can define it at a point. 🎯
What is Continuity?
Continuity means that a function behaves smoothly and doesn't have sudden jumps or gaps in its graph. It's like drawing a line without lifting your pen. To check if a function is continuous, we make sure it's not broken or full of holes, and it behaves predictably as we get closer to specific points. This concept is important, especially in calculus and real analysis, to understand how functions change and interact.
On the AP exam, you’re going to have to be able to justify WHY something is continuous (or not continuous). Let's explore ways to figure out if a function is continuous!
Defining Continuity
A function f(x) is continuous at a specific point 'c' in its domain if the following three conditions are met:
1️⃣ f(c) is defined (i.e., there is a value of the function at c)
2️⃣ The limit of the function as x approaches c exists
3️⃣ The value of the function at c (f(c)) is equal to the limit of the function as x approaches c. In other words, .
Defining Continuity With A Graph
To prove that a line is continuous at a specific point using a graph, you'll need to ensure that there are no jumps, gaps, or breaks in the graph at that point. The key is to visually demonstrate that the line flows smoothly without any interruptions. Here's how you can do it:
- 📈 Plot the Graph: Start by plotting the graph of the line. Make sure it's accurate and well-drawn.
- 🤓 Focus on the Point of Interest: Identify the specific point at which you want to prove continuity.
- ⛳ Check for a Continuous Connection: Examine the graph very closely as you approach the point from both the left and the right sides. Make sure that the line doesn't have any sudden jumps or holes.
- If the line connects smoothly as you get closer to the point from both sides, it's a sign of continuity.
- If there's a noticeable gap, jump, or any kind of interruption in the graph at that point, it's not continuous.
- 🏷️ Use Labels and Annotations: To make your case clear, you can label the point in question and perhaps mark the paths approaching it from both sides. You might also annotate the graph with a note like "Continuous at this point" or "Discontinuous at this point" to highlight your conclusion.
- 🤯 Provide an Explanation: Alongside the graph, explain why the line is continuous at that point. For example, you can state that the value of the function at the point matches the limit from both directions. Alternatively, if it's discontinuous, explain the specific reason for the discontinuity.
Examples: Defining Continuity in Graphs
For example, take a look at these graphs:

Image courtesy of SFU.ca
In this example, only the top left graph is continuous. On all other graphs, there is a skip which makes the graph discontinuous at that point. Below the graphs are explanations as to why the graph is not continuous. These explanations are what we should aim for!
Defining Continuity: Practice Questions
Defining Continuity: Question 1
Is the function continuous at ? Justify your conclusion using the definition.
Explanation: To check continuity, we need to ensure three things:
- f(2) exists (It's 3 * 2 + 5 = 11, so it's a real number).
- The limit as x approaches 2 exists.
- The limit matches the value (limit = 11).
Defining Continuity: Question 2
Consider the functions and . Are both functions continuous at ? Justify your conclusions using the definition.
Explanation: For each function, apply the definition of continuity:
- Check if f(3) and g(3) are defined ( and ).
- Calculate the limits as x approaches 3 for both functions.
- For f(x), the limit as x approaches 3 is also 9 (matching ).
- For g(x), the limit as x approaches 3 is 6 (matching ).
Perfect, both functions are continuous at x = 3. ✏️
Defining Continuity: Question 3
Examine the functions and . Are both functions continuous at ? Justify your answer.
Explanation:
- Check if p(0) and q(0) are defined (, which is undefined, and , a real number).
- Calculate the limits as x approaches 0 for both functions.
- For p(x), the limit as x approaches 0 is undefined (division by zero), which doesn't match p(0).
- For q(x), the limit as x approaches 0 is 0, which matches q(0).
Therefore, function q(x) is continuous at x = 0, while p(x) is not continuous at x = 0.
Problem-Solving Tips
Good luck, you got this! 🍀

© 2024 Fiveable Inc. All rights reserved.