Browse By Unit
1.9 Connecting Multiple Representations of Limits
6 min read•june 18, 2024
1.9 Connecting Multiple Representations of Limits
Throughout this unit, we’ve learned how to determine (or estimate) limits from different kinds of representations, including graphs, tables, and algebraic expressions. In this topic, we’ll practice connecting these various representations.
📈Connecting Multiple Representations of Limits
To connect the numerical, graphical, and algebraic representations of limits, we have to be able to gain information from each representation individually and then figure out how the information corresponds or corroborates with each other. This will allow us to gain a more complete understanding of the behavior of the function as x approaches the limit.
For example, we can use the numerical representation to approximate the limit, and then confirm our answer by observing the graphical representation and/or determining the exact limit using the algebraic representation. Or vice versa! 🔂
An important point to note is that sometimes one representation may be more informative than the others. For example, a function that is difficult to manipulate algebraically can be graphed to understand the behavior of the function as x approaches the limit.
Here’s a quick review of each of these:
- 🔢 Numerical Representation - This is the most common method used to determine limits and involves plugging in different values of x that are close to the limit and seeing what the approaches. This data is presented in a table and gives us an approximation of the limit, not the exact solution.
- 📊 Graphical Representation - This method involves and observing the behavior of the as x approaches the limit. This method is also not an exact solution.
- 📝 Algebraic Representation - This involves using algebraic manipulation to determine the exact solution for the limit. With this, you may factor, rationalize denominators, or work with trig!
Now let’s give a question a try!
✏️ Multiple Representations of Limits: Walkthrough
Let be a function where . Which of the following could represent ?
Option A)
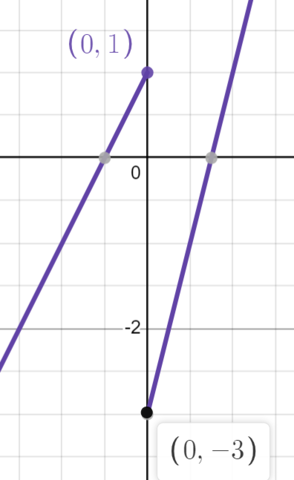
Image Courtesy of Desmos
Note: The graph has a removable discontinuity at . We’ll talk about this more in the next key topic.
Option B)
| -0.2 | -0.1 | -0.001 | 0.001 | 0.1 | 0.2 | |
| 1.04 | 1.01 | 1.000001 | 1.000001 | 1.01 | 1.04 |
Option C)
How can we tackle this problem? Well, we can look through the different options and evaluate the for each one and see if it equals . You essentially want to act like each option is on its own so you don’t get distracted by the others! 👀
📈 First, let’s take a look at the graph in a). We see that approaches as approaches from the left, but approaches and as approaches from the right. Therefore, a) is not the correct answer.
🔢 Next, if we look at the table in b), we see that as the values of approach on both the left and right sides, the values of approach , so the function depicted in b) could represent .
🤔 To confirm that b) is the correct answer, we can look at the function given in c). For values approaching on the left we see that approaches or , and for values approaching on the right we see that is . Since only one side approaches , is not equal to .
Therefore, b) is the correct answer.
📝 Limits Practice Problem
Now it’s time for you to do some practice on your own! 🔍
❓Limits Practice Question
Let be a function where . Which of the following could represent ?
a)
b)
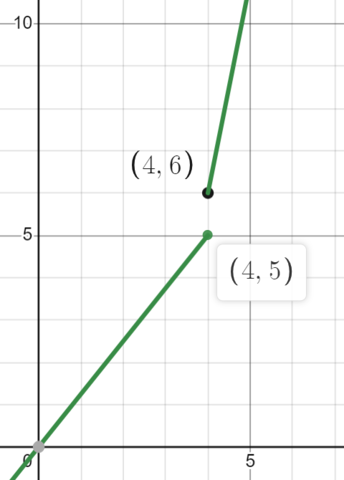
Image Courtesy of Desmos
c)
| 3.8 | 3.9 | 3.999 | 4 | 4.001 | 4.01 | 4.02 | |
| 6.2 | 6.01 | 6.001 | 4 | 4.999 | 4.9 | 4.8 |
✅ Limits Practice Solution
To solve this problem we can look through the answer choices and evaluate the for each one and see if it equals .
First, if we look at the equation in a), we see that we can algebraically manipulate it to be
Since we’re interested in the behavior of the function as approaches 4, we only care about the part of the function where .
Plugging in gets us , so a) is the correct answer.
To confirm that a) is the correct answer, we can look at both the graph in b) and the table in c).
We see that while the graph in b) depicts approaching as approaches from the left, approaches and not as approaches from the right. Therefore, b) is not the correct answer.
From the table in c), we see that for values approaching on the left, approaches , and for values approaching on the right, approaches . Since only one side approaches , is not equal to .
Therefore, a) is the correct answer.
⭐ Closing
Nice work! This key topic is really all about combining what you’re learned so far about limits. On the AP, they’ll likely ask you to do this more than practicing the skills individually.
<< Hide Menu
1.9 Connecting Multiple Representations of Limits
6 min read•june 18, 2024
1.9 Connecting Multiple Representations of Limits
Throughout this unit, we’ve learned how to determine (or estimate) limits from different kinds of representations, including graphs, tables, and algebraic expressions. In this topic, we’ll practice connecting these various representations.
📈Connecting Multiple Representations of Limits
To connect the numerical, graphical, and algebraic representations of limits, we have to be able to gain information from each representation individually and then figure out how the information corresponds or corroborates with each other. This will allow us to gain a more complete understanding of the behavior of the function as x approaches the limit.
For example, we can use the numerical representation to approximate the limit, and then confirm our answer by observing the graphical representation and/or determining the exact limit using the algebraic representation. Or vice versa! 🔂
An important point to note is that sometimes one representation may be more informative than the others. For example, a function that is difficult to manipulate algebraically can be graphed to understand the behavior of the function as x approaches the limit.
Here’s a quick review of each of these:
- 🔢 Numerical Representation - This is the most common method used to determine limits and involves plugging in different values of x that are close to the limit and seeing what the approaches. This data is presented in a table and gives us an approximation of the limit, not the exact solution.
- 📊 Graphical Representation - This method involves and observing the behavior of the as x approaches the limit. This method is also not an exact solution.
- 📝 Algebraic Representation - This involves using algebraic manipulation to determine the exact solution for the limit. With this, you may factor, rationalize denominators, or work with trig!
Now let’s give a question a try!
✏️ Multiple Representations of Limits: Walkthrough
Let be a function where . Which of the following could represent ?
Option A)

Image Courtesy of Desmos
Note: The graph has a removable discontinuity at . We’ll talk about this more in the next key topic.
Option B)
| -0.2 | -0.1 | -0.001 | 0.001 | 0.1 | 0.2 | |
| 1.04 | 1.01 | 1.000001 | 1.000001 | 1.01 | 1.04 |
Option C)
How can we tackle this problem? Well, we can look through the different options and evaluate the for each one and see if it equals . You essentially want to act like each option is on its own so you don’t get distracted by the others! 👀
📈 First, let’s take a look at the graph in a). We see that approaches as approaches from the left, but approaches and as approaches from the right. Therefore, a) is not the correct answer.
🔢 Next, if we look at the table in b), we see that as the values of approach on both the left and right sides, the values of approach , so the function depicted in b) could represent .
🤔 To confirm that b) is the correct answer, we can look at the function given in c). For values approaching on the left we see that approaches or , and for values approaching on the right we see that is . Since only one side approaches , is not equal to .
Therefore, b) is the correct answer.
📝 Limits Practice Problem
Now it’s time for you to do some practice on your own! 🔍
❓Limits Practice Question
Let be a function where . Which of the following could represent ?
a)
b)

Image Courtesy of Desmos
c)
| 3.8 | 3.9 | 3.999 | 4 | 4.001 | 4.01 | 4.02 | |
| 6.2 | 6.01 | 6.001 | 4 | 4.999 | 4.9 | 4.8 |
✅ Limits Practice Solution
To solve this problem we can look through the answer choices and evaluate the for each one and see if it equals .
First, if we look at the equation in a), we see that we can algebraically manipulate it to be
Since we’re interested in the behavior of the function as approaches 4, we only care about the part of the function where .
Plugging in gets us , so a) is the correct answer.
To confirm that a) is the correct answer, we can look at both the graph in b) and the table in c).
We see that while the graph in b) depicts approaching as approaches from the left, approaches and not as approaches from the right. Therefore, b) is not the correct answer.
From the table in c), we see that for values approaching on the left, approaches , and for values approaching on the right, approaches . Since only one side approaches , is not equal to .
Therefore, a) is the correct answer.
⭐ Closing
Nice work! This key topic is really all about combining what you’re learned so far about limits. On the AP, they’ll likely ask you to do this more than practicing the skills individually.

© 2024 Fiveable Inc. All rights reserved.