Browse By Unit
1.12 Confirming Continuity over an Interval
3 min read•june 18, 2024
1.12 Confirming Continuity over an Interval
Welcome back to AP Calculus with Fiveable! This topic focuses on continuity over an interval. We’ve worked through determining limits from both graphs, equations and different types of discontinuities, so let's combine all of the skills we've learned so far. 🙌
📈 Continuity on an Interval
The College Board AP Calculus Exam description states, “A function is continuous on an interval if the function is continuous at each point in the interval.”
This means that as long as the function’s domain is continuous, then the function will be continuous. You can quickly identify discontinuities on a graph by looking for holes, jumps, and other breaks. If you can draw your graph as a single stroke without gaps, your function is continuous! ✏️
College Board reminds us that “polynomial, rational, power, exponential, logarithmic, and trigonometric functions are continuous on all points in their domains.” For instance, a log function such as will be continuous at all points in its domain (0,∞).
🏁 Continuity for Piecewise Functions
Continuity over intervals is key for piecewise functions! We can check the domain for each piece, and make sure to confirm continuity at the point when the function changes expressions.
⛳ Checking Domain Restrictions
Some common domain restrictions we need to check are square roots and denominators of rational functions. 🚩
For square roots, , since we cannot take the square root of an imaginary number.
For example looks like the following. Since the expression under the square root, . As you can see, the graph has a domain of .
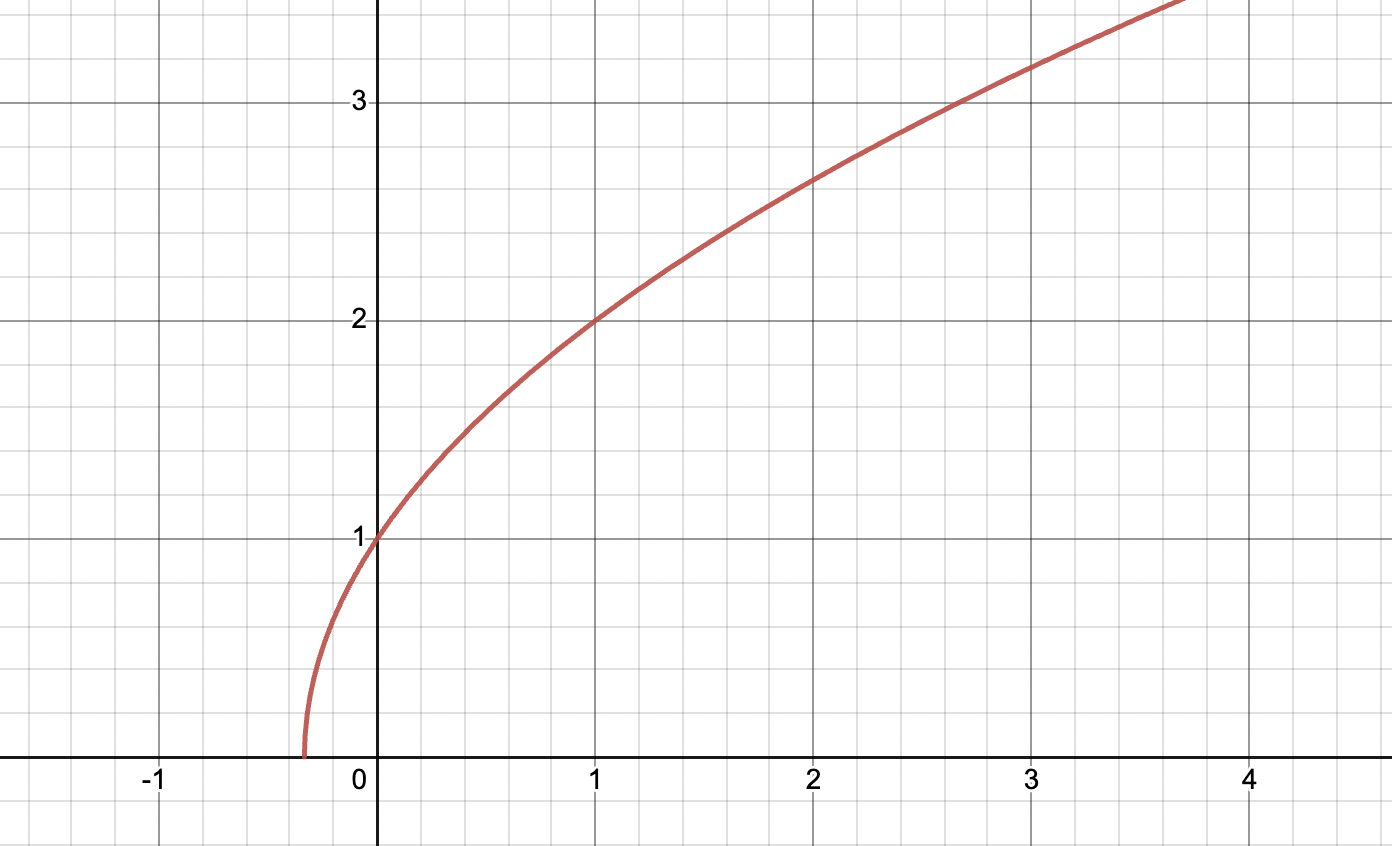
Graph created with Desmos
For rational functions, , because we cannot divide by 0.
For example, looks like the following. Since the denominator cannot equal 0, . The domain of this graph is .

Graph created with Desmos
We already learned to confirm continuity at a single point in Topic 1.11: Confirming Continuity at a Point! As a review, make sure the limits approach the same value on both sides. The left-hand limit should be equal to the right-hand limit, which should equal the value of the function at the point x = a.
🧮 Practice Problems
Let’s work on a few questions and make sure we have the concept down!
1) Continuity of a Piecewise Function
Given the following piecewise function, determine if the function is continuous on the interval .
👉 Step 1: Check for Discontinuities in the Domains
First, let's check for discontinuities in the domains of both of the expressions. Because both of the expressions are polynomials, they will be continuous throughout their domains.
👉 Step 2: Check Continuity at the Point the Function Changes Expressions
The next thing we have to check is the point where the function changes expressions, x = 3.
At x = 3, the left-hand limit .
The right hand limit
And finally, . Therefore the function is continuous at x = 3.
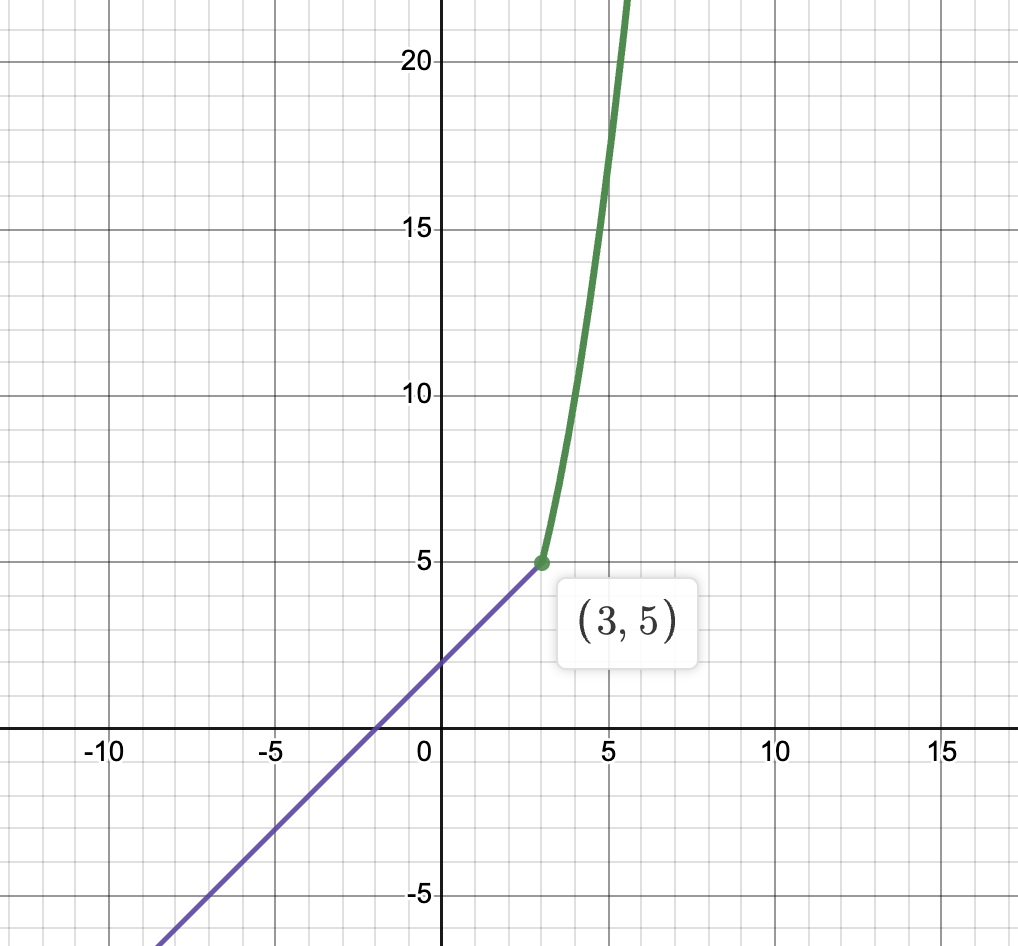
Graph created with Desmos
👉 Step 3: Answering the Question
Since we checked all possible discontinuities, we can now say that the function is continuous on the interval . Great work! 👍
2) Continuity of Rational Function
Determine if the following function is continuous on the interval .
For this function, we need to first check any discontinuities in the domain.
Since this is a rational function, the denominator cannot equal 0. Therefore, the domain of the function is , since x = -2 would cause the denominator to equal zero. This proves that there is a vertical asymptote here!
But that means the function is not continuous on the interval from because x = -2 is not included in its domain.
Check it out in the graph!
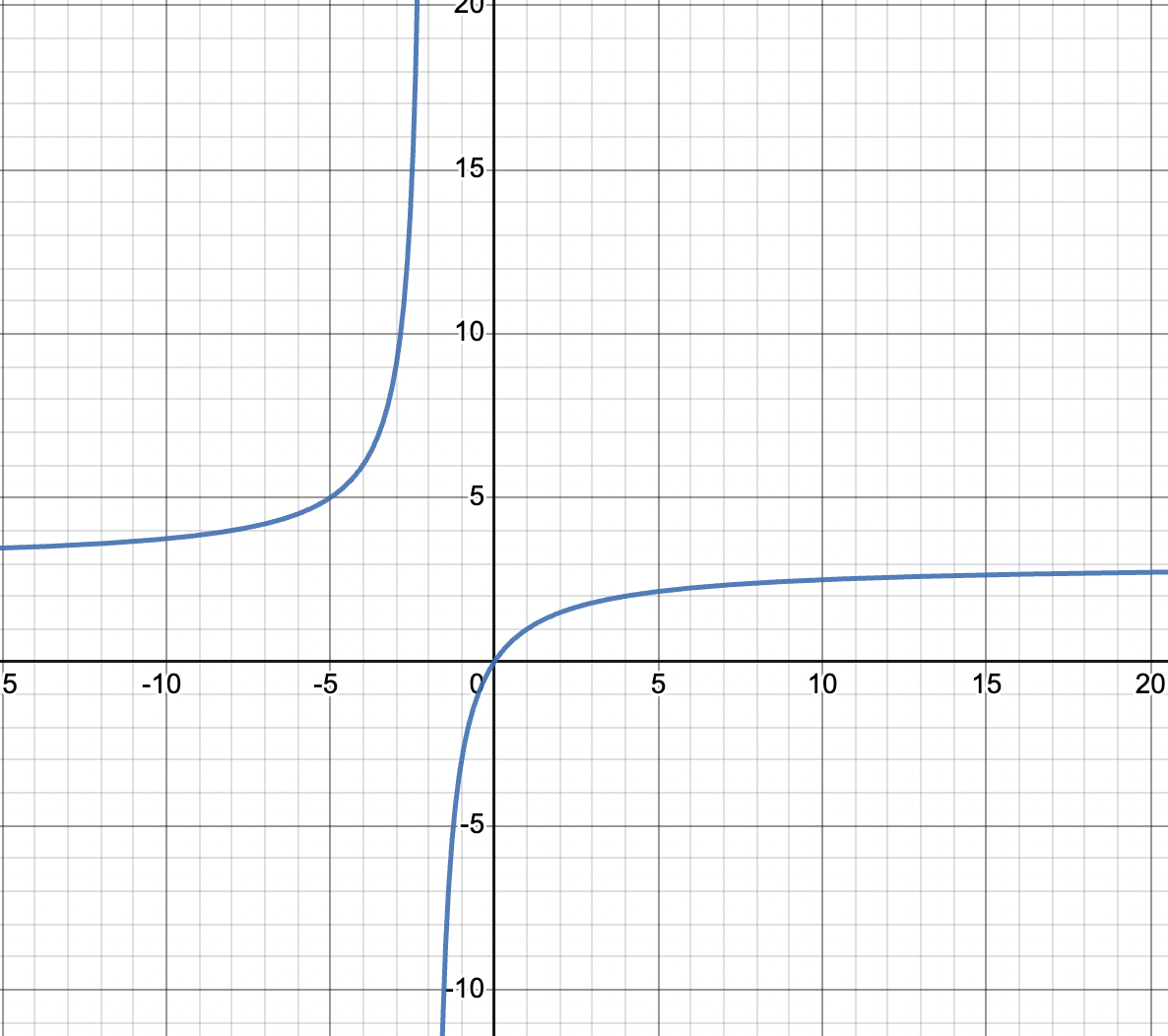
Image created with Desmos
🌟 Closing
Nice work! Confirming continuity over an interval is a key foundational topic for AP Calculus. You can anticipate encountering these types of questions on the exam, both in multiple-choice and as part of a free response.

Image Courtesy of Giphy
<< Hide Menu
1.12 Confirming Continuity over an Interval
3 min read•june 18, 2024
1.12 Confirming Continuity over an Interval
Welcome back to AP Calculus with Fiveable! This topic focuses on continuity over an interval. We’ve worked through determining limits from both graphs, equations and different types of discontinuities, so let's combine all of the skills we've learned so far. 🙌
📈 Continuity on an Interval
The College Board AP Calculus Exam description states, “A function is continuous on an interval if the function is continuous at each point in the interval.”
This means that as long as the function’s domain is continuous, then the function will be continuous. You can quickly identify discontinuities on a graph by looking for holes, jumps, and other breaks. If you can draw your graph as a single stroke without gaps, your function is continuous! ✏️
College Board reminds us that “polynomial, rational, power, exponential, logarithmic, and trigonometric functions are continuous on all points in their domains.” For instance, a log function such as will be continuous at all points in its domain (0,∞).
🏁 Continuity for Piecewise Functions
Continuity over intervals is key for piecewise functions! We can check the domain for each piece, and make sure to confirm continuity at the point when the function changes expressions.
⛳ Checking Domain Restrictions
Some common domain restrictions we need to check are square roots and denominators of rational functions. 🚩
For square roots, , since we cannot take the square root of an imaginary number.
For example looks like the following. Since the expression under the square root, . As you can see, the graph has a domain of .

Graph created with Desmos
For rational functions, , because we cannot divide by 0.
For example, looks like the following. Since the denominator cannot equal 0, . The domain of this graph is .

Graph created with Desmos
We already learned to confirm continuity at a single point in Topic 1.11: Confirming Continuity at a Point! As a review, make sure the limits approach the same value on both sides. The left-hand limit should be equal to the right-hand limit, which should equal the value of the function at the point x = a.
🧮 Practice Problems
Let’s work on a few questions and make sure we have the concept down!
1) Continuity of a Piecewise Function
Given the following piecewise function, determine if the function is continuous on the interval .
👉 Step 1: Check for Discontinuities in the Domains
First, let's check for discontinuities in the domains of both of the expressions. Because both of the expressions are polynomials, they will be continuous throughout their domains.
👉 Step 2: Check Continuity at the Point the Function Changes Expressions
The next thing we have to check is the point where the function changes expressions, x = 3.
At x = 3, the left-hand limit .
The right hand limit
And finally, . Therefore the function is continuous at x = 3.

Graph created with Desmos
👉 Step 3: Answering the Question
Since we checked all possible discontinuities, we can now say that the function is continuous on the interval . Great work! 👍
2) Continuity of Rational Function
Determine if the following function is continuous on the interval .
For this function, we need to first check any discontinuities in the domain.
Since this is a rational function, the denominator cannot equal 0. Therefore, the domain of the function is , since x = -2 would cause the denominator to equal zero. This proves that there is a vertical asymptote here!
But that means the function is not continuous on the interval from because x = -2 is not included in its domain.
Check it out in the graph!

Image created with Desmos
🌟 Closing
Nice work! Confirming continuity over an interval is a key foundational topic for AP Calculus. You can anticipate encountering these types of questions on the exam, both in multiple-choice and as part of a free response.

Image Courtesy of Giphy

© 2024 Fiveable Inc. All rights reserved.