Browse By Unit
What is implicit differentiation and how do I do it?
1 min read•july 11, 2024
Explicit vs. Implicit Differentiation
By now, you've probably covered basic differentiation of a function y in terms of a single variable x. This is called explicit differentiation.
Implicit differentiation, on the other hand, is differentiating a variable in terms of another variable. We're not just taking the derivative of x or 8x+6 anymore, we're taking the derivative of whole equations like y = 8x+6 to find dy/dx.
Need a quick review on taking and finding derivatives, make sure you watch this 🎥 video introducing and explaining derivatives for a refresher.
Explicit Differentiation
- Single variable function/relation
Example:
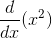
Implicit Differentiation
- More than one variable in the function/relation
Example:
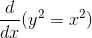
So how do you do implicit differentiation? Just apply the chain rule!
🌟 Example:
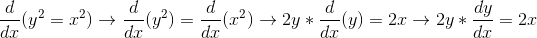
We can even simplify further to solve for dy/dx!
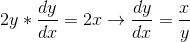
...And there you have it!
Implicit differentiation is useful in solving differential equations, where you'll need to solve for dy/dx. Some applications include optimization, e.g. finding the rate of change of volume with respect to the rate of change of time.
For more examples and help watch this video about 🎥 implicit differentiation and derivatives.
-----
<< Hide Menu
What is implicit differentiation and how do I do it?
1 min read•july 11, 2024
Explicit vs. Implicit Differentiation
By now, you've probably covered basic differentiation of a function y in terms of a single variable x. This is called explicit differentiation.
Implicit differentiation, on the other hand, is differentiating a variable in terms of another variable. We're not just taking the derivative of x or 8x+6 anymore, we're taking the derivative of whole equations like y = 8x+6 to find dy/dx.
Need a quick review on taking and finding derivatives, make sure you watch this 🎥 video introducing and explaining derivatives for a refresher.
Explicit Differentiation
- Single variable function/relation
Example:
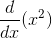
Implicit Differentiation
- More than one variable in the function/relation
Example:
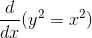
So how do you do implicit differentiation? Just apply the chain rule!
🌟 Example:
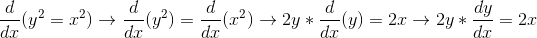
We can even simplify further to solve for dy/dx!
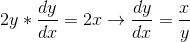
...And there you have it!
Implicit differentiation is useful in solving differential equations, where you'll need to solve for dy/dx. Some applications include optimization, e.g. finding the rate of change of volume with respect to the rate of change of time.
For more examples and help watch this video about 🎥 implicit differentiation and derivatives.
-----

© 2024 Fiveable Inc. All rights reserved.