Browse By Unit
Unit 2 Review - Differentiation: Definition & Fundamental Properties
7 min read•july 11, 2024
Defining Average and Instantaneous Rates of Change at a Point 📍
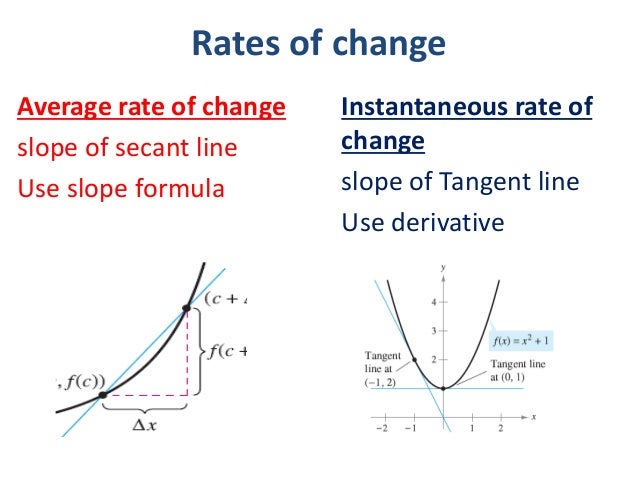
(Photo courtesy of slideshare.net)
An important concept to grasp in this lesson is the difference between the average rate of change and the instantaneous rate of change. The average rate of change is simply the slope of the secant line between two points. The instantaneous rate of change is the slope of the tangent line at any given point (the derivative).
The rate of change formula (pictured below) is the slope of the secant line between two points. "f(b)" represents your y-value to your first point and "f(a)" represents your y-value to your second point, "b" and "a" are the corresponding x-values to those coordinates.
- The instantaneous rate of change formula (pictured below) is the slope of the tangent line at a given point. Many people are puzzled with f(x+h) but it simply means that whenever you see an x in your original equation, you insert "x+h." For example, if f(x) = x² + 3x - 9 then f(x+h) = (x+h)² + 3(x+h) - 9. The second part of this formula is subtracting f(x) from f(x+h); however, a common error is that students forget to distribute the "-" sign to all the terms in the original function. The last part is to put everything over h and simplify the entire equation by combining like terms and factoring). If there are any h terms left you evaluate them as 0 and then simplify.
-----
Defining the Derivative of a Function and Using Derivative Notation 🤓
🎥Watch - AP Calculus AB/BC: Limit Definition of a Derivative
The function that gives the instantaneous rate of change is the derivative, and the derivative is the slope of the tangent line to the graph at a given point. The formula for the derivative is the same as the instantaneous rate of change formula.
The AP exam loves using the notation for the derivative, so don't be scared as they all mean the same thing; however in certain scenarios in calculus, we may use one notation over the other. Here are some of the ways we can express the derivative (pictured below). For now, only review the notations concerning the first derivative. The bottom line is that y' is synonymous with f'(x) or dy/dx or d/dx f(x)!

(Photo courtesy of education.fcps.org)
Connecting Differentiability and Continuity: Determining when Derivatives DO or DO NOT EXIST ❗
🎥Read- AP Calculus AB/BC: Differentiability Rules
If you need a complete refresher on continuity you can watch a replay of our stream on Continuity here!
Being differentiable means that a derivative exists. It is important to know that being differentiable is being continuous however being continuous does not mean you are differentiable.
On top of being continuous in order to be differentiable, the function must have NO corners, cusps, and no vertical tangent lines.
Applying the Power Rule 🦸♂️🦸♀️
⚡ Watch- AP Calculus AB/BC: Practicing Derivative Rules
Using the definition of the derivative for every single problem you encounter is a time-consuming and it is also open to careless errors and mistakes. However, one great mathematician decided to bless us with a fundamental rule known as the Power Rule, pictured below.
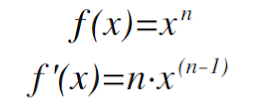
- Your "n" term is the power your x-term is being raised to.
For example, in x² your "n" term would be 2. Additionally, you multiply that "n" value to the term's coefficient (in x² your coefficient is 1) and then decrease your terms exponent by 1 (using the power rule the derivative of x² is 2x).
- Remember: the derivative is the slope of the line tangent to any point on the graph and using the power rule (like the definition of the derivative) simply gives you the formula to the slope of the line tangent. If you would like to know what that point is then you would have to evaluate using your x-coordinate.
Derivative Rules: Constant, Sum, Difference, and Constant Multiple ➕➖
⚡ Watch- AP Calculus AB/BC: Introduction to Finding Derivatives
These first set of derivative rules are simple but absolutely crucial to your understanding of calculus.

(Photo courtesy of www.khanacademy.org)
- The sum rule states that the derivative of a sum of functions is the same as the sum of their derivatives.- Just like the sum rule, the difference rule states the derivative of a difference in functions is the same as the difference in their derivatives.
While these two rules may seem confusing, they are actually straightforward. The sum and difference rules are essentially applications of the power rule to every term, as well as combining them (if possible). Here is an example of using both these formulas, pictured below:
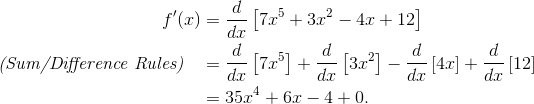
(Photo courtesy of https://magoosh.com)
- The constant multiple rule states that the derivative of a constant times a function is equal to the constant times the derivative.
For example, the derivative of 5・x², (5x²) is equal to 5 times the derivative of 2x.
- The constant rule states that the derivative of any constant is 0 (for example, the derivative of 5 is 0).
Derivatives of cos, sin, natural exponential functions, and the natural log 🤔
⚡ Read- AP Calculus AB/BC: Deritvatives of Special Functions
These rules must be committed to memory as they are used throughout the year in calculus.
-
- The derivative of sin (x) is cos (x).- The derivative of cos (x) is -sin (x).
If you would like to find a derivative of a trig function with a constant (such as 5sin(x)), you would use the constant multiple rule to get 5cos(x).
-
- It is important to note that the derivative of these functions only work when you are only using "x" in the function. For example, the derivative of sin(3x) is not cos(3x), in order to get the correct derivative you would need to apply the chain rule. (Do not worry about the chain rule in this unit as it is covered in Unit 3 of calculus.) The derivative of e^x is e^x. No matter how many times you take the derivative of this function, the derivative of e^x will remain as e^x.
-
The derivative of e^x only works when it is raised to only the "x" power. For example, the derivative e^2x is not e^2x, in order to get the correct derivative you would need to apply the chain rule.
The derivative of ln(x) is pictured below. If you would want to find the derivative of ln(4x), you would need to apply the chain rule.
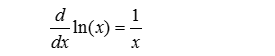
The Product Rule ✖
By now, we know how to add and subtract derivative functions, but what about multiplying them? With the product rule we can finally multiply derivatives together. Here is the rule (pictured below)

f(x) and g(x) represent two different functions that are being multiplied together. Here is an example of how to apply this rule (pictured below).
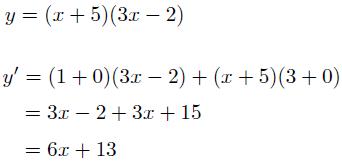
(Photo courtesy of need2knowaboutcalculus.weebly.com)
Let's call the first function f(x) and the second function g(x). For our first part, we will take the derivative of the first function and multiply it by the original second function. For the second part, we then multiply the original first function and multiply that by the derivative of the second function. Finally, we will add up both parts.
If it is helpful to remember the derivative of first times second plus derivative of second times first, go for it!
The Quotient Rule ➗
Let's now move on to the product rule's partner: the Quotient Rule! With the quotient rule, we can finally divide derivatives. Here is what the quotient rule looks like. pictured below:
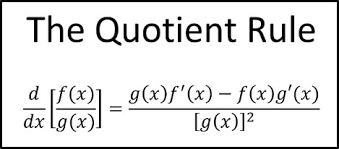
(Photo courtesy of andymath.com)
The quotient rule states that f(x) is the top function (the dividend) and g(x) is the bottom function (divisor). The first part would be to multiply g(x) by the derivative of f(x) and the second part would be to multiply f(x) by the derivative of g(x). After that, you would subtract the two parts (don't forget to distribute the negative sign!). Lastly, you would divide everything by g(x)². If you need another visual, here is an example (pictured below).
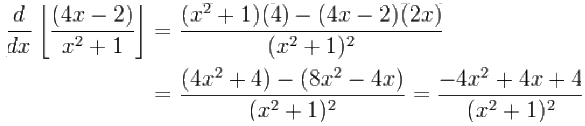
(Photo courtesy of www.studygeek.org)
Note that (4x-2) is your top function, f(x) and (x²+1) is your bottom function, g(x).
Finding the Derivatives of Tangent, Cotangent, Secant, and/or Cosecant Functions 🔎
⚡ Read- AP Calculus AB/BC: Deritvatives of Special Functions, Part II
Here is a helpful chart with the derivatives of the rest of the trigonometric functions besides sine and cosine:

(Photo courtesy of slideplayer.com)
However, it is important to take note that AP Calculus mainly focuses on the derivatives of sin, cos, and tan.
Final Note 🎓
Make sure you get the basics down of unit 2 of AP Calculus AB for this unit sets the foundations of calculus, which is essentially the rest of the course. As a result, it is essential for you to understand these concepts!
<< Hide Menu
Unit 2 Review - Differentiation: Definition & Fundamental Properties
7 min read•july 11, 2024
Defining Average and Instantaneous Rates of Change at a Point 📍

(Photo courtesy of slideshare.net)
An important concept to grasp in this lesson is the difference between the average rate of change and the instantaneous rate of change. The average rate of change is simply the slope of the secant line between two points. The instantaneous rate of change is the slope of the tangent line at any given point (the derivative).
The rate of change formula (pictured below) is the slope of the secant line between two points. "f(b)" represents your y-value to your first point and "f(a)" represents your y-value to your second point, "b" and "a" are the corresponding x-values to those coordinates.
- The instantaneous rate of change formula (pictured below) is the slope of the tangent line at a given point. Many people are puzzled with f(x+h) but it simply means that whenever you see an x in your original equation, you insert "x+h." For example, if f(x) = x² + 3x - 9 then f(x+h) = (x+h)² + 3(x+h) - 9. The second part of this formula is subtracting f(x) from f(x+h); however, a common error is that students forget to distribute the "-" sign to all the terms in the original function. The last part is to put everything over h and simplify the entire equation by combining like terms and factoring). If there are any h terms left you evaluate them as 0 and then simplify.
-----
Defining the Derivative of a Function and Using Derivative Notation 🤓
🎥Watch - AP Calculus AB/BC: Limit Definition of a Derivative
The function that gives the instantaneous rate of change is the derivative, and the derivative is the slope of the tangent line to the graph at a given point. The formula for the derivative is the same as the instantaneous rate of change formula.
The AP exam loves using the notation for the derivative, so don't be scared as they all mean the same thing; however in certain scenarios in calculus, we may use one notation over the other. Here are some of the ways we can express the derivative (pictured below). For now, only review the notations concerning the first derivative. The bottom line is that y' is synonymous with f'(x) or dy/dx or d/dx f(x)!

(Photo courtesy of education.fcps.org)
Connecting Differentiability and Continuity: Determining when Derivatives DO or DO NOT EXIST ❗
🎥Read- AP Calculus AB/BC: Differentiability Rules
If you need a complete refresher on continuity you can watch a replay of our stream on Continuity here!
Being differentiable means that a derivative exists. It is important to know that being differentiable is being continuous however being continuous does not mean you are differentiable.
On top of being continuous in order to be differentiable, the function must have NO corners, cusps, and no vertical tangent lines.
Applying the Power Rule 🦸♂️🦸♀️
⚡ Watch- AP Calculus AB/BC: Practicing Derivative Rules
Using the definition of the derivative for every single problem you encounter is a time-consuming and it is also open to careless errors and mistakes. However, one great mathematician decided to bless us with a fundamental rule known as the Power Rule, pictured below.
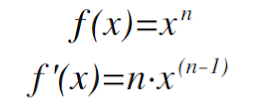
- Your "n" term is the power your x-term is being raised to.
For example, in x² your "n" term would be 2. Additionally, you multiply that "n" value to the term's coefficient (in x² your coefficient is 1) and then decrease your terms exponent by 1 (using the power rule the derivative of x² is 2x).
- Remember: the derivative is the slope of the line tangent to any point on the graph and using the power rule (like the definition of the derivative) simply gives you the formula to the slope of the line tangent. If you would like to know what that point is then you would have to evaluate using your x-coordinate.
Derivative Rules: Constant, Sum, Difference, and Constant Multiple ➕➖
⚡ Watch- AP Calculus AB/BC: Introduction to Finding Derivatives
These first set of derivative rules are simple but absolutely crucial to your understanding of calculus.

(Photo courtesy of www.khanacademy.org)
- The sum rule states that the derivative of a sum of functions is the same as the sum of their derivatives.- Just like the sum rule, the difference rule states the derivative of a difference in functions is the same as the difference in their derivatives.
While these two rules may seem confusing, they are actually straightforward. The sum and difference rules are essentially applications of the power rule to every term, as well as combining them (if possible). Here is an example of using both these formulas, pictured below:
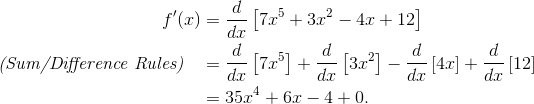
(Photo courtesy of https://magoosh.com)
- The constant multiple rule states that the derivative of a constant times a function is equal to the constant times the derivative.
For example, the derivative of 5・x², (5x²) is equal to 5 times the derivative of 2x.
- The constant rule states that the derivative of any constant is 0 (for example, the derivative of 5 is 0).
Derivatives of cos, sin, natural exponential functions, and the natural log 🤔
⚡ Read- AP Calculus AB/BC: Deritvatives of Special Functions
These rules must be committed to memory as they are used throughout the year in calculus.
-
- The derivative of sin (x) is cos (x).- The derivative of cos (x) is -sin (x).
If you would like to find a derivative of a trig function with a constant (such as 5sin(x)), you would use the constant multiple rule to get 5cos(x).
-
- It is important to note that the derivative of these functions only work when you are only using "x" in the function. For example, the derivative of sin(3x) is not cos(3x), in order to get the correct derivative you would need to apply the chain rule. (Do not worry about the chain rule in this unit as it is covered in Unit 3 of calculus.) The derivative of e^x is e^x. No matter how many times you take the derivative of this function, the derivative of e^x will remain as e^x.
-
The derivative of e^x only works when it is raised to only the "x" power. For example, the derivative e^2x is not e^2x, in order to get the correct derivative you would need to apply the chain rule.
The derivative of ln(x) is pictured below. If you would want to find the derivative of ln(4x), you would need to apply the chain rule.
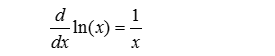
The Product Rule ✖
By now, we know how to add and subtract derivative functions, but what about multiplying them? With the product rule we can finally multiply derivatives together. Here is the rule (pictured below)

f(x) and g(x) represent two different functions that are being multiplied together. Here is an example of how to apply this rule (pictured below).
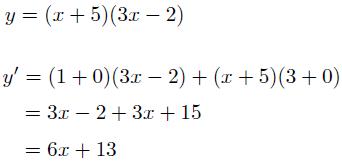
(Photo courtesy of need2knowaboutcalculus.weebly.com)
Let's call the first function f(x) and the second function g(x). For our first part, we will take the derivative of the first function and multiply it by the original second function. For the second part, we then multiply the original first function and multiply that by the derivative of the second function. Finally, we will add up both parts.
If it is helpful to remember the derivative of first times second plus derivative of second times first, go for it!
The Quotient Rule ➗
Let's now move on to the product rule's partner: the Quotient Rule! With the quotient rule, we can finally divide derivatives. Here is what the quotient rule looks like. pictured below:
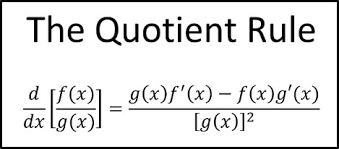
(Photo courtesy of andymath.com)
The quotient rule states that f(x) is the top function (the dividend) and g(x) is the bottom function (divisor). The first part would be to multiply g(x) by the derivative of f(x) and the second part would be to multiply f(x) by the derivative of g(x). After that, you would subtract the two parts (don't forget to distribute the negative sign!). Lastly, you would divide everything by g(x)². If you need another visual, here is an example (pictured below).
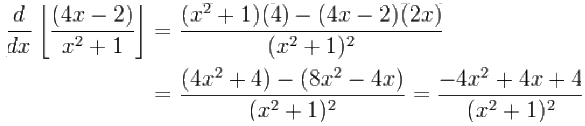
(Photo courtesy of www.studygeek.org)
Note that (4x-2) is your top function, f(x) and (x²+1) is your bottom function, g(x).
Finding the Derivatives of Tangent, Cotangent, Secant, and/or Cosecant Functions 🔎
⚡ Read- AP Calculus AB/BC: Deritvatives of Special Functions, Part II
Here is a helpful chart with the derivatives of the rest of the trigonometric functions besides sine and cosine:

(Photo courtesy of slideplayer.com)
However, it is important to take note that AP Calculus mainly focuses on the derivatives of sin, cos, and tan.
Final Note 🎓
Make sure you get the basics down of unit 2 of AP Calculus AB for this unit sets the foundations of calculus, which is essentially the rest of the course. As a result, it is essential for you to understand these concepts!

© 2024 Fiveable Inc. All rights reserved.